Using Rectangles to Find the Area of a Parallelogram

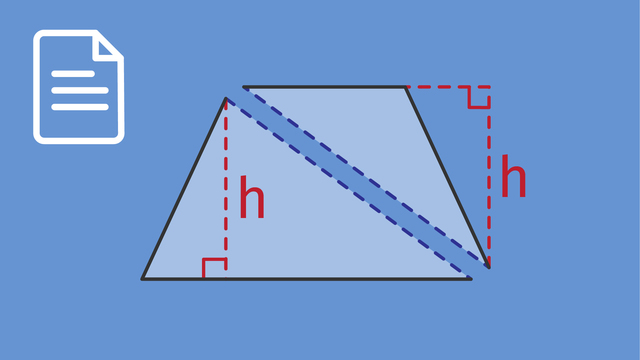
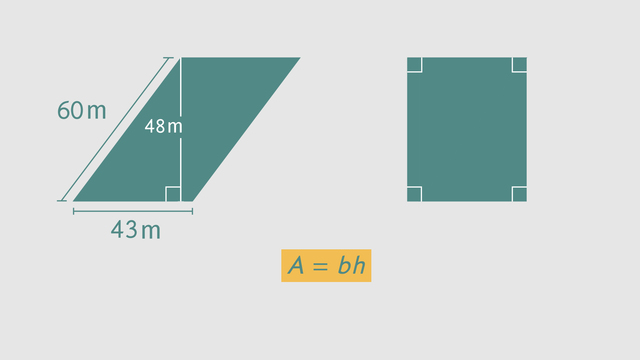
The mayor of Polygon, Pennsylvania is launching a "Revitalize the City" campaign to engage people in projects that make their city a better place to live. Today, she's meeting with a citizen who has a reputation for his "back to nature" approach to urban planning. He proposes to transform some of the city's empty lots into beautiful public parks by using rectangles to find the area of parallelograms. Before the landscaping project begins, we need to know the area of each vacant lot that will be rejuvinated. This underdeveloped plot of land is shaped like a parallelogram. A parallelogram is a type of quadrilateral. You may recall that the "quad" in quadrilateral means 4, which is how many sides these shapes have. As the name "parallelogram" suggests, both sets of its sides are parallel. What do you remember about parallel lines? Well, for one thing, if you extend them forever they will never intersect. You already know one kind of parellelogram a rectangle. It's a four-sided shape, with two sets of parallel sides. So what makes rectangles special? In a rectangle, all the interior angles are right angles which is indicated by this right angle symbol here. Now that we know a bit more about it, let's take a look at the exact dimensions of our parallelogram. One set of sides measures 50 meters across. The other sides are 40 meters. This line is 30 meters, and it measures the height. We know this is the height, because it's perpendicular with one of the sides. Perpendicular means they meet at a right angle, which again is indicated by this right angle symbol. The side that forms a right angle with our height is called the base. So we want to figure out the area of this shape. You already know how to find the area of rectangles. Let's see if we can find a way to use that knowledge here. Imagine breaking down our parallelogram into smaller, more familiar shapes. What shapes can you imagine creating? This process of breaking apart a shape is called decomposition. Now, we can move the pieces around without changing the area of the parallelogram. Where could we place this piece, so we are left with one large shape whose area we know how to calculate? By moving this right triangle to the other side we can make a rectangle. Notice that it now has four right angles. This process is called composition, which just means putting things together. Now we can easily calculate the new park's area, by multiplying 50 meters times 30 meters. That gives us an area of 1,500 square meters. Notice that the numbers we multiplied to calculate the area were the base and height of our parallelogram. And we didn't even need the other set of sides! Think that will always be true? Let's find out with our next example which is another parallelogam-shaped lot. One set of parallel sides measures 60 meters the other sides are 43 meters and the height is 48 meters. Just like in our last example, we know this line measures the height, because it is perpendicular to the base. So how would you find the area of this parallelogram? In our last example, we calculated the area by multiplying the length of the base times the height. To see if that works again, first decompose the parallelogram into smaller shapes then use those shapes to compose a rectangle. It looks like the formula we found in the last example also applies to this parallelogram. We can use this formula to find the area of any parallelogram: area equals base times the height. Our base is 43 so is our height 48 or 60? Remember, the height of a parallelogram is perpendicular to the base. So our height is 48. Multiplying these numbers together gives us our area of 2,064 square meters. To review: All parallelograms, no matter their size and shape, can be decomposed and then composed into rectangles. You can calculate their area by multiplying the base times the height. The height tells us how tall the shape is, and it's always perpendicular to the base. So keep your eyes open for this symbol, when trying to determine a parallelogram's height. Back in Polygon, Pennsylvania, the mayor has decided to check in on how the park project is going. Yikes. I guess that eccentric citizen went a little bananas?