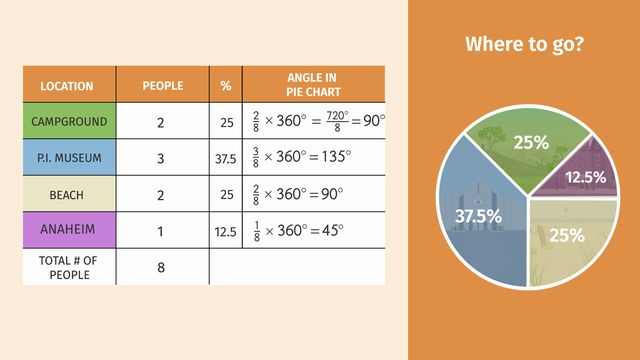
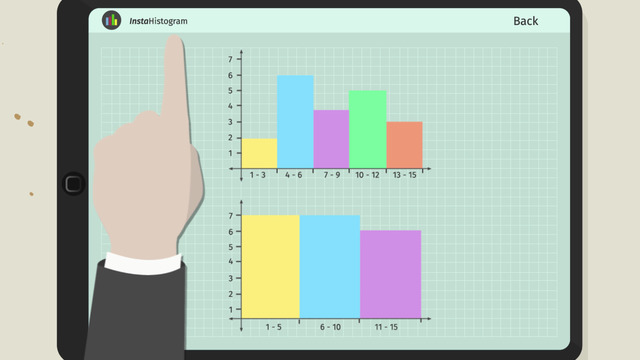
Stem and Leaf Plots

Stem and Leaf Plots exercise

• Explain how to create a stem and leaf plot.

  Hints

  You can check your stem and leaf plot by counting the leaves. This number must correspond to the number of data points.

  This is a possible key: 21 | 3 stands for 21.3.

  • 21 represents the stem.
  • 3 is a leaf.

  The advantage of a stem and leaf plot is that it's easy to create and to interpret.

  Solution

  How do we create a stem and leaf plot?

  First, we look for the smallest and largest numbers.

  Next, we create the stem: a vertical column listing the digits of each number excluding the right most number. Repeating numbers are listed just once.

  Last we add a leaf: list the last digit for every data point in descending order, noting that repeated data points are listed as often as they appear.

  We can check that the number of leaves corresponds with the number of all data points.

  For a better understanding, it's useful to write a key down.

• Create a stem and leaf plot.

  Hints

  The digits of the numbers excluding the most right, are listed starting with the lowest in the stem column. Each number is listed only once.

  The leaf column contains every right digit which appears for each steam value.

  The right digits are listed as often as they appear.

  Solution

  The solution can be seen here.

  The lowest number of the data set is $21.3$ and the highest one is $24.5$.

  So the numbers $21$ up to $24$ are listed in a stem column. Each number is listed only once, even if it appears more than one time.

  Next, the last digits are listed in the leaf column. They are listed as often as they appear.

• Find the right key.

  Hints

  The stem contains the digits of the numbers excluding the most right one.

  The digits most right are listed as leaves, and are listed as often as they appear.

  You can recognize the key by the original list of data.

  Solution

  To the right you see the stem and leaf plot for the example given in the video. Let's check the plots beginning with the first one:

  The data list is given by $\{$104, 111, 104, 121, 107, 112, 123, 123, 141, 148$\}$ with the key "10 | 4 means 104".

  Next, the middle plot: the data list is given by $\{$104, 105, 112, 113, 113, 121, 137, 142, 145$\}$ with the key "11 | 3 means 113".

  Last, we examine the lower plot: the data list is given by $\{$103, 103, 105, 111, 122, 124, 125, 133, 137, 144$\}$ with the key "12 | 2 means 122".

• Combine the data sets with the right stem and leaf plots.

  Hints

  First, you can count the number of leaves. This number must correspond to the number of elements in the data set.

  Compare the data in the plot with the given key of the data set.

  You can also rewrite all the information in the plot as a set of data.

  Solution

  How can we determine which plot belongs to the given data?

  There are different ways we can check which set of data belongs to which stem and leaf plot:

  • We count the number of leaves which appear in the stem and leaf plot, which must correspond to the number of data points in the list.
  • Looking at the key, we can recognize the kind of the data: whole numbers or decimal numbers.
  • We can check the data itself using the given key.

• Name the advantage of stem and leaf plots.

  Hints

  Try to create this stem and leaf plot on your own.

  You can check immediately, for example, that four elements belong to the first stem $21$.

  Solution

  Why should we create a stem and leaf plot?

  The advantages are the following:

  • This kind of plot is quick to made.
  • Whole numbers appear in this plot.
  • They are easier to interpret.

• Create a data set.

  Hints

  Pay attention to the key.

  Remember that repeating leafs give repeating data points.

  Let's have a look at the following example, with stem on the left and leaf on the right:

  • $3~~|~~4$ stands for 34 with the key "1 | 2 means 12".
  • $3~~|~~4$ stands for 3.4 with the key "1 | 2 means 1.2".
  • $3~~|~~4$ stands for 0.34 with the key "1 | 2 means 0.12".

  Solution

  Let's start with the first plot,

  $\begin{array}{c|l} \text{stem}&\text{leaf}\\ \hline 1&1~3~4~5\\ 2&1~1\\ 3&\\ 4&2~2\\ \end{array}$

  with the key "1 | 4 means 1.4"

  The corresponding data set is given by $\{$ 1.1, 1.3, 1.4, 1.5, 2.1, 2.1, 4.2, 4.2$\}$.

  Next, we have

  $\begin{array}{c|l} \text{stem}&\text{leaf}\\ \hline 1&4~4~5\\ 2&\\ 3&3~3~7\\ 4&1\\ \end{array}$

  with the key: "3 | 3 means 33". This plot corresponds to the following data set: $\{$14, 14, 15, 33, 33, 37, 41$\}$.

  Lastly, we have

  $\begin{array}{c|l} \text{stem}&\text{leaf}\\ \hline 23&1~1~4\\ 24&\\ 25&2~8 \end{array}$

  with the key: "23 | 1 means 2.31". This results in the data set $\{$2.31, 2.31, 2.34, 2.52. 2.58$\}$.