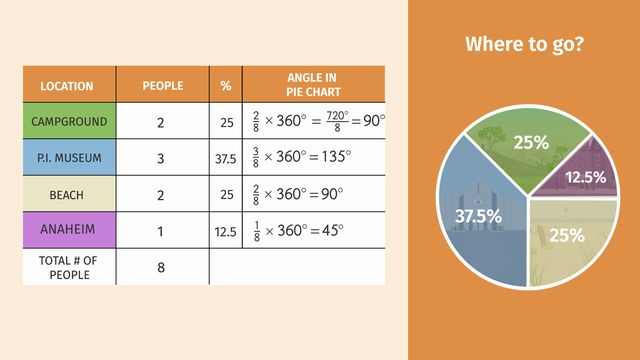
Frequency Tables

Frequency Tables exercise

• Name the different ways to represent data.

  Hints

  The graph of a quadratic function is a parabola.

  Here you see an example of a representation.

  Some representations improve the readability of data. So the data can be interpreted much easier.

  Solution

  Here you see one kind of representation of the number of times each animals burps: the frequency table.

  • The left-most column contains the names or pictures of the animals, and also of Dharma.
  • In the middle column we tally the frequencies.
  • In the right-most column the corresponding numbers are written down.

  There are two more representations which improve the readability of data:

  • The bar graph: the $y$-axis is labeled by frequency, while the $x$-axis is labeled by the different animals. The frequencies are shown as bars.
  • The dot plot: it looks a little bit like a bar graph. What's the difference? The frequencies are shown as dots. Sometimes it's a little bit harder to read, like if one dot represents two burps, for example.

• Find the right bar graph.

  Hints

  Pay attention to the $y$-axis; this is where the frequencies are labeled.

  Compare the frequencies you get from the bar graph with those given in the frequency table.

  The number of cow burps is the greatest of all the animals.

  Solution

  A bar graph is a graph that shows the distribution of data using bars to indicate frequency.

  The graph corresponding to the frequency table above can be seen to the right.

  The $y$-axis is labeled by the frequency. So you can determine the frequency belonging to each bar.

  The $x$-axis is labeled by pictures of the animals as well as Dharma.

• Find the right number of dots for the dot plot.

  Hints

  The number of dots for each pig corresponds to the number of apples that pig eats a day.

  Highlight the dots from bottom to top.

  Highlight two dots if the corresponding pig has eaten two apples.

  Solution

  Dot plots represent data in a coordinate system:

  • The $y$-axis is labeled by frequencies.
  • The $x$-axis is labeled by names or numbers or pictures. Here it is labeled by the pig names.

  For each pig, we plot as many dots from the bottom to the top as apples eaten.

  The resulting dot plot can be seen beside.

• Pair the right frequency tables with the right bar graphs.

  Hints

  Check the length of the bars for each item.

  You can determine the length of any bar by drawing a horizontal line, parallel to the $x$-axis. The length can be read by the intersection of this line with the $y$-axis.

  The length of each bar corresponds with the frequency of the corresponding item.

  Solution

  A bar graph is a graph that shows the distribution of data using bars to indicate frequency.

  The $y$-axis and $x$-axis of each bar graph are labeled as follows:

  • The $y$-axis is labeled by the frequency from $1$ to $12$.
  • The $x$-axis is labeled by the letters $A$, $B$, $C$, and $D$.

  Now we can check the frequency of $A$, $B$, $C$, and $D$ via the length of the bars of each graph. The frequency given in the table must correspond with the frequency given by the bar.

  So we can match as follows, from the left to right:

  • The red bar graph.
  • The green bar graph.
  • The grey bar graph.
  • The blue bar graph.

• Determine the right frequencies.

  Hints

  To count the tally marks easier, note that five tally marks are marked as pictured here:

  First, count the groups of five lines and then the remaining tally marks.

  Here you see $5\times 5+3=28$ lines.

  Solution

  Frequency tables are used to show frequencies:

  • In the first column the animals are listed.
  • In the second column one can write down tally marks for each burp.
  • The last column contains the number of burps. For this we have to count the corresponding tally marks.

  You can see the solution beside.

  • First, count all groups of five tally marks.
  • Next, count the remaining tally marks.
  • The total number is given by adding the number of tally marks altogether.

  Let's have a look at the sheep burps:

  • There are two groups of five tally marks, giving us $5\cdot 2=10$ tally marks.
  • There are three remaining tally marks.
  • Together we have $2\times 5+3=13$ tally marks total.

• Describe the given dot plot.

  Hints

  Think about the frequency of families together with their corresponding number of children.

  Pay attention to the labeling of the axes.

  Solution

  This dot plot shows the frequency of families with one up to five children:

  • There are $3$ families with one child.
  • $8$ families have two children.
  • Most families, namely $12$, have three children.
  • Only $2$ families have four children.
  • $3$ families have five children.

  As many families, namely $4$, have one or five children. The total number of children is

  $3\times 1+8\times 2+12\times 3+2\times 4+3\times 5=78$

  and the total number of families is

  $3+8+12+2+3=28$.