Scale Factor as a Percent

Basics on the topic Scale Factor as a Percent
Scale Factor as a Percent – Definition
In many real-world applications, such as creating scale models or reading maps, understanding the concept of scale factor is crucial. A scale factor is a number which scales, or adjusts, the dimensions of a figure.
Scale Factor as a Percent represents how much a known size has been increased or decreased to reach a new size, expressed as a percentage.
| Scaling Direction | Description | Illustration Request |
|---|---|---|
| Scaling Up | Enlarging an object to a size greater than its original. Commonly used in model building where details need to be visible at a larger scale. | Illustration request: show one smaller triangle with an arrow next to it point to the same triangle but just a larger version |
| Scaling Down | Reducing an object to a size smaller than its original. Used in situations like map making where large areas need to be represented on a smaller, manageable scale. | Illustration request: show one larger triangle with an arrow next to it point to the same triangle but just a smaller version |
Understanding Scale Factor as a Percent – Explanation
Scale factors are often given in various forms, such as ratios or fractions, but converting these to a percent makes comparisons and calculations easier, especially in practical situations like resizing images or blueprints and learning how to create a scale drawing.
To convert a scale factor from a ratio or fraction to a percentage, you simply multiply it by 100.
Scale Factor as a Percent – Step-by-Step Process
Converting a scale factor into a percentage can be useful in understanding how much an object’s size has been changed in models, drawings, or maps. Here’s a step-by-step breakdown of how to convert a scale factor, given as a fraction or ratio, into a percent:
Identify the Scale Factor: First, determine the scale factor used in the scaling. It is usually given as a ratio or fraction (e.g., $1:25$ or $frac{1}{25}$).
Convert the Ratio or Fraction to a Decimal:
If the scale factor is a ratio (like $1:25$), convert it to a fraction $frac{1}{25}$).
To convert a fraction to a decimal, divide the numerator by the denominator $frac{1}{25} = 0.04$.
Convert the Decimal to a Percentage:
- Multiply the decimal by 100 to convert it to a percentage (0.04 \$times$ 100 = 4%).
Interpret the Result:
- A result of 4% means the scaled object is 4% the size of the original.
Illu Request: $1:25$ → $\frac{1}{25}$ → $0.04$ → $4\%$
Here are more examples of scale factors and their conversion to a percentage.
| Scale Factor | Percentage |
|---|---|
| $1:1$ | $100\%$ |
| $1:2$ | $50\%$ |
| $1:5$ | $20\%$ |
| $1:10$ | $10\%$ |
| $1:20$ | $5\%$ |
| $1:50$ | $2\%$ |
| $1:100$ | $1\%$ |
| $1:200$ | $0.5\%$ |
| $2:1$ | $200\%$ |
Scale Factor as a Percent – Example or Practice
Practice some on your own!
Scale Factor as a Percent – Summary
Key Learnings from this Text:
Scale factor simplifies understanding proportions in models and maps.
Converting scale factors to percentages aids in easy and practical application.
The process involves converting the ratio or fraction to a decimal and then to a percentage.
Scale Factor as a Percent – Frequently Asked Questions
Transcript Scale Factor as a Percent
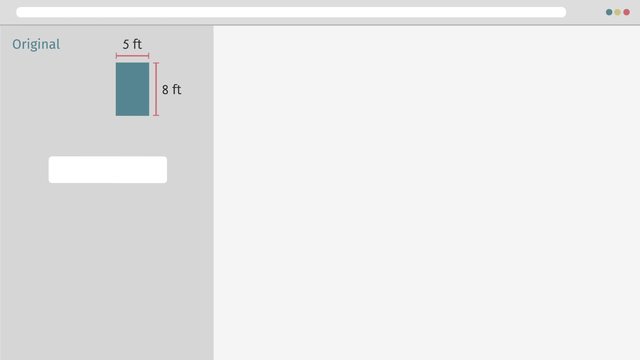
Leelee knows she's got what it takes to become internet famous. So she decides to follow in the footsteps of her favorite celebs and create her own brand. LeeLee Lifestyle: Just Be. To get the word out about her new brand, Leelee plans to make a diverse line of eye-catching posters. But in order to use her digital design software, she's going to also need to use the scale factor as a percent Leelee originally designed her logo to fit on a poster measuring five feet wide and eight feet high. But the launch of an exciting new brand deserves something larger! If she wants to make the dimensions of the poster three hundred percent larger, what will the new dimensions be? You may remember that the scale factor is the same as the constant of proportionality, 'k', between two similar objects. Any length on a scale drawing is equal to the scale factor times the corresponding length on the original drawing. With this formula, we can find the scaled dimensions of Leelee's poster, just by substituting in our known values. Looking at the information we have been provided, what should we use for our scale factor? Leelee wants to increase the dimensions by three hundred percent so we can use 3 as our value for 'k'. Now, how can we use this formula to find our scaled width? We know the original width is five feet, so multiplying that by our scale factor give us the scaled width of fifteen feet. Now, to for the height. The original height of eight feet times our scale factor, 'k' gives us the scaled dimension of twenty four feet. As we expected, our scale factor is greater than one, so the result is an enlargement of the original. "Leelee’s extra-large launch poster is ready to go!" For her next poster, Leelee needs to take her original design, which is tall and skinny, and transform it into something completely different. To do this, she is going to use two DIFFERENT scale factors. For the vertical height, she will use a scale factor of 75 percent. For the horizontal width, she will use a scale factor of 250 percent. A change like this which uses multiple scale factors is called a distortion, because the resulting shape may not look anything like the original. Before we start figuring out the new dimensions, how do you imagine her new poster will look? Well, for the height we have a scale factor less than one, so that is going to create a VERTICAL SHRINK. This means the resulting shape will be shorter than the original. For the width, we have a scale factor of more than one, so that is going to create a HORIZONTAL STRETCH. This means the resulting shape will be wider than the original. Ok, now that we know what kind of distortion we should expect, let's calculate our new dimensions using our formula. We know that our original height is 8 feet and we want to apply a scale factor of 75 percent, or 0.75. That gives us a scaled height of 6 feet. Now that we've done our vertical shrink, let's move on to the horizontal stretch. Once again, plugging in our constant of proportionality and the original width into our formula gives us a scaled width of 12.5 feet. Leelee's new distorted poster would look great on the side of a bus! Or maybe even a really, really big hot dog bun! For her last guerilla marketing effort, Leelee wants to make another distortion. This time, she wants to use a whopping nine hundred and sixty percent for her vertical scale factor. And one fifth for the horizontal scale factor,. Before we figure out the new dimensions, how do you imagine THIS distorted poster will look? Since we are using a scale factor greater than one applied only to the height, that will create a VERTICAL STRETCH. Our other scale factor is less than one and is applied only to the width, that will create a HORIZONTAL SHRINK. Now that we know roughly what kind of shape we can expect, let's calculate our new dimensions. Our vertical stretch uses a scale factor of 960 percent, or 9.6. We multiply that by our original height of 8 feet giving us a scaled height of 76.8 feet. Our horizontal shrink uses a scale factor of one fifth, so that goes in for 'k'. Multiplying that by our original width of 5 feet gives us a new width of one foot. "While Leelee’s posters are being printed, let’s review." The scale factor, 'k', is the constant of proportionality describing the relationship between two related drawings. It can be written as a fraction, decimal, or a percent. If you apply different scale factors to different dimensions, you create a distortion of the original. Distortions applied to the width result in a horizontal stretch...or shink. Distortions applied to the height result in vertical stretch...or shrink. "Leelee's prints are back and she's all set to unveil her brand new marketing campaign!" "Whoa...guess we went a little overboard on the distortion!" Hashtag epic fail!
Scale Factor as a Percent exercise
-
Increasing Dimensions.
HintsAn increase of $600$% means we would multiply by $\frac{600}{100} = 6$. Therefore, the scale factor is $6$.
An increase of $70$% means we would multiply by $\frac{70}{100} = 0.7$. Therefore, the scale factor is $0.7$.
SolutionAn increase of $500$% means we multiply by $\frac{500}{100} = 5$. Scale factor $5$ as shown.
- $200$% $=$ Scale factor $2$
- $75$% $=$ Scale factor $0.75$
- $750$% $=$ Scale factor $7.5$
-
Determine the correct conditions to produce a distortion.
HintsAn object is distorted if the dimensional increase (scale factor) of the vertical is not the same as the one on the horizontal.
For example, a horizontal dimension increase $900$% and vertical dimension increase $500$% would cause a distortion as the scale factors are $9$ and $5$. It could look something like this.
When the scale factor is the same for the vertical and the horizontal the enlargement is not distorted.
For example, a scale factor of $5$ on both vertical and horizontal will not be distorted.
There are $3$ correct answers here.
Solution- Horizontal dimension increase $40$% and vertical dimension increase $400$%. (See this one above)
- Horizontal dimension increase $400$% and vertical dimension increase $500$%.
- Horizontal dimension increase $250$% and vertical dimension increase $350$%.
-
Find the correct dimensions.
HintsHorizontal is across and vertical is up and down.
For a stretch of $700$% we multiply the side by a scale factor of $7$.
For a shrink of $\frac{1}{5}$ we multiply the side by a scale factor of $0.2$.
SolutionThe correct dimensions are horizontally $15$ ft and vertically $1$ ft.
- Horizontal scale factor is $3$, we do $3\times5 = 15$ ft.
- Vertical scale factor is $0.25$, we do $4\times0.25 = 1$ ft.
-
Find the dimensions of a distorted photograph.
HintsHorizontal is across and vertical is up and down.
- For a stretch of $700$% we multiply the side by a scale factor of $7$.
- For a shrink of $35$% we multiply the side by a scale factor of $0.35$.
Multiply each side by the scale factor for the new dimensions.
SolutionThe correct answer is horizontal $6$ ft and vertical $12$ ft.
- A horizontal shrink of scale factor $0.75$ means, $0.75\times8 = 6$ ft.
- A vertical stretch of scale factor $3$ means, $3\times4 = 12$ ft.
-
Use scale factor to increase an item.
HintsAn increase of $500$% is a scale factor of $5$.
Therefore, an increase of $200$% is a scale factor of ?
When we have worked out the scale factor we multiply each side by this scale factor.
As an example, if we had a side length of $2$ft with a scale factor of $6$, we do $2\times6 = 12$ to get the new length.
For example, this rectangle can be increased by $400$%.
- $400$% $=$ a scale factor of $4$
- Multiply the width and height by $4$
- New dimensions are $2\times4 = 8$ft and $3\times4 = 12$ft.
Solution- The correct dimensions are $6$ by $4$
- $200$% $=$ a scale factor of $2$
- Multiply the width and height by $2$
- The new dimensions are $2\times2 = 4$ft and $3\times2 = 6$ft
-
Find the scale factors of the distortions.
HintsTo work out the scale factor, divide the corresponding side on B by the corresponding side on A.
For example here the scale factor is $8\div2 = 4$. Therefore, the stretch horizontally is $4 \times 100 = 400$%.
If the corresponding side on B is smaller then it is a shrink.
For example, here the scale factor is $\frac{2}{10} = \frac{1}{5}$. To find the percentage we do $100 \times \frac{1}{5} = 20$%.
SolutionGreen rectangles
- Horizontal stretch is $4\div2 = 2 = 200$%.
- Vertical shrink is $6\div8 = \frac{3}{4} = 75$%.
- Horizontal shrink is $2\div4 = \frac{1}{2} = 50$%.
- Vertical stretch is $9\div3 = 3 = 300$%.
- Horizontal stretch is $12\div3 = 4 = 400$%.
- Vertical shrink is $4\div5 = \frac{4}{5} = 80$%.
- Horizontal shrink is $3\div5 = \frac{3}{5} = 60$%.
- Vertical stretch is $10\div4 = 2.5 = 250$%.










#epicfail
hahahahaahhahahhahahahaa