Magnitude
- Understanding Magnitude through Powers of Ten – Introduction
- Understanding Magnitude – Definition
- Magnitude and Powers of Ten – Example
- Magnitude and Powers of Ten – Guided Practice
- Magnitude and Powers of Ten – Exercises
- Understanding Magnitude through Powers of Ten – Summary
- Understanding Magnitude through Powers of Ten – Frequently Asked Questions

Basics on the topic Magnitude
Understanding Magnitude through Powers of Ten – Introduction
When we look at the world around us, we see a vast range of sizes, from the microscopic to the astronomical. Grasping the sheer scale of different objects can be challenging without a way to measure and compare them. This is where the concept of magnitude and the use of powers of ten come in handy, especially for 8th-grade students learning about exponential notation and scientific notation.
Understanding Magnitude – Definition
Magnitude refers to the size or extent of something, often measured in terms of its power or scale. In mathematics, we frequently use powers of 10 to represent and compare the magnitude of very large or very small quantities. A power of ten is 10 raised to an exponent, which indicates how many times to multiply 10 by itself.
To make sense of magnitude, let's look at some rules and steps:
| Concept | Description |
|---|---|
| Powers of Ten | Written as $10^{n}$, where $n$ is the exponent. Large numbers have positive $n$, small numbers have negative $n$. |
| Scientific Notation | A method to express numbers as a product of a number between 1 and 10 and a power of ten, e.g., 320 as $3.2 \times 10^{2}$. |
| Comparing Magnitudes | To compare two numbers in scientific notation, check their exponents; the larger exponent indicates a greater magnitude. |
Magnitude and Powers of Ten – Example
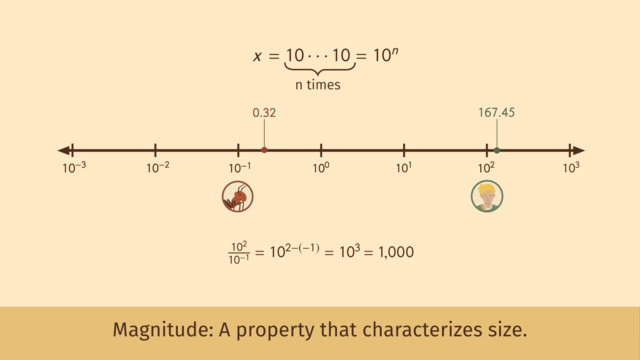
Let's take David's curiosity about the size difference between himself and Hans the ant as an example. David is 167.45 centimeters tall, which can be approximated to $1.67 \times 10^{2}$ centimeters in scientific notation. The ant, being 0.32 centimeters long, is approximately $3.2 \times 10^{-1}$ centimeters.
To find out how many times larger David is than Hans, we compare the powers of ten:
$ \frac{1.67 \times 10^{2}}{3.2 \times 10^{-1}} $
Here, we do not need the exact numbers but instead focus on the exponents:
$10^{2} \div 10^{-1} = 10^{2 - (-1)} = 10^{3} $
So, David is about $10^{3}$, or 1,000 times larger than Hans.
Magnitude and Powers of Ten – Guided Practice
Imagine you're comparing the height of a basketball player, who is 2 meters tall, to the length of a basketball, which is about 24 centimeters in diameter.
Magnitude and Powers of Ten – Exercises
Now, let's apply what we've learned to a new scenario.
Understanding Magnitude through Powers of Ten – Summary
Key Learnings from this Text:
- Powers of ten help us estimate and compare the size of various entities.
- Scientific notation is a valuable tool for expressing very large or very small numbers.
- By comparing exponents, we can easily determine how many times larger or smaller one quantity is than another.
- Understanding the magnitude and powers of ten is essential for real-world applications and scientific understanding.
Explore more about powers of ten and their applications with interactive practice problems, engaging videos, and printable worksheets on our platform to enhance your learning experience.
Understanding Magnitude through Powers of Ten – Frequently Asked Questions
Transcript Magnitude
David is a young naturalist, curious about all things great and small. He marvels at how small the ant is compared to him. David feels a kinship with this little creature, and names the ant Hans. David is a lot bigger than Hans. But in order to truly compare their sizes. David will need to understand the concept of magnitude. Hans measures point three two centimeters. From Hans's perspective, David is a giant! David measures 167.45 cm. Subtracting isn't so instructive. One hundred and sixty seven point four five minus zero point three two is 167.13 cm, but that doesn't tell us much. A better question is, about how many times bigger is David compared to Hans? Instead of SUBTRACTING, we can compare the magnitudes of David and Hans. Magnitude is a property of a number that characterizes its size. How do we find the magnitude of Hans's and David's height? To get a rough approximation, we find a nearby power of 10. Remember, a power of 10 is any number which can be written as 10 multiplied by itself a certain number of times. So 1, or 10 to the 0, 10 to the 1, 10 to the -1, 10 to the 2, 10 to the negative 2, and so on are all powers of 10. Hans is point three two cm long. What is the closest power of 10 to point three two? It is 10 to the negative 1. The negative 1 exponent is an expression of Hans's magnitude. By itself, 10 to the negative one still doesn't tell us much. The interesting question for a curious naturalist is, how does David's magnitude compare to Hans's? Let's approximate David's magnitude. David is 167.45 cm tall. What is the power of 10 closest to 167.45? First let's find the closest power of 10 which is bigger than 167.45. 168 is the very next integer. 999 still has 3 digits so then, 1000 is the next power of 10! Or ten to the 3rd. We can also look to see if there is a power of 10 smaller than David's height which is even closer than 10 to the 3. The first power of 10 we find is 10 to the 2. As 10 to the 2 is closer to David's height than 10 to the 3, we will take 10 to the 2 as David's magnitude. Now let's compare the magnitude of David and Hans. We want to know how many powers of 10 bigger David is than Hans. Dividing David's magnitude by Hans's will give us the difference. David is roughly 10 to the 3, or 1000 times bigger than Hans. In general, how do we approximate and compare magnitudes? A number line can help us visualize the process. Suppose we have the number 2010 point four. First, we observe that there are integers on either side of this value. 2,010 and 2,011. Then, we find the closest power of 10 above and the closest power of 10 below these integers. Counting up from 2011 takes us to 9,999, and the next number is 10,000, or 10 to the 4th. 10,000 has four zeros, so our power of 10 is 10 to the 4th. Counting down from 2,010 takes us to 1,000, or 10 to the 3rd. In general, for ANY number 'M', we can find an integer 'N' below it and an integer 'N+1' above it. If 'N+1' has 'k' digits, 10 to the 'k' will be the nearest power of 10 bigger than 'M' and 10 to the 'k-1' will be the nearest power of 10 smaller than 'M'. A number line also helps us visualize COMPARING the magnitude of numbers. We know that David is roughly 10 to the 3, or 100 times as big as Hans the ant. But David is a curious naturalist and wonders how big the earth is compared to himself. Let's use powers of 10 to compare the magnitudes of David and the earth. Remember, David is 167.45 cm tall. The earth is a stunning one trillion two hundred seventy-four billion two hundred million cm in diameter! Let's find the magnitude of the diameter of the earth and compare it to David's magnitude. What's the closest power of 10 to David's height? As we found before, it is 10 to the two. What's the closest power of 10 to the diameter of the earth? Ten to the twelve. Dividing the earth's magnitude by David's magnitude we see that the earth is roughly 10 to the 10, or 10 billion times as big as David. David is 1,000 times bigger than Hans the ant, but the earth is 10 billion times bigger than David. Woah. Let's review. Magnitude is a property of a number that characterizes its size. We can approximate a number by finding the nearest powers of 10 bigger or smaller than the number. We can compare magnitudes by dividing the bigger power of 10 by the smaller one. The result tells us how many times as big the bigger number is compared to the smaller. Magnitude helps David comprehend how much bigger he is than Hans the ant. It also helps David comprehend how much bigger the earth is than him. There is no limit to the magnitudes we can compare in the universe.
Magnitude exercise
-
Understanding the powers of ten.
HintsA power of $10$ is as many number $10$'s as indicated by the exponent, multiplied together. For example, $10^2= 10\times10$.
- $10^2 = 10\times10 = 100$
- $10^3 = 10\times10\times10 = 1,000$
- $10^4 = 10\times10\times10\times10 = 10,000$ etc.
- $10^{-1} = 1\div10 = 0.1$
- $10^{-2} = 1\div100 = 0.01$
- $10^{-3} = 1\div1000 = 0.001$ etc.
Solution- $10^2 = 10\times10 = 100$
- $10^3 = 10\times10\times10 = 1,000$
- $10^5 = 10\times10\times10\times10\times10 = 100,000$
- $10^{-2} = 1\div100 = \frac{1}{100} = 0.01$
-
Estimate the nearest power of 10.
HintsFirst work out the values of the powers of $10$
When you have worked out the values of the powers of $10$, decide where the value sits on this line.
Which power of $10$ is nearest?
SolutionThe correct answer is $10^2$.
$10^2 = 100$. This is the closest power of $10$ to $238$.
$238$ falls between $100$ and $1,000$ but is closer to $100$.
-
Difference in magnitude
HintsTo work out the difference in magnitude we divide the powers of $10$.
For example,
When we subtract a negative we actually add it.
For example $8 - (-5) = 8 + 5 = 13$
Solution- Magnitudes $10^4$ and $10^3 = 10^4\div10^3 = 10^1 = 10$
- Magnitudes $10^5$ and $10^3 = 10^5\div10^3 = 10^2 = 100$
- Magnitudes $10^5$ and $10^0 = 10^5\div10^0 = 10^5 = 100,000$
- Magnitudes $10^3$ and $10^{-1} = 10^3\div10^{-1} = 10^4 = 10,000$
-
Find the difference in magnitudes
HintsFirst, work out the magnitude of Dan's height and the magnitude of the height of the building by deciding which power of $10$ they are nearest to.
When you have the magnitude, divide the magnitude of the building by the magnitude of Dan's height.
For example, $10^5\div10^3 = 10^2 = 100$ times taller.
SolutionThe correct answer is $10^2$.
Dan's magnitude is nearest to $10^1$.
The magnitude of the building is nearest to $10^3$.
Divide them to work out the difference.
$10^3\div10^1 = 10^2 = 100$ times taller.
-
Estimate the power of $10$ nearest to $3,500$.
HintsMagnitude is a property that characterizes size, so we are looking for the nearest power of $10$ to our number.
Work out the value of each power of $10$ around the number.
Decide where the value sits on the line and choose the power of $10$ which is nearest. We can see $3,500$ lies between $1,000$ and $10,000$, but which one is it nearer to?
The number line here shows the position of $3,500$. Which power of $10$ is nearest?
SolutionThe magnitude is $10^3$.
$10^3 = 1,000$ and $10^4 = 10,000$. $3,500$ falls between $1,000$ and $10,000$ and is nearer to $1,000$. Therefore, the magnitude is $10^3$.
-
Find the difference in magnitude.
HintsFirst, find the magnitude of the distance around the earth and the magnitude of the distance to the beach by deciding which power of $10$ they are closest to.
When you have the magnitude, divide the magnitude of the distance around the earth by the magnitude of the distance from home to the beach.
For example, $10^6\div10^2 = 10^4 = 10,000$ times longer.
Solution$10^3 = 1,000$ times longer
- The magnitude of the distance around the earth is nearest to $10^4$.
- The magnitude of the distance from home to the beach is $10^1$.
- Divide them to find the difference.
$10^4\div10^1 = 10^3 = 1,000$ times further around the earth than from home to the beach.