Choosing Appropriate Units with Scientific Notation
- Units with Scientific Notation – Introduction
- Scientific Notation – Definition
- Writing Numbers in Scientific Notation – Step-by-Step Process
- Scientific Notation – Practice
- Choosing Appropriate Units in Scientific Notation
- Converting Scientific Notation to Standard Form – Application
- Choosing Appropriate Units with Scientific Notation – Summary
- Introduction to Scientific Notation – Frequently Asked Questions

Basics on the topic Choosing Appropriate Units with Scientific Notation
Units with Scientific Notation – Introduction
Scientific notation is a powerful tool for expressing and handling extremely large or incredibly small numbers. It simplifies calculations, comparison, and representation of numbers that would otherwise be unwieldy to work with.
Scientific notation is thus an essential component of the scientific community’s toolkit, enabling clear communication and efficient computation across disciplines such as physics, chemistry, astronomy, and beyond.
Scientific Notation – Definition
In scientific notation, a number is written as the product of two factors: a coefficient that is greater than or equal to 1 and less than 10, and the number 10 raised to an exponent. The exponent reflects how many places the decimal point has moved.
For example, the number 5,600,000 can be written as $5.6 \times 10^{6}$ in scientific notation.
Writing Numbers in Scientific Notation – Step-by-Step Process
Here are some basic rules to follow:
- The coefficient must be a number between 1 and 10.
- The exponent indicates how many places the decimal point has moved to the right for positive exponents, or to the left for negative exponents.
Scientific Notation – Practice
Express the distance between the Earth and the Sun, approximately 149,600,000 kilometers, in scientific notation.
- Identify the coefficient: Move the decimal point to create a number between 1 and 10. Here, we move it 8 places left to get 1.496.
- Determine the exponent: Since we've moved the decimal point 8 places, the exponent is 8.
- Combine the coefficient and exponent: Write the number in the form $c \times 10^{n}$, where c is the coefficient and n is the exponent.
So, the distance is written as $1.496 \times 10^{8}$ kilometers in scientific notation.
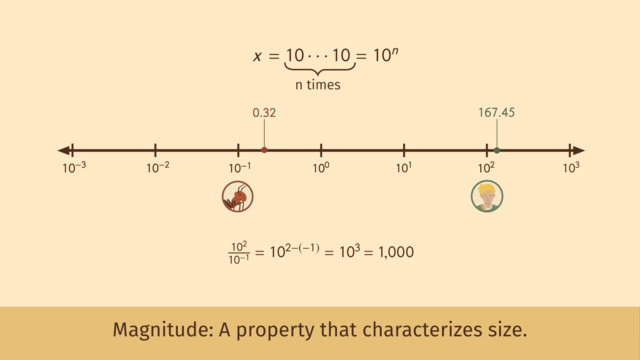
Choosing Appropriate Units in Scientific Notation
When working with scientific notation, it's crucial to select units that make the numbers manageable and meaningful within the context. The choice of units can significantly affect the readability and practicality of the results. Here are key considerations:
- Relevance to the Field: Choose units that are standard in the field of study or industry to facilitate understanding and comparison.
- Magnitude of Measurement: Opt for units that bring the coefficient within the 1-10 range. For instance, using kilometers instead of meters for astronomical distances can make the numbers easier to work with.
- Consistency: Maintain consistent units across calculations to ensure accuracy and prevent confusion, especially when multiplying or dividing quantities in scientific notation.
Example If measuring the thickness of a human hair, typically around 0.1 millimeters, it's practical to express this measurement in micrometers in scientific notation:
- Standard measurement: 0.1 mm
- Convert to micrometers: 100 micrometers
- Scientific notation: $1 \times 10^{2}$ micrometers
By choosing micrometers instead of millimeters, the scientific notation stays simple and clear, with a coefficient within the optimal range.
Converting Scientific Notation to Standard Form – Application
Choosing Appropriate Units with Scientific Notation – Summary
Key Learnings from this Text:
- Scientific notation simplifies the representation of extremely large or small numbers, making them easier to work with and understand.
- It consists of a coefficient and a power of 10, facilitating easier calculations and comprehension.
- Multiplying and dividing with scientific notation involves working with exponents, and simplifying complex calculations.
- Converting between scientific notation and standard form is crucial for proper understanding and communication.
- Choosing appropriate units in scientific notation is vital to ensure the data is manageable and meaningful, enhancing clarity and effectiveness in communication.
To further develop your knowledge and skills, explore more content on our platform, including interactive practice problems, videos, and worksheets focused on scientific notation and other mathematical concepts.
Introduction to Scientific Notation – Frequently Asked Questions
Transcript Choosing Appropriate Units with Scientific Notation
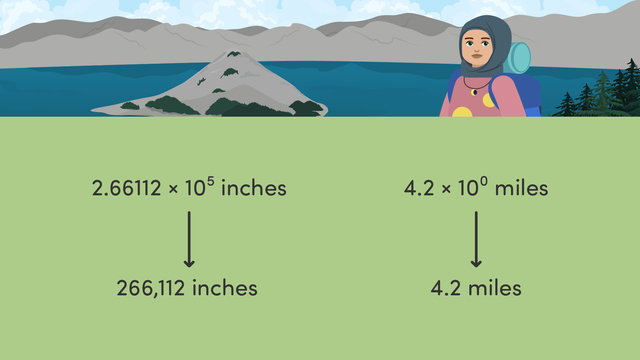
"Wow, Kai, that was some hike up Mount Crumble!" "You weren't joking when you said we would be getting in a workout, but I had no idea what a hike like this would entail!" Kai and Penny will be 'choosing appropriate units with scientific notation' to see what they have accomplished on their hike. Remember, scientific notation is a way to express very large or very small numbers using powers of ten. We can use our knowledge of powers of ten to help us compare numbers in scientific notation. However, it is also important to remember to choose appropriate units when comparing and interpreting any numbers. Keeping this in mind, let's look at Kai and Penny's post-hike stats that have been recorded on each of their smartwatches. According to Kai's stats, the distance that the pair hiked is seen here. When Penny looks at her watch, the distance hiked is displayed as this. If we look at these numbers in standard form, Kai's watch will report two hundred sixty-six thousand, one hundred twelve inches hiked. And Penny's would be four and two-tenths miles. They hiked the same exact distance, so these numbers are equivalent, but using different units. In this case, Penny's watch stats give a more APPROPRIATE unit of measure for the hike. With this kind of distance, using miles is easier to understand. Kai and Penny next scroll to the stat on TIME to see how long their hike ultimately was. According to Kai's smartwatch stats, the hike lasted this many days. Penny's watch recorded the hike to be three and nine-tenths times ten to the second power minutes long. These numbers in standard form are written as. If we had to choose between these two measurements, the minutes would be MORE appropriate of the two because, again it is easier to comprehend. However, there would be an even MORE appropriate unit here to measure the hiking time. Pause the video here to think if you can come up with a better unit of measurement. Hours! Three hundred and ninety minutes can be divided by sixty, which equals six and a half hours, making it a more appropriate unit for measuring time in this context. The last stat that Kai and Penny will look at is the elevation of Mount Crumble. Kai's stats report that the elevation they gained was one and seven hundred four thousandths multiplied by ten to the power of three feet. Penny's report is in inches and is two and four hundred forty-eight ten thousandths times ten to the fourth power. Pause here, and determine which hiker's measurements would be appropriate to measure the elevation of a mountain. Kai's smartwatch measurement of one thousand seven hundred four feet is more appropriate when measuring the elevation of a mountain. Let's summarize what we have learned. Scientific notation is a way to express very large or very small numbers using powers of ten. Data given to us in this form can be interpreted and compared to help us choose the most appropriate unit of measurement. "The best part about hiking Mount Crumble is the amazing photos I got for some sweet social media posts!"
Choosing Appropriate Units with Scientific Notation exercise
-
What is scientific notation?
HintsOur knowledge of powers of ten helps us to compare numbers in scientific notation by understanding that multiplying by 10 raises the number by one power, and dividing by 10 lowers the number by one power.
For instance, comparing $4.5 \times 10^6$ and $7.2 \times 10^5$, we know that $4.5 \times 10^6$ is larger because it has a higher power of ten ($6$ compared to $5$).
SolutionScientific notation is a way of writing numbers that are very large or very small using powers of ten.
For example, $6.02 \times 10^{23}$ represents a very large number, and $3.2 \times 10^{-5}$ represents a very small number.
-
Which unit of measurement is more appropriate for expressing the length?
HintsReflect on the standard units used for measuring distances and their relevance in everyday contexts.
Which unit is commonly used for larger distances, especially when discussing geographic features like rivers?
When dealing with large distances, using a consistent unit like miles allows for easier comparisons and calculations.
It avoids the need for extensive conversions and simplifies data analysis.
SolutionSarah's measurement is $2.02752 \times 10^{5}$ inches.
Jack's measurement is $3.2$ miles.
In this case, measuring in miles would be more appropriate for determining the length of the river.
-
Compare these measurements and decide which one is easier to work with in calculations.
HintsThink about the scale of the measurement.
Consider whether the mass being measured is relatively large or small, and choose a unit of mass that makes sense in that context.
Reflect on the precision required for the measurement.
Consider whether using grams alone is sufficient, or if you need to consider smaller units like milligrams for more accurate measurements.
Solution45 grams.
If you need a more precise measurement or are dealing with smaller masses, grams would be a better option.
For example, in scientific experiments or when measuring ingredients in cooking, grams are commonly used.
-
Determine which unit of measurement is more practical for describing the pool's volume.
HintsConsider the scale of the measurement.
Think about which unit (cubic inches or cubic feet) would result in a more manageable and easy-to-understand number for describing the size of a swimming pool.
Reflect on which unit (cubic inches or cubic feet) is commonly used for larger volumes like swimming pools in everyday conversations or real-world applications.
SolutionUsing cubic feet is more practical for describing the pool's volume because it results in a smaller, more manageable number without the need for scientific notation.
Additionally, cubic feet is a commonly used unit for measuring larger volumes like swimming pools, making it more familiar and understandable in everyday contexts.
-
Convert a number in scientific notation to standard form.
HintsConsider the power of $10$.
The exponent $2$ indicates how many places to move the decimal point.
Recall that $10^2$ = $100$.
Solution$5 \times 10^2$ in standard form is $500$.
-
Convert numbers in scientific notation to standard form.
HintsMeters are a standard unit of length used in scientific contexts, especially for large distances like the distance from Earth to the Moon.
Using meters provides a more appropriate and universally understood.
Using grams provides a more precise and detailed measurement for a scientific experiment analysis.
Using cubic feet instead of cubic inches would be more practical for measuring the volume of a swimming pool.
Since swimming pools are typically large structures, using cubic feet provides a more manageable and understandable measurement.
Additionally, working with cubic feet allows for easier visualization of the pool's size and simplifies calculations.
SolutionThe distance from Earth to the Moon - $3.84\times 10^{5}$ meters
The mass of a tennis ball - $7.2\times 10^{5}$ grams
The volume of a swimming pool - $9.2\times 10^{4}$ cubic feet