Fractions with the Same Denominator

Basics on the topic Fractions with the Same Denominator
Comparing Fractions with Like Denominators
Before we compare fractions with the same denominators, we must think about what a denominator means. Denominators show how many equal parts a whole is divided into. Fractions with the same denominators are called like fractions as long as the whole is identical.
The fraction with the greater numerator will always be larger when comparing like fractions from the same whole. This is because each part is the same size, and the greater numerator is telling us we have more of the equal parts. Fraction models can help us see if like fractions are greater than, less than, or equal to one another. How do you compare fractions with like denominators? Read on below to learn how!
Comparing Fractions with the Same Denominator – Steps
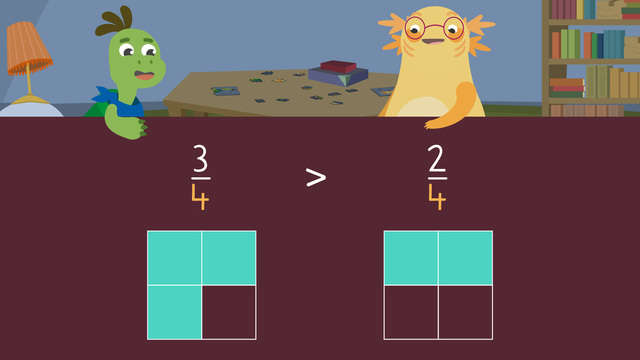
Let's practice comparing the like fractions three fourths and two fourths. They are like fractions because both have the same denominator and come from the same whole. First, draw and shade a fraction model to represent three fourths.
Then, draw and shade another identical fraction model to represent two fourths.
Finally, compare the shaded values of both models.
Three fourths has more parts shaded than two fourths. So three fourths is greater than two fourths. Remember, the like fraction with the greater numerator is larger.
That is how to compare fractions with the same denominator but different numerators.
Comparing Fractions with the Same Denominator – Summary
These are the steps for comparing fractions with the same denominator:
| Step # | What to do |
|---|---|
| 1 | Draw and shade a fraction model to represent the first fraction. |
| 2 | Draw and shade another identical fraction model to represent the second fraction. |
| 3 | Compare the shaded values of both models. |
| 4 | The fraction with more shaded parts is greater! |
Have you practiced yet? On this website, you can also compare fractions with the same denominator with worksheets and exercises.
Transcript Fractions with the Same Denominator
Axel and Tank are working on puzzles of identical size. Axel has ten of the twelve pieces in place. Tank has nine of the twelve pieces in place. They want to compare who's finished more, so we'll need to teach them about "Fractions with the Same Denominator". Denominators tell us how many equal parts a whole is divided into. Fractions with the same denominators are called “like fractions” as long as the whole is identical. The fraction with the greater numerator will always be larger when comparing like fractions from the same whole. This is because each part is the same size, and the greater numerator is telling us we have more of the equal parts. Fraction models can help us see if like fractions are greater than, less than, or equal to one another. Let's compare the like fractions three fourths and two fourths. They are like fractions because both have the same denominator and come from the same whole. First, draw and shade a fraction model to represent three fourths. Then, draw and shade another identical fraction model to represent two fourths. Finally, compare the shaded values of both models. Three fourths has more parts shaded than two fourths. So three fourths is greater than two fourths. Remember, the like fraction with the greater numerator is larger. Now let's take a look at Axel and Tank's puzzle progress. We have eight twelfths and ten twelfths. First, draw and shade a fraction model to represent eight twelfths. Then, draw and shade another identical fraction model to represent ten twelfths. Finally, compare the shaded values of both models. Eight twelfths has fewer parts shaded than ten twelfths. So, eight twelfths is less than ten twelfths. The like fraction with the smaller numerator is smaller. Let's try this again using the progress from Axel and Tank's last puzzles. Tank has eleven fifteenths finished and Axel has nine fifteenths finished. Who has more of their puzzle done? Tank has more of his puzzle done because the numerator of his like fraction is greater than Axel's. How can we check our answer? We can use fraction models! First, draw and shade a fraction model to represent eleven fifteenths. Then, draw and shade another identical fraction model to represent nine fifteenths. Finally, compare the shaded values of both models. Eleven fifteenths has more parts shaded than nine fifteenths, so eleven fifteenths is greater than nine fifteenths. Tank has done more of his puzzle than Axel! While Axel and Tank finish their puzzles, let's review! Fractions with the same denominator are called “like fractions” as long as the whole is identical. When working with like fractions from the same whole, the fraction with the larger numerator will always be larger. We can check our work by setting up identical fraction models. First, draw and shade a fraction model to represent the first fraction. Then, draw and shade another identical fraction model to represent the second fraction. Finally, compare the shaded values of both models. The fraction with more shaded parts is greater! Axel and Tank have both finished their last puzzle now! But why do they look puzzled? "Tank, do you think some of our pieces got shuffled?"
Fractions with the Same Denominator exercise
-
When comparing like fractions with identical wholes, the fraction with the greater numerator will always be _______.
HintsRemember like fractions have the same denominator.
Which fraction has more equal parts shaded in here?
Remember, each part is the same size and the greater numerator is telling us we have more of the equal parts.
SolutionWhen comparing like fractions with identical wholes, the fraction with the greater numerator will always be larger
You can see this in the image above. Each part is the same size and the greater numerator is telling us we have more of the equal parts.
-
Which expressions are true?
HintsRemember when comparing like fractions (with the same denominator) that also have the same whole, the larger numerator will always be the larger fraction.
< means less than and > means greater than.
When looking at the fraction models, which fraction has more equal parts shaded in? That will be the larger fraction.
SolutionShown are the correct expressions. Remember, when comparing like fractions with the same whole, the larger numerator will also be the larger fraction.
The first expression is incorrect because $\frac{1}{3}$ is < $\frac{2}{3}$
The second expression is correct because $\frac{3}{6}$ is < $\frac{4}{6}$
The third expression is incorrect because $\frac{7}{8}$ is > $\frac{6}{8}$
The fourth expression is correct because $\frac{5}{6}$ is > $\frac{4}{6}$
-
Comparing fractions.
HintsRemember when comparing like fractions (with the same denominator) that also have the same whole, the larger numerator will always be the larger fraction.
< means less than and > means greater than.
When looking at the fraction models, which fraction has more equal parts shaded in? That will be the larger fraction.
SolutionRemember, when comparing like fractions with the same whole, the larger numerator will also be the larger fraction.
$\frac{3}{3}$ > $\frac{2}{3}$
$\frac{1}{6}$ < $\frac{2}{6}$
$\frac{2}{8}$ < $\frac{3}{8}$
$\frac{6}{8}$ > $\frac{5}{8}$
-
Greater than or less than?
HintsRemember when comparing like fractions that also have the same whole, the larger numerator will always be the larger fraction.
< means less than and > means greater than.
Solution$\frac{5}{6}$ < $\frac{6}{6}$
$\frac{4}{6}$ < $\frac{5}{6}$
$\frac{2}{8}$ > $\frac{1}{8}$
$\frac{4}{8}$ > $\frac{3}{8}$
-
What are like fractions?
HintsLike fractions need to have the same whole.
When comparing like fractions we compare the numerators.
Here are 2 like fractions.
SolutionLike fractions are fractions that have the same whole and the same denominator.
Shown is an example of like fractions.
-
Who ate more pizza?
Hints< means less than and > means greater than.
The second set of fractions don't have the same size whole, so you need to look at the size of the pieces.
Make sure you're looking at how many pieces are shaded in.
SolutionFor the first set, they got the same size pizza so, $\frac{2}{5}$ < $\frac{3}{5}$
For the second set, they didn't get the same size pizza so, $\frac{1}{4}$ > $\frac{2}{4}$ because the size of the pieces were larger.
For the third set, they got the same size pizza so, $\frac{4}{8}$ = $\frac{4}{8}$




















I love this program it is so fun