Area of Right Triangles
- Area of Right Triangles – Formula
- Finding Area of Right Angles
- Area of Right Triangles – Step-by-Step Instructions
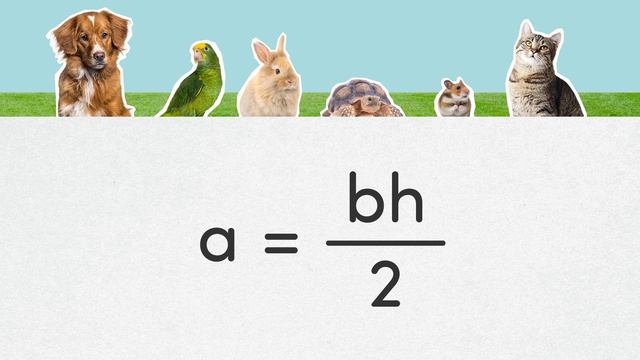

Basics on the topic Area of Right Triangles
Area of Right Triangles – Formula
The area of a right triangle is an essential concept in geometry. Thinking back to things you already have learned, finding the area of a rectangle, will prove to be helpful with this topic! This concept not only helps in understanding basic geometric shapes but also lays the foundation for more advanced topics in mathematics.
The area of a right triangle is the amount of space inside the triangle. It is calculated by taking half of the product of the triangle's base and height.
Before learning how to calculate the area of right triangles, it is important to be able to classify different types of triangles successfully. Complete a quick Triangle Review by watching a video. You can also recap the topic of Classifying Triangles by Angles by watching a video.
Finding Area of Right Angles
To understand the area of right triangles, it's important to know what a right triangle is. A right triangle has one angle measuring 90 degrees. The sides forming the right angle are called the legs, and the side opposite the right angle is the hypotenuse.
| Key Concept | Explanation |
|---|---|
| Right Triangle | A triangle with one 90-degree angle. |
| Base and Height | The two sides forming the right angle. |
| Hypotenuse | The longest side, opposite the right angle. |
Area of Right Triangles – Step-by-Step Instructions
Let's explore a practical example to deepen our understanding of calculating the area of right triangles. We'll use a step-by-step approach to ensure clarity.
Example Problem
Calculate the area of a right triangle with a base of 8 in. and a height of 5 in.
Step-by-Step Solution
- Identify the Base and Height
Base = 8 in. Height = 5 in.
- Apply the Area Formula
The formula for the area of a right triangle is Area=$\frac{1}{2}$ × base × height.
- Substitute the Values into the Formula
Area = $\frac{1}{2}$× 8 × 5
- Perform the Multiplication
First, multiply the base and height: 8 × 5 = 40
8 × 5 = 40 $\text{in}^2$
Then, multiply by $\frac{1}{2}$: 40 × $\frac{1}{2}$ = 20 $\text{in}^2$
- Write Down the Final Answer (including your units)
The area of the triangle is 20 $\text{in}^2$.
Area of Right Triangles – Guided Practice
Let’s work through the following question together.
Calculate the area of a right triangle with a base of 6 cm and a height of 4 cm.
Area of Right Triangles – Exercises
Area of Right Triangles – Summary
Key Points:
The area of a right triangle is calculated as half the product of its base and height.
The formula for the area of a right triangle is Area=$\frac{1}{2}$ × base × height.
*Follow the steps to find the area of any right triangle: identify the base and the height, apply the area formula, substitute the values in the formula, perform the multiplication and write down the answer. Always remember to add square units with your answer. For example: $\text{cm}^2 $.
- Understanding the properties of right triangles is crucial for solving area problems.
You can now explore how to calculate area of obtuse triangles as well as area of acute triangles.
Explore more interactive and engaging geometry lessons on our website, complete with practice problems, videos, and worksheets!
Area of Right Triangles – Frequently Asked Questions
Transcript Area of Right Triangles
Pet parkour day is here! Pets are split up onto two obstacle courses according to size. Large pets use the bigger field, and tiny pets use the smaller field. To see which of the two fields each pet will use, we need to calculate the size of the fields by finding the area of right triangles. A right triangle is a triangle that has a right, or ninety degree, angle. Area is the portion of space that is taken up inside the boundary of a two dimensional shape. The side opposite to the right angle is called the hypotenuse. The other two sides are called the legs. This leg is the base, and this leg is the height. We use the base and height to find the area of right triangles, by using the formula area equals base multiplied by height divided by two. When you see two or more variables written in this way, it means you multiply them together. The formula for finding the area of right triangles can also be written as area equals half multiplied by base multiplied by height, but today, we will be using this formula. The formula is similar to finding the area of a rectangle, which is base multiplied by height, with an added step of dividing it by two, since the area of a right triangle is half the size of a composed rectangle. Let's solve the area of the first field now. First, write the formula we are using. This leg is the base, so replace 'b' with ten. This leg is the height, so replace 'h' with eight, inserting the multiplication symbol. Ten times eight equals eighty. The final step is to solve eighty divided by two, which is forty, adding the unit of measurement, yards. The area of the first field is forty yards squared. Area is always expressed as squared because it is the number of unit squares required to completely cover it. Now the area of the first field has been solved, let's look at the second field. This time, try it on your own before we review. Pause the video to work on the problem, and press play when you are ready to begin. First, write out the formula we are using, area equals base times height divided by two. This leg is the base, so replace 'b' with twelve. This leg is the height, so replace 'h' with twelve. Twelve multiplied by twelve is one hundred forty-four. Divide one hundred forty-four by two, which is seventy-two, and add the unit of measurement. The area of the second field is seventy-two yards squared. Well, it looks like the smaller pets will be on course 'a', and the bigger pets will be on course 'b'! While Pet Parkour gets under way, let's summarize. The formula area equals base multiplied by height divided by two helps to find the area of right triangles. Replace 'b' with the base measurement, and replace 'h' with the height measurement. Multiply these two values together, then divide the product by two to find the area. Don't forget to note the unit of measurement. Well, we may have sorted the pets onto the correct courses, but it sure looks like they all need a lot more training for Pet Parkour!
Area of Right Triangles exercise
-
Label the parts of the triangle.
HintsThe side opposite to the right angle, is the hypotenuse.
Use the letters to help determine where the height and base are on the triangle.
SolutionThe hypotenuse is the side opposite the right angle.
The base is the side that lays flat.
The height is the side that stands tall.
-
What is the formula used to find the area of a right triangle?
HintsTo find the area of a rectangle, you multiply the base by the height.
A triangle is half of a rectangle.
To find the area of a triangle, you multiply the base by the height and then divide this by 2.
When two letters are right next to each other (e.g. $bh$) these are multiplied together.
SolutionTo find the area of a triangle, you multiply the base by the height and then divide it by 2.
-
Calculate the area of the triangle by completing the formula.
HintsUse the formula $a =\frac{bh}{2}$. Fill in the base and height using the diagram.
Once you have multiplied the base by the height, what do you need to divide this by?
SolutionUsing the formula $a =\frac{bh}{2}$, we can find the area of this triangle.
- First, multiply the base by the height. 8 x 4 = 32
- Then, divide this amount by 2. 32 ÷ 2 = 16
- The area of the triangle is 16 yds$^2$.
-
Find the area of the triangle.
HintsUse this formula to find the area of the triangles.
To find the area of this triangle, multiply 8 by 10. Then, divide by 2.
SolutionUsing the formula $a =\frac{bh}{2}$, we can find the area of the above triangles.
- First, substitute the b and h in the formula with the base and height of the triangle.
- Next, multiply these two numbers together.
- Finally, divide this amount by 2.
- The area of the four triangles can be worked out as shown below:
3 x 4 = 12.
- 12 ÷ 2 = 6 yds$^{2}$.
- 16 ÷ 2 = 8 yds$^{2}$.
- 80 ÷ 2 = 40 yds$^{2}$.
- 60 ÷ 2 = 30 yds$^{2}$.
-
Calculate the area of the right triangle.
HintsTo find the area of a triangle, use this formula.
The height is 4 and the base is 10.
First, multiply the base by the height.
What is the next step?
SolutionTo find the area of the triangle, use the formula: $a =\frac{bh}{2}$.
- First, multiply the base by the height. 10 x 4 = 40.
- Next, divide this by 2. 40 ÷ 2 = 20.
- The area of the triangle is 20 yds$^2$.
-
Calculate the area for each triangle.
HintsTo calculate the area of a triangle, multiply the base and height. Then, divide by 2.
To find the area of this triangle, use the measurements for the base (12) and height (12) and put into the formula a = b x h divided by 2.
- 12 x 12 = 144.
- 144 ÷ 2 = 72.
- The area of the triangle is 72 yds squared.
SolutionTo calculate the area of a triangle, use the formula:
a = b x h ÷ 2.
To find the area of the first triangle in the image, use the measurements for the base (8) and height (5) and put into the formula a = b x h ÷ 2.
- 8 x 5 = 40.
- 40 ÷ 2 = 20.
- The area of the triangle is 20 yds squared.














