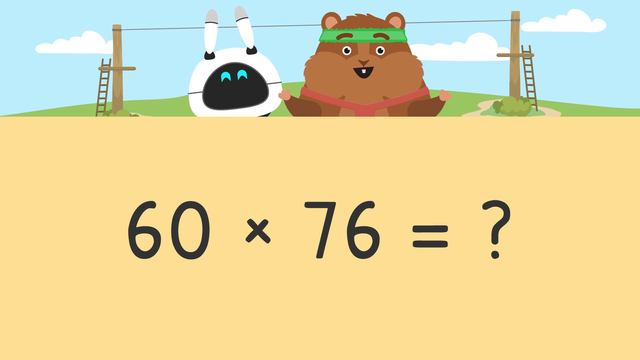Area Model Multiplication up to Three-Digits
- Multiplying a Multi Digit Number with 1-Digit Numbers
- Multiplying a 2-Digit Number with 1-Digit Numbers – Guided Practice
- Multiplying a 3-Digit Number with 1-Digit Numbers – Guided Practice
- Multiplying a Multi Digit Number with 1-Digit Numbers – Summary
- Frequently Asked Questions on How to Multiply a Multi Digit Number with 1-digit Number


Basics on the topic Area Model Multiplication up to Three-Digits
Multiplying a Multi Digit Number with 1-Digit Numbers
Are you ready to explore the world of multiplication? In this text, we'll delve into the fascinating method of multiplying a 2-digit or 3-digit number by a 1-digit number using an area model. This powerful technique will help you tackle multiplication problems with confidence. Once you learn how to use this method with 2-digit or 3-digit numbers, you will be able to use this method with multi-digit numbers, too!
Multiplying a 2-Digit Number with 1-Digit Numbers – Guided Practice
When you need to multiply a 2-digit number by a 1-digit number, the area model comes to the rescue.
The area model is a visual representation that simplifies the multiplication process.
Let's walk through a step-by-step example to illustrate how it works.
Let’s start with the first example: multiplying 38 by 5
Step 1: Setting up the area model
Begin by drawing a rectangle. Divide the rectangle into segments based on the number of place values in each number. In our example, 38 has two place values (tens and ones), so we split our rectangle into two parts. The number 5, being a 1-digit number, doesn't require further division.
Step 2: labeling the parts
Now, label each part with the expanded form of the factors. On the top, write "30 + 8," representing the number 38. On the left side, write the number 5.
Step 3: Finding partial products
The next step is to multiply each corresponding pair to determine the partial products. These are the results obtained when you multiply each part of one number with each part of the other number.
In our example, we start with the leftmost segment. Multiply 5 by 30 to get 150. Then, multiply 5 by 8, which equals 40.
Step 4: Summing up
To find the final answer, add up the partial products. In this case, the sum of the partial products is 190, which means that 38 multiplied by 5 equals 190.
Multiplying a 3-Digit Number with 1-Digit Numbers – Guided Practice
When you need to multiply a 3-digit number by a 1-digit number, the area model comes to the rescue. Let's walk through a step-by-step example to illustrate how it works.
Let’s look at the following example: Multiplying 245 by 3
Step 1: Setting Up the Area Model
Begin by drawing a rectangle. Divide the rectangle into segments based on the number of place values in each number. In our example, 245 has three place values (hundreds, tens, and ones), so we split our rectangle into three equal parts. The number 3, being a 1-digit number, doesn't require further division.
Step 2: Labeling the Parts
Now, label each part with the expanded form of the factors. On the top, write "200 + 40 + 5," representing the number 245. On the left side, write the number 3.
Step 3: Finding Partial Products
The next step is to multiply each corresponding pair to determine the partial products. These are the results obtained when you multiply each part of one number with each part of the other number.
In our example, we start with the leftmost segment. Multiply 3 by 200 to get 600. Then, multiply 3 by 40, which equals 120. Finally, multiply 3 by 5, resulting in 15.
Step 4: Summing Up
To find the final answer, add up the partial products. In this case, the sum of the partial products is 735, which means that 245 multiplied by 3 equals 735.
Multiplying a Multi Digit Number with 1-Digit Numbers – Summary
In summary, the area model simplifies the process of multiplying a 2-digit or 3-digit number by a 1-digit number. It's a valuable tool for learners of all ages, and with our example and guided practice exercises, you can enhance your multiplication skills effectively.
Remember, when multiplying a multi digit number by a 1-digit number, using area method is easy. You need to follow these steps:
| Step # | What to do |
|---|---|
| 1 | Setting up the area model |
| 2 | Labeling the parts |
| 3 | Finding partial products |
| 4 | Summing up |
For additional resources and exercises, visit our website to find 3 digit by 1 digit multiplication worksheets and more!
Frequently Asked Questions on How to Multiply a Multi Digit Number with 1-digit Number
Transcript Area Model Multiplication up to Three-Digits
What is Mr. Squeaks doing with all those supplies? Oh... Imani needs them to fuel the time machine so they can travel to the Stone Age! Before he gives them to Imani, he needs to calculate how many stones, clocks, and shoes he has. In order to do that, we will practice "Area Model Multiplication up to Three-Digits". An "area model is a rectangular model that helps us find the product of two numbers." Mr. Squeaks has five boxes with thirty-eight clocks in each. Let's help Mr. Squeaks calculate by multiplying thirty-eight times five. The first step is to set up our area model. Start by drawing a rectangle. Next, split it into the number of parts based on how many place values are in each number. Thirty eight has two place values...TENS and ONES, so we split our rectangle in two parts. Five has one place value so we don't break the rectangle into any more parts. Next, label each part by writing the factors in expanded form. The value of the three in the tens place is thirty and the value of the eight in the ones place is eight... so we label the TOP thirty plus eight. Then, we label the five on the LEFT SIDE. The second step is to multiply each corresponding pair to find the partial products. Partial products are the answers we get when each pair of factors is multiplied. In the box on the LEFT, we multiply five times thirty. (...) Remember, you can ignore the zeros at first to get fifteen... and then annex one zero to your answer. Five times thirty equals one hundred fifty. Now we multiply "five times eight" in the box on the RIGHT,(...) which equals forty. After we find all the partial products, the third step is to ADD them. This will give us the answer to our multiplication problem. One hundred fifty PLUS forty is one hundred ninety so (...) they have one hundred ninety clocks. Mr. Squeaks has eight boxes with seventy-six shoes in each. We need to find the product of seventy-six times eight. First, let's set up our area model by drawing a rectangle, (...) breaking it into parts, (...) and labeling it. When we label using expanded form, we have seventy plus six on the TOP and eight on the LEFT. The second step is to multiply each corresponding pair to find the partial products. Let's find the partial product for the box on the LEFT. What is eight times seventy? (...) Eight times seventy equals(...) five hundred sixty. Now let's find the partial product for the box on the RIGHT. Eight times six equals (...) forty-eight. Last, what is the sum of the partial products? (...) Five hundred sixty PLUS forty-eight equals(...) six hundred eight. That means Mr. Squeaks has six hundred eight shoes for the time machine. Last, Mr. Squeaks has three boxes with two hundred forty-five stones in each. We need to find the product of two hundred forty-five times three. The first step is to set up our area model (...) but how does this look with a three-digit number? We still label it using expanded form, (...) but now the model is broken into THREE parts since we are calculating a THREE-digit number. How do we label it? The TOP is labeled using the expanded form two hundred PLUS forty PLUS five... and the three goes on the LEFT. The second step is to multiply to find the partial products. This time, try multiplying on your own. The partial products are six hundred (...) one hundred twenty (...) and fifteen. Now, what do we do with the partial products? The last step is to find the sum of the partial products. (...) The sum of the partial products is seven hundred thirty-five, (...) which is the number of stones Mr. Squeaks has for the time machine. Remember(...) when we solve a multiplication problem using an area model, the first step is to "set up the area model". The second step is to "multiply each corresponding pair to find the partial products". The third step is to "find the sum of the partial products". Let's see if the time machine has enough fuel. It looks like it's working...
Area Model Multiplication up to Three-Digits exercise
-
Can you solve the multiplication problem?
HintsHave you multiplied each side of the area model?
After you have multiplied each side, your area model should look like this.
Have you added the partial products together?
Don't forget any zeros!
SolutionFirst of all, solve the equation on the left:
- 4 x 30 = 120
- 4 x 9 = 36
- 120 + 36 = 156
-
Can you complete the area model and solve the problem?
HintsMultiply each part separately. In this example 20 is being multiplied by 4, then 2 is being multiplied by 4.
At the bottom we need to add the partial products, and then complete the original multiplication problem.
SolutionMr. Squeaks had 5 boxes with 68 pencils in each. This is how the area model looks when it is completed.
- We multiply 5 by 60 to get 300.
- Then we multiply 5 by 8 to get 40.
- We then add 300 and 40 to get 340.
- 68 x 5 = 340.
-
Can you spot the mistakes in the area model?
HintsThink about how we partition a three digit number, has it been done correctly here? What should 248 be partitioned into?
What should the first digit in each of the three area model equations be?
Have the zeros been included on if necessary?
SolutionThe image above shows the mistakes highlighted.
- When partitioning a three digit number we need only the hundreds in the first box, so this should have been 200, both above the box and in the first box.
- 4 x 40 is 160, not 16. We can multiply 4 x 4 first to make it easier, but the 0 needs adding onto the end again.
- In the third box the first number should have been 4, as that is what we are multiplying 248 by.
- The final answer at the end is incorrect because of the mistakes in the area model. 248 x 4 = 992.
-
Can you find the correct answers to the multiplication problems?
HintsHave you partitioned the two or three digit number?
This example shows how we could set up 32 x 3 using an area model.
SolutionThe grid above has been filled in for the problem 42 x 7. 42 has been partitioned into tens and ones to give 40 and 2.
To solve:
- First of all we multiply 7 by 40 to get 280.
- We then multiply 7 by 2 to get 14.
- Now we need to add 280 and 14 to get 294.
- Therefore 42 x 7 = 294.
- 83 x 3 = 249
- 113 x 4 = 452
- 207 x 2 = 414
- 325 x 3 = 975
-
Can you complete the area model and find the answer?
HintsRemember to multiply 3 by the tens and the ones of the two digit number.
Add up your products to find the answer to the multiplication problem.
SolutionHere is the completed area model:
- 3 x 30 = 90
- 3 x 5 = 15
- We then add 90 and 15 to get 105.
- So, 35 x 3 = 105.
-
Can you solve the multiplication problems?
HintsRemember to partition your two or three digit number.
Add the partial products to find the answer.
SolutionFor the first problem:
- We need to partition 39 into 30 and 9.
- We then multiply 8 by 30 to get 240, and 8 by 9 to get 72.
- Next, add 240 and 72 to get 312.
- Therefore, 39 x 8 = 312
________________________________________________________
For the second problem:
- Partition 76 into 70 and 6.
- Multiply 4 by 70 to get 280, and 4 by 6 to get 24.
- Add 280 and 24 to get 304.
- Partition 122 into 100, 20 and 2.
- Multiply 6 by 100 to get 600, 6 by 20 to get 120, and 6 by 2 to get 12.
- Add 600, 120 and 12 to get 732.
- Partition 341 into 300, 40 and 1.
- Multiply 7 by 300 to get 2,100, 7 by 40 to get 280, and 7 by 1 to get 7.
- Add 2,100, 280 and 7 to get 2,387.