An Introduction to Translations
Learning text on the topic An Introduction to Translations
Translations in Math – Definition
In our daily lives, we often shift objects from one place to another without changing their shape or size, like sliding a book across a table. In geometry, this movement is known as a translation.
A translation in geometry is a transformation that moves every point of a figure the same distance in the same direction. It slides an object from one position to another without rotating, resizing, or deforming it.
Properties of Translations
- Direction: Translations move points in a straight line.
- Distance: Each point moves the same distance.
- Congruency: The original shape and its translation are congruent.
To have the most success with this topic, it is important that you are familiar with Ordered Pairs on the Coordinate Plane.
Translations – Step-by-Step Process
Below we have a triangle with vertices A(1,2), B(3,2), and C(1,4), and we want to translate it 2 units to the right and 3 units down.
| Step | Description | Example |
|---|---|---|
| 1 | Identify Original Coordinates | A$(1,2)$, B$(3,2)$, C$(1,4)$ |
| 2 | Determine the Translation | 2 units right, 3 units down |
| 3 | Apply the Translation to Each Point | A': $(1+2, 2-3) = (3, -1)$ B': $(3+2, 2-3) = (5, -1)$ C': $(1+2, 4-3) = (3, 1)$ |
| 4 | Plot and Label the Translated Figure |  |
| 5 | Verify Congruency | Check that original and translated figures are congruent |
Translation Notation
In translation notation, we describe exactly how to shift each point. We use $ (x, y) \rightarrow (x+a, y+b) $, where:
- $ x, y $ are the original points.
- $ a $ is how far we move left or right.
- $ b $ is how far we move up or down.
For example, $ (x, y) \rightarrow (x+3, y-2) $ means move every point 3 units right and 2 units down.
| Original Point | Translation Notation | Translated Point |
|---|---|---|
| $ (2, 3) $ | $ \rightarrow (x+4, y+1) $ | $ (6, 4) $ |
| $ (5, 5) $ | $ \rightarrow (x-3, y-2) $ | $ (2, 3) $ |
| $ (1, 2) $ | $ \rightarrow (x+2, y+5) $ | $ (3, 7) $ |
| $ (4, 4) $ | $ \rightarrow (x+1, y-1) $ | $ (5, 3) $ |
| $ (3, 1) $ | $ \rightarrow (x-2, y+3) $ | $ (1, 4) $ |
Labeling a Translated Figure
When we move geometric shapes, like sliding a square on graph paper, we use special labels to keep track of the new positions. This is where 'prime' labels come in handy.
- Easy to Spot: By adding a little mark, called a 'prime' (like A'), we can see which points have moved. It's like tagging something with a sticky note.
- Matching Points: Prime labels help us match the original points with their new spots. If point A moves, it becomes A'. This way, we know A and A' are related.
- Simple and Clear: Using prime labels is an easy way to show which shape has moved and where it has gone. It keeps our diagrams tidy and easy to understand.
Using prime labels is like putting a "Moved!" sign on our shapes. It's a simple, clear way to show where they've gone.
Translations – Guided Practice
Let’s work through the following translation of a triangle on a coordinate grid.
Not only can you perform isolated translations, but also a sequences of translations can be done to move a figure further, while still keeping it congruent.
Translations – Exercises
To practice translating, find a sheet of graph paper to practice with the following exercises.
For some more advanced transformations, sequences of reflections and translations can be done to a figure, and it will still be congruent!
Translations – Summary
Key Learnings from this Text:
Translations slide a shape in a straight line without rotating or resizing.
Each point in the shape moves the same distance and direction.
The original and translated shapes are congruent.
Understanding translations helps visualize how shapes interact within a space.
Translations – Frequently Asked Questions
An Introduction to Translations exercise
-
Understand the definition of a translation.
HintsLook at the words you know in the definition to help you find the meaning of a translation.
- resize
- flip
- turn
- slide
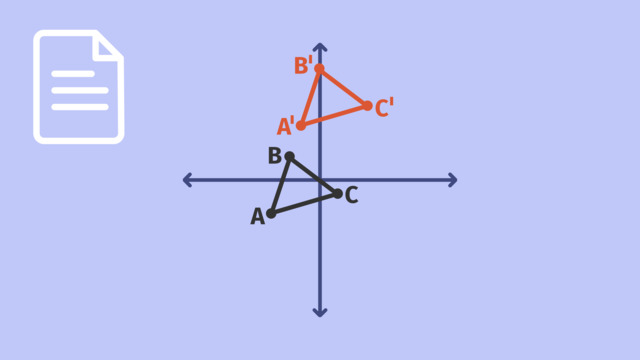
Look carefully at figure ABC in the header. What do you notice about figure A'B'C'? It is a different size? Did the image flip? Has it been turned? Did the figure slide?
SolutionA translation is sliding a shape across a plane without rotating or flipping it.
When shapes are translated, they can go left or right, and up or down. In example seen here, the image was translated 9 units down.
-
Identify labels and coordinates of a translated figure.
HintsWhen we move geometric shapes, like sliding a square on graph paper, we use special labels to keep track of the new positions. This is where prime labels come in handy.
In this example you can see that figure ABC was translated and is now labeled A'B'C'.
SolutionThe new figure is labeled here with E'F'G'H'.
-
Identify the translation a figure underwent.
HintsBe sure to count each unit carefully when determining the translation. Each coordinate moved on the graph is considered 1 unit.
By adding a little mark, called a prime (like A'), we can see which points have moved.
Remember to find the rule of each point translated to its corresponding point. For example, point A is translated to A' (A prime).
SolutionTriangle ABC was translated Right 5 units, Down 3 units to triangle A'B'C'.
-
Apply your knowledge of translations to translate a point based on the directions.
HintsOne way to translate a coordinate is to count in the given direction on a graph.
$(-2,3)$ translated 4 units right and 2 units down ends up on $(2,1)$.
Another way to translate a coordinate is to add or subtract the $x$ and $y$ values.
$(-2,3)$ translated 4 units right and 2 units down $(-2+4, 3-2)\rightarrow(2,1)$
Solution- Original: (-4, 2) Translated 4 units right, 2 units down: (0, 0)
- Original: (-4, 0) Translated 4 units right, 2 units down: (0, -2)
- Original: (-1, 0) Translated 4 units right, 2 units down: (3, -2)
- Original: (-1, 2) Translated 4 units right, 2 units down: (3, 0)
-
Identify which transformation is a translation.
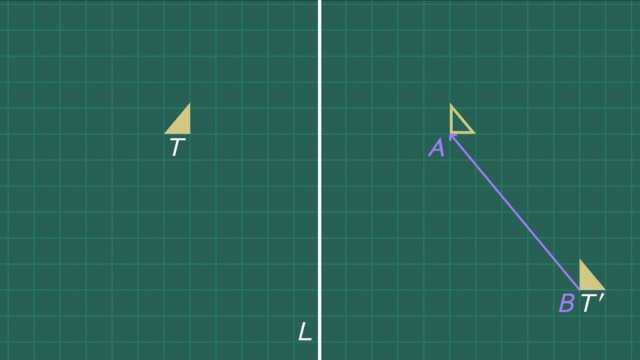
HintsA translation is when you slide a shape to a different spot without turning or flipping it. Imagine moving a piece of paper straight across your desk without turning it over or spinning it around. The shape still looks the same, just in a new place.
In the image here figure ABCD has been translated right 6 units and up 2 units to A'B'C'D'.
When a shape is translated, the size and orientation of the shape stay the same.
SolutionThese triangles have been translated because they can slide from one to the other without changing directions or size. These shapes are congruent.
-
Translate a figure and label the new coordinates.
HintsDon't forget to add a comma (,) between the coordinates in the translated figure.
It may help you to draw this on graph paper and count the units to find the translated figure.
You can also use the translation notation to calculate the coordinates of the translated figure.
The rule, $ \rightarrow (x-1, y-2) $, means that the figure will move left 1 unit and then down 2 units.
SolutionThe translated points will be:
X' = (-1,-2)
Y' = (-3,0)
Z' = (-1,1)