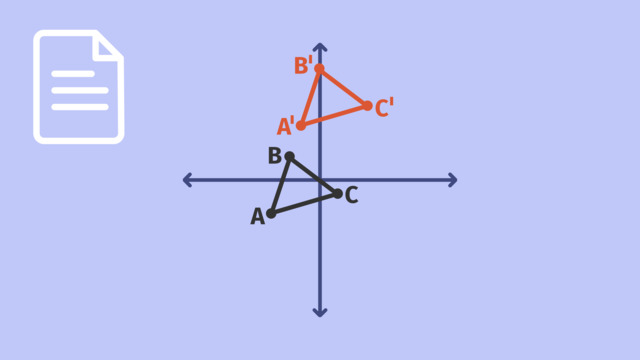
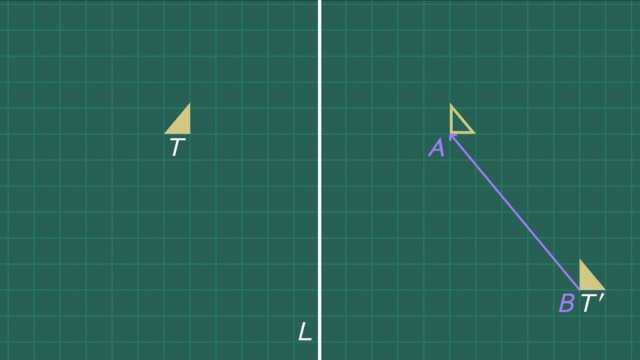
Translations of Lines


Basics on the topic Translations of Lines
After this lesson, you will be able to use a vector to translate a line, and visualize the possible results.
The lesson begins by teaching you to translate a line along a vector to create a parallel line. It leads you to learn to translate a line along a vector to create a line that coincides with the original. It concludes with the idea that, given a line and a point not on it, there is exactly one line through the point that is parallel to the original line.
Learn about translations and parallel lines by helping Akio become a zen garden master!
This video includes key concepts, notation, and vocabulary such as translation (moving a geometric object without changing its size or shape); vector (a directed line segment which shows us the length and direction of the translation); image (the object which results from the translation of an original); prime notation (if the original line is ‘L’, the image after translation is ‘L’’, that is, ‘L’ prime); parallel lines (two lines in a plane which don’t intersect); and coincident lines (two lines in a plane which intersect in all their points).
Before watching this video, you should already be familiar with the idea that translation is moving an object along a vector to create a new object that has the same size and shape; the idea that lines in a plane can be intersecting or parallel; and the idea that coincident lines overlap each other completely.
After watching this video, you will be prepared to learn how to transform lines and other objects using translation, rotation or reflection.
Common Core Standard(s) in focus: 8.G.A.1 A video intended for math students in the 8th grade Recommended for students who are 13 - 14 years old
Transcript Translations of Lines
Master Shinichi and his student Akio are carefully constructing a beautiful zen garden. They apply geometric principles to the natural materials of sand, wood, and stone. Akio has a few challenges to complete before he can go forth and build his own garden. He needs to discover the mystery of translations of lines. First, Akio must solve an ancient riddle. The challenge is to find a translation of this line which is NOT parallel to it. How can we TRANSLATE a line so that the IMAGE is NOT parallel to the original line? Is that even POSSIBLE? Consider line 'L' and vector 'u'. Vector 'u' is a DIRECTED LINE SEGMENT that tells us how FAR we want to move line 'L', and the DIRECTION we want to move it. Let's translate line 'L' ALONG the vector 'u'. This give us the NEW line, 'L' prime. L' prime is the IMAGE resulting from the translation of 'L'. Point 'P' MAPS to the point 'P' prime, and in fact, ALL the points on the line move the SAME distance in the SAME direction. L' prime is PARALLEL to 'L'. But the riddle asks for a translation that gives us an IMAGE that's NOT parallel to 'L'. Can you think of a way to CHANGE this translation so that the image is NOT parallel to the original? If we change the LENGTH of the vector, the image is still parallel to the original. Let's change the DIRECTION of the vector. Almost there, yes! What happened? Notice that we made vector 'u' PARALLEL to the original line. This translation of 'L' ALONG vector 'u' gives us an IMAGE that perfectly overlaps the original! We say this image COINCIDES with the original. The IMAGE and the ORIGINAL intersect in an INFINITE number of points, meaning that they are the same line! And thus are NOT parallel to each other. Woah, mind blown! The only translation of a line which is NOT parallel to the original is a translation which gives the original line as its image! And so all translations of a line are parallel to the original. Now Akio is ready for the next challenge. How many lines can we draw through THIS point, that are parallel to THIS line? Let's experiment. There are an infinite number of lines through point 'Z'. But nearly all of them intersect line 'L'. All except for ONE. This one! There is exactly one line through 'Z' that is parallel to 'L'. No more and no less. Thus, we know that given ANY line, and a point NOT on the line, there is ONE line parallel that goes through the given point. While Akio applies his discoveries to his work in the zen garden, let's review what we've learned. Any translation of a line along a vector gives us a line parallel, except when we make the vector parallel to the original line, in which case the image coincides with, or is the same as, the original. Additionally, given a line and a point not on it, there is exactly one line parallel that goes through the given point. With his newfound wisdom, let's see what Akio is creating. Wow! Looks like he has truly become a master.