Unit Rate as the Constant of Proportionality


Basics on the topic Unit Rate as the Constant of Proportionality
After this lesson, you will be able to identify the unit rate, find the constant of proportionality, and use it to determine the missing value in proportional relationships.
The lesson begins by calculating the unit rate. It leads you to learn that when a unit rate remains the same, it is called the constant of proportionality. It concludes by solving proportional relationships.
Learn about unit rates as the constant of proportionality by helping Isaac reach his goal of making 1,000 gold nuggets!
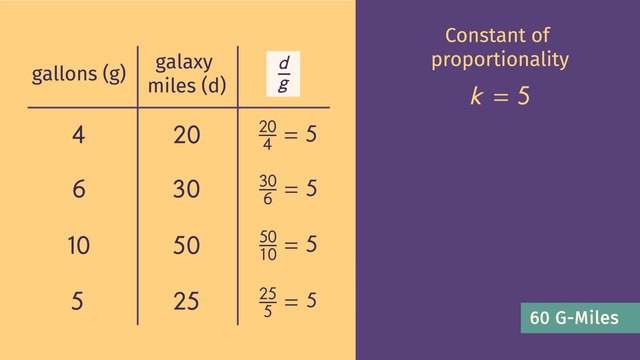
This video includes key concepts, notation, and vocabulary such as the unit rate (a comparison of two different quantities), constant of proportionality, (when the unit rate remains the same), and proportional relationships (a constant ratio, or the unit rate).
Before watching this video, you should already be familiar with finding unit rates by dividing the two quantities in a ratio, using the unit rate to illustrate the constant of proportionality, and proportional relationships.
After watching this video, you will be prepared to write equations that represent proportional relationships.
Common Core Standard(s) in focus: 7.RP.A.2 and 7.RP.A.2c A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
Transcript Unit Rate as the Constant of Proportionality
It's 1682 and Gottfried Leibniz has just rocked the math world by introducing a new kind of mathematics called calculus! But not everyone is happy with Gottfried's success. Isaac Newton wants to quickly publish his paper to show that he's been using calculus for years. It'll cost Isaac 1,000 gold nuggets to print his paper. Where will Isaac come up with all those gold nuggets? Luckily, he's just invented a machine that can turn regular rocks into gold! For Isaac to make enough gold to get his paper printed, we'll need to help him interpret unit rates as the constant of proportionality. Isaac documents the time it takes his machine to convert rocks to gold. Here is a table, showing us the relationship between the hours that have passed and the amount of gold nuggets produced. Isaac needs to make 1,000 nuggets, but that's not on the table. So, what information does this table give us in order to figure out how long it'll take to produce enough gold? From the table we can calcuate the unit rate to see how fast this machine works. To caculate the unit rate we take the ratio of nuggets to hours for each pair of numbers. Then we simplify each fraction. 4 over 1 is 4. 12 over 3 is also 4. And the remaining fractions... reduce to 4 as well! Because the unit rate remains the same it is a CONSTANT. For this reason, the unit rate is also called the constant of proportionality. We represent the constant of proportionality with the letter 'k.' Isaac's machine is running smoothly, producing gold at a constant rate of 4 nuggets per hour. Isaac wonders: If he runs the machine for 48 hours, will he reach his goal of 1,000 nuggets? Using the constant of proportionality,4 nuggets per hour, we can set-up a proportional relationship. Replacing hour with 48 and solving for nuggets, we see that 48 times 4 equals 192 nuggets. That's not even close to 1,000 nuggets yet! And even worse, the machine stops working! Isaac repairs it, but his newly documented ratio table of hours and nuggets shows different outcomes. Are the proportions shown actually constant? Like before, we set-up the ratios of nuggets per hour, then simplify each ratio. Notice all ratios simplify to 3 nuggets per hour. Therefore, we have a new constant of proportionality. If Isaac runs the machine for 48 more hours, will he make it to 1,000 nuggets? Just like before, we can multiply the hours by the constant of proportionality to get the total nuggets. This means 48 times 3 is 144 nuggets. Adding these nuggets to the earlier 192 nuggets means Isaac only has 336 nuggets so far. Ugh...he still needs to make 664 nuggets in order to get to 1000. Isaac improves his machine and takes a real risk by cranking the machine up to produce 8 nuggets per hour! Using the earlier set-up, how long will it take Isaac to produce the total 664 remaining nuggets? We know the constant of proportionality: 8 nuggets per hour. Therefore we can divide the total 664, by the constant of proportionality, 8, giving us 83 hours. Isaac runs his machine day and night, for 83 hours. Luckily, the machine doesn't malfunction, and Isaac finally reaches his goal of producing 1000 nuggets. Now Issac can publish his calculus paper and take the world by storm! Let's review Isaac's work with unit rate as the constant of proportionality. Given a table, we can always simplify each ratio pair to find the unit rate. When the unit rate remains the same it is called the constant of proportionality, 'k'. Multiply or divide by the constant of proportionality, to solve problems depending upon the information you're given. So, did Isaac's mastery of the constant of proportionality bring him the fame he desired? Oh no, all that work and it was just a dream. Hopefully he'll soon get the recognition he deserves.