Representing Proportional Relationships with Equations - complex example

Basics on the topic Representing Proportional Relationships with Equations - complex example
After this lesson, you will be able to use tables, graphs, and equations from real-world situations to solve proportional relationships.
The lesson begins by teaching you how to find the constant of proportionality from a table. It leads you to writing and solving proportional relationships. It concludes with using a graph to write and solve the equation of a proportional relationship.
Learn about solving proportional relationships by helping Chad’s customers get to where they want to go in space!
This video includes key concepts, notation, and vocabulary such as the constant of proportionality (a ratio between two quantities that remains the same) and proportional relationships (a relationship between two equal ratios).
Before watching this video, you should already be familiar with the constant of proportionality, its relation to the unit rate, and graphing the correct independent and dependent variables.
After watching this video, you will be prepared to learn how to use the graph of an equation to find other ordered pairs that fit the equation; and how to use the constant of proportionality to identify the slope of an equation.
Common Core Standard(s) in focus: 7.RP.A.2a A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
Transcript Representing Proportional Relationships with Equations - complex example
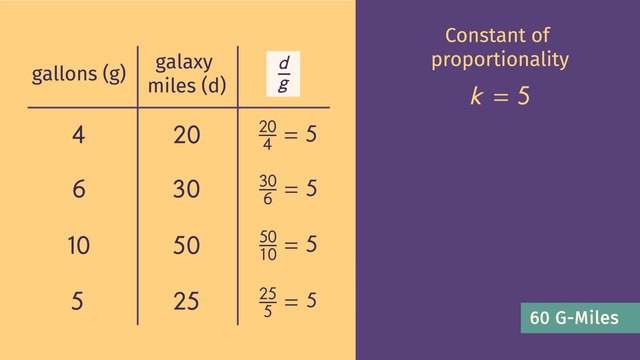
With new advances in technology, it's easy to get around in space nowadays. As long as you're careful not to run out of gas. The only station in this part of the galaxy is Chad's Gas and Snacks, run by a friendly face that is willing to help you with anything you need. To help Chad's customers get where they need to go, you need plenty of petrol and the ability to find the equations of proportional relationships. Here comes Chad's first customer of the day! It's a minister on his way to officiate a wedding, and he's both out of gas and running late. The wedding is 60 galaxy miles away, but the minister doesn't know how much gas his rent-a-shuttle needs to get there. Luckily, the spacecraft has records of its past fuel use. Let's see if we can use that data to help the minister. The first column in this table notes the gallons of gas used by the minister's rent-a-shuttle, 'g', and the second column shows the distance traveled, 'd', in galaxy miles. For example, it took 4 gallons for the rent-a-shuttle to travel 20 galaxy miles, and 6 gallons to travel 30 galaxy miles. Let's create another column to look at the ratio of galaxy miles to gallons of gas. 20 divided by 4 equals 5. 30 divided by 6 equals 5, and so on. The relationship between gallons of gas used and galaxy miles traveled is a proportional relationship, and our constant of proportionality, represented by k, is 5. That means the ratio of 'd' to 'g' will always be equal to 5. We can write this as the equation 'd' over 'g' equals 5, which is the same as 'd' equals 5g. So, how many gallons of gas does the minister need to get to the wedding? Since the wedding is 60 galaxy miles away, we can plug that in for 'd'. Solving for 'g' gives us 'g' equals 12 gallons. Chad gets the minister his gas, and some munchies for the road. He's all fueled up and ready to officiate! Oh look, it's another customer rolling up and in a very snazzy ship! The groom is worried that he won't be able to make it to the wedding, even if he fills up his tank. His tank can only hold 25 gallons, and the wedding is 60 galaxy miles away. The groom doesn't know what gas mileage his ship gets, but the dashboard includes a graph comparing the distance traveled to gas used. On this graph, the horizontal axis represents the gallons of gas used, and the vertical axis is the distance traveled, in galaxy miles. This graph represents a proprotional relationship, since it's a straight line through the origin. If we can find the constant of proportionality, then we can find an equation that relates gas and distance. Since it's the CONSTANT of proportionality, we can use any point on the line to find it. Using the point (5,15), we get 'k' equals 15 divided by 5, which equals 3. That means the groom's spaceship travels 3 galaxy miles per gallon. Since the constant of proportionality is the same for any values of 'd' and 'g', we can write the equation 'd' over 'g' equals 3. Since the groom will fill up his gas tank with 25 gallons of gas, we can plug in 25 for 'g'. That gives us 'd' equal to 3 times 25, which is 75 galaxy miles. That means a full tank will be sure to get him to the wedding, which is only 60 galaxy miles away. The groom is so relieved and grateful that he invites Chad along for the wedding! Who could say no to that?! Proportional relationships can be represented in graphs, tables, and equations. If we're given a graph or a table with variables 'x' and 'y', we can find the corresponding equation by finding the constant of proportionality, represented by k. That let's us write the equation 'y' over 'x' equals 'k.' Another way to write that is 'y' equals kx. Looks like another customer in need came by while we were away...where are you, Chad?













