Understanding Equations

Basics on the topic Understanding Equations
An equation is a statement of equality between two algebraic expressions. A very crucial skill in solving word problems is learning how to represent the unknown value or values with the correct algebraic expressions and relate the expressions to form an equation based on the given conditions. To determine the solution, simply perform the inverse operations with respect to the equation formed. To verify whether a number or value is a solution to the equation, just substitute the number to the variable in the equation and check to see whether the resulting number sentence is true. Learn about algebraic expressions and equations by helping Phineas win a bet with his friends on completing a trip around the world in just 80 days. Common Core Reference: CCSS.MATH.CONTENT.6.EE.A.2.C
Transcript Understanding Equations
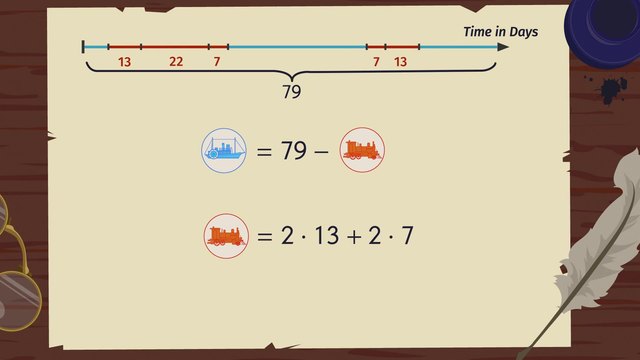
Phineas Fogg has just received an exclusive advertisement for the new trans-Siberian railway. He thinks that he can now complete a trip around the world in just 80 days! He’s so confident, in fact, that he makes a bet with his buddies. In order to plan his trip, Phineas will need to understand expressions and equations. Phineas wants the total length of the trip to be 79 days, you know, just in case something goes awry. He'd like to take trains and steamers as his primary modes of transportation. Over land, he’ll take trains. Over sea, he’ll take steamers. It’d be silly to do it the other way 'round. He figures that there will be 5 legs of his trip by train. Two of the legs will be exactly 13 days long, two more will be 7 days long and one leg will be a whopping 22 days long! If the rest of the trip is to be done by steamer, how many days does Phineas have left? We know that Phineas wants his trip to last 79 days, so we can simply subtract the number of days he plans to travel by train from 79, giving us the number of days he's able to travel by steamer. Now, we need to calculate the total number of days Phineas Fogg plans to travel by train. To do this, we have to add the duration, in days, for each of the 5 legs of the trip he plans to travel by train. There are two legs that are 13 days long, as well as two legs that are 7 days long. We can multiply 13 and 7 by 2, since each duration occurs twice. The final leg of the trip by train is the longest at 22 days, so we just add that to find our grand total. We can substitute this into our original equation and then solve. Remember! You have to distribute the negative sign to all the terms in the parentheses. Now, just complete the process by using PEMDAS. Remember to solve from left to right, and we have our answer! 17 Days. Now that we know how long the trip should take, we should probably help Phineas figure out how much the trip'll cost since no one’s made of money. We need to know how many of each kind of ticket Phineas needs to purchase, as well as the cost of the different modes of transportation. If each train ticket costs two-thirds the price of a steamer ticket... We can represent the train ticket price in terms of the steamer ticket price. Each steamer ticket will cost 45 pounds, so we can substitute this value here and here. Phineas will need 5 train tickets and 3 steamer tickets. Let's evaluate what we have. 3 times 45 is 135. 5 times two-thirds is 10 over 3. 10 over 3 times 45 is 150, and 135 plus 150 gives us our grand total and how much money Phineas needs for the tickets: 285 pounds sterling. Satisfied that he'll have the funds and the time to make it around the world in 80 days, Phineas sets off on his journey. Let's check on his progress.
Understanding Equations exercise
-
Determine the number of days Phineas Fogg will travel by steamer.
HintsSubtract the number of days which Phineas travels by train from the total number of the days of his trip.
We have $23-(4+12)=23-16=7$, or $23-(4+12)=23-4-12=19-12=7$.
SolutionTo determine the time Phineas Fogg has to travel by steamboat, we must subtract the number of the days Phineas travels by train from $79$ days.
He travels by the train during five legs of his trip. Two legs take $13$ days, or $2\cdot 13$ days. Two legs take $7$ days, or $2\cdot 7$ days. And one leg takes $22$ days. That is a total of $2\cdot 13+2\cdot7+22=62$ days by train.
Now we subtract this number from $79$ to get $79-62=17$ days that he will travel by steamboat.
-
Examine the costs of Phineas Fogg's trip.
HintsAdding a value to itself twice is the same as multiplying it by 2: $x+x=2\cdot x$.
Similarly, adding a value to itself three times is the same as multiplying it by 3: $x+x+x=3\cdot x$.
You have to add the price of the steamboat tickets and the train tickets together.
Pay attention to PEMDAS.
SolutionPhineas needs three steamboat tickets for the price of $S$, and five train tickets for the price of $T$. So the cost $C$ of the all of his tickets is $C=3\times S+5\times T$.
The relation between the price of the steamboat tickets and the price of the train ticket is given by $T=\frac23\times S$.
This means that $C=3\times S+5\times T=3\times S+5\times (\frac23\times S)$.
Plug in the known price for one steamboat ticket:
$\begin{array}{rcl} C&=&3\cdot 45+5\cdot \frac23 \cdot 45\\ &=&135+150\\ &=&285 \end{array}$
So we can see that Phineas needs to pay a total of $285$ pounds on tickets for his trip.
-
Identify the solutions of the equations.
HintsThe keywords each or for one indicate multiplication.
Take a look at the following example:
If $1$ liter of milk costs $1.20$ pounds, then $5$ liters cost $5\times1.20=6$ pounds.
If you buy, in addition, $6$ bread rolls at $0.50$ pounds each, you have to pay
$5\times 1.20+6\times 0.50=6+3=9$ pounds altogether.
Remember PEMDAS: multiplication comes before addition.
SolutionCoffee and muffin
- A coffee costs $2.50$ pounds. So we get $4\times 2.50$ pounds for $4$ coffees.
- A muffin costs $2$ pounds. This leads to $3\times2$ pounds for $3$ muffins.
- To receive the whole price, these expression have to be added: $4\times 2.50+3\times 2=10+6=16$.
$~$
Tickets and ice
- A ticket costs $4$ pounds. So $3$ tickets $3\times 4$ pounds.
- An ice costs $1.50$ pounds and hence $4$ ices $4\times1.50$ pounds.
- These Terme are added to reach the whole price: $3\times 4+4\times1.50=12+6=18$.
$~$
Taco and coke
- A taco costs $4.50$ pounds, so $2$ tacos cost $2\times 4.50$ pounds.
- If a coke costs $2.50$ pounds, $4$ cokes cost $4\times 2.50$ pounds.
- Now these Terme must be still added: $2\times 4.50+4\times2.50=9+10=19$.
$~$
Bagel and tea
- A bagel costs $1.20$ pounds and with it $5$ bagel $5\times 1.20$ pounds.
- A tea costs $3$ pounds, then $4$ teas $4\times3$ pounds.
- Now these Terme can be added: $5\times 1.20+4\times 3=6+12=18$.
-
Examine the equation and solve it.
HintsPhineas drinks $2$ tea each day.
You have to multiply the price of each food by the number of days.
Phineas spends a little more than $50$ pounds. So he has a little less than $50$ pounds at disposal.
SolutionFirst, we calculate the total costs for the mango sticky rice and Thai iced tea separately:
- Mango sticky rice: $30\times 0.75=22.50$
- Thai ice tea: $30\times 2\times 0.50=30$
He would like to know how much money he has at his disposal to spend on other foods. To figure this out, he subtracts $52.50$ from $100$ pounds: $100-52.50=47.50$.
So we see that Phineas has $47.50$ pounds to spend on other foods.
-
Decide if the statement is true or false.
HintsAn expression is a meaningful arrangement of numbers, variables, and operation signs.
A number is an expression.
The addition, subtraction, multiplication, or division of expressions is an expression too.
In an equation, there are expressions on the left-hand side as well as the right-hand side of an equals sign.
SolutionIn general an expression is a meaningful arrangement of numbers, variables, and operations, as well as parentheses.
An equation contains an equals sign.
In an equation, there are expressions on the left-hand side as well as the right-hand side of an equals sign.
A single number is an expression.
Here are some examples of expressions:
- $2\cdot 13+2\cdot 7+22$
- $79-62$
An example of an equation is $3\cdot 45+5\cdot \frac23\cdot 45=285$.
-
Find the solution to the word problem.
HintsThe first monkey throws $5$ balls to the second one. Then the elephant comes into play; he takes a ball.
After $5$ balls have been thrown, the elephant takes one. Then the juggling $4$ balls before the first monkey throws him a new ball.
After the first $5$ balls, the elephant is always taking $1$ ball from the second monkey after the first monkey throws him a ball.
SolutionHow can we find the number of balls the elephant throws into the net if the first monkey has $25$ balls to throw? Let's see what is going on step-by-step:
- The first monkey throws the first ball to the second monkey. Now the second monkey is juggling $1$ ball, and the first monkey has $24$ balls left to throw.
- The first monkey throws the second ball to the second monkey. Now the second monkey is juggling $2$ balls, and the first monkey has $23$ balls left to throw.
- The first monkey throws the third ball to the second monkey. Now the second monkey is juggling $3$ balls, and the first monkey has $22$ balls left to throw.
- The first monkey throws the fourth ball to the second monkey. Now the second monkey is juggling $4$ balls, and the first monkey has $21$ balls left to throw.
- The first monkey throws the fifth ball to the second monkey. Now the second monkey is juggling $5$ balls, and the first monkey has $20$ balls left to throw.
Now, every time the first monkey throws the second monkey a ball, the elephant will take a ball and throw it into the next. Since there are $20$ balls left to throw, the elephant will do this $20$ times. And so that is $20$ balls in the net plus $1$ ball from the initial $5$ balls. All together, there are $21$ balls in the net by the time the animals stop and take a bow.
What about when the first monkey has $b$ balls to throw?
Well, we have the initial number of balls $b$ the first monkey has to throw. Then, after the first four balls are thrown, a ball gets thrown into the net every time the first monkey throws a ball to the second monkey. After all $b$ balls have been thrown, there are 4 left over which have not been thrown into the net. So every ball but four end up getting thrown into the net, meaning that $b-4$ balls end up in the net in the end.