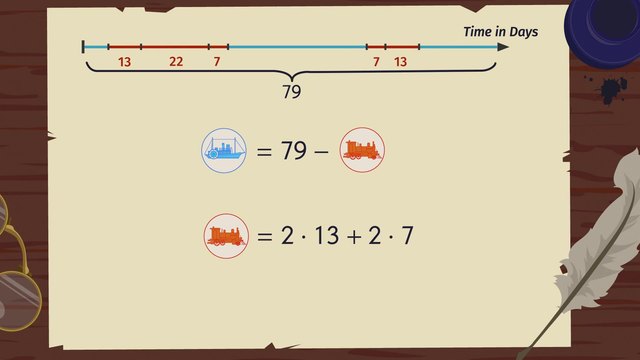
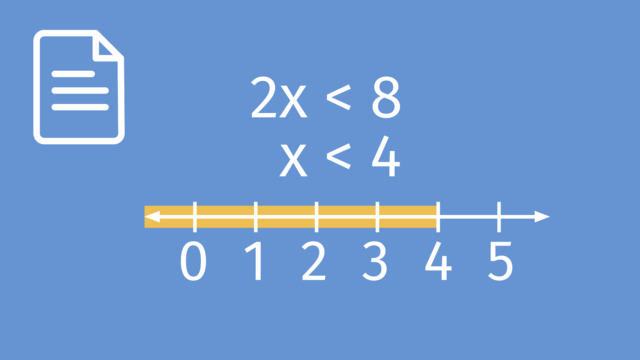Solving Inequalities
Learning text on the topic Solving Inequalities
Introduction to Solving Inequalities
Inequalities are fundamental components of mathematics and everyday decision-making. They express the relationship between two values, indicating that one is greater than, less than, equal to, or not equal to another. These comparisons form the basis of problem-solving across various disciplines, from personal budgeting to scientific research.
Understanding Inequalities – Definition
Inequalities are mathematical expressions that compare two values, showing that one value is greater than (>) or less than (<), greater than or equal to (≥), or less than or equal to (≤) another.
| Inequality Sign | Description |
|---|---|
| $ > $ | greater than |
| $ < $ | less than |
| $ \geq $ | greater than or equal to |
| $ \leq $ | less than or equal to |
Solving Linear Inequalities – Examples
Let's solve a linear inequality together:
Given: $3x - 5 ≤ 2x + 10$
Steps:
- Subtract $2x$ from both sides: $x - 5 ≤ 10$.
- Add $5$ to both sides: $x ≤ 15$.
Result: $x$ must be less than or equal to $15$.
When solving inequalities, remember to reverse the direction of the inequality sign when multiplying or dividing both sides by a negative number. This ensures that the inequality remains true.
Let's solve another linear inequality:
Given: $-4x + 3 < 15$
Steps:
- Subtract $3$ from both sides: $-4x < 12$.
- Divide both sides by $-4$, remembering to reverse the inequality sign due to dividing by a negative number: $\frac{-4x}{-4} > \frac{12}{-4}$.
- Simplify: $x > -3$.
Result: $x$ must be greater than $-3$.
Solving Inequalities – Practice
Let’s practice some more!
Solving Inequalities – Summary
Key Learnings from this Text:
- Inequalities help us express relationships between two values.
- They come in various forms, including linear, quadratic, absolute value, and more.
- Solving inequalities often mirrors solving equations, with the added rule of flipping the inequality when multiplying or dividing by a negative number.
- Shading on a graph represents the solution set of an inequality.
For more practice with inequalities, check out our interactive exercises and video tutorials that make learning engaging and fun!
Solving Inequalities – Frequently Asked Questions
Solving Inequalities exercise
-
What does each inequality mean?
Hints$<$ means less than and $>$ means greater than.
$\leq$ means less than or equal to and $\geq$ means greater than or equal to.
We can write x is greater than 9 as $x > 9$ or $9 < x$.
Solution$x > 2$ means $x$ is greater than $2$
$x \leq 4$ means $x$ is less than or equal to $4$
$x \geq 4$ means $x$ is greater than or equal to $4$
$x < 2$ means $x$ is less than $2$
$5 > x$ means $x$ is less than $5$
$5 < x$ means $x$ is greater than $5$
-
True or False?
HintsTo test the inequality, replace the variable (the letter) by the number.
For example, does $a = 5$ satisfy the inequality $a < 7$?
Replace $a$ with $5$, giving $5 < 7$.
$5$ is less than $7$ so this is true.
You can use a number line to help you. Numbers to the left are less than numbers to the right.
In the last example, $5 < 7$ because $5$ is to the left of $7$.
We can also say that, $7 > 5$ because $7$ is to the right of $5$.
Be careful with negative numbers. For example $-4$ is less than $-1$ as $-4$ is to the left of $-1$.
SolutionThe inequality $x > 5$, is true when $x$ is $9$?
The inequality $y < 2$, is false when $y = 4$?
When $m > 8$, it is false that $m = 8$ satisfies the inequality?
The inequality $t \geq -5$ is true when $t$ is $-3$?
When $p \leq 7$, it is true that $p$ is $7$ satisfies the equation?
-
Solve an inequality with a negative variable.
HintsSolving inequalities is often similar to solving equations.
Remember to reverse the inequality sign when dividing by a negative.
For example: $-5t > 35$
Divide by $-5$ and reverse the inequality giving:
$t < -7$
Solution$-6p - 3 > 15$
Add $3$ to both sides.
$-6p > 18$
Divide both sides by $-6$, remember to reverse the inequality sign when dividing by a negative.
$p < -3$
Result: p is less than $-3$.
-
Solve the inequality.
HintsSolving inequalities is often similar to solving equations.
If the inequality has variables on both sides, we start by addressing this. Remove the smaller variable first by carrying out the inverse operation.
For example: $7y - 6 \geq 2y + 4$.
Step one would be to subtract $2y$ on both sides.
This gives $5y - 6 \geq 4$.
SolutionSolve $5m - 8 \leq 3m + 4$
Step one: Subtract $3m$ on both sides.
$\bf{2m}$ $- 8 \leq 4$
Step two: Add $\bf{8}$ to both sides.
$\bf{2m \leq 12}$
Step three: Divide both sides by $\bf{2}$.
$m \leq$ $\bf{6}$
Result: $m$ is less than or equal to $\bf{6}$.
-
Solve the inequality.
HintsStart with the inequality you are solving.
Remember to state the result at the end. This means that you write the inequality in words.
For example, $t < 7$ means $t$ is less than $7$.
SolutionStart with the inequality:
$2x + 9 < 15$
Subtract 9 from each side:
$2x$ $< 6$
Divide both sides by 2:
$x$ $< 3$
State the result:
$x$ is less than 3.
-
Solve an inequality with a bracket.
HintsIt is helpful to expand the bracket first.
$x$ and $1x$ are equivalent.
Remember to use inverse operations to solve the inequality.
SolutionSolve $5x + 10 \geq 4(x + 3)$
$5x + 10 \geq 4x + 12$
$1x + 10 \geq 12$
$x \geq 2$