The Graphs of Horizontal and Vertical Lines

Basics on the topic The Graphs of Horizontal and Vertical Lines
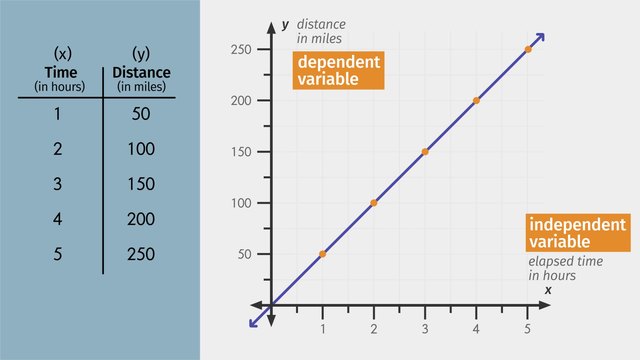
A horizontal line is parallel to the x-axis and is perpendicular, as well as intersects, the y-axis. The slope of a horizontal line is always zero, as its change in y is always zero. A vertical line, on the other hand, is parallel to the y-axis and is perpendicular, as well as intersects, the x-axis. The slope of a vertical line is undefined, as its change in x is always zero, thus giving a slope with zero in the denominator. See how Stephanie applies these properties to plot movements for her game character 8-BitBot in navigating vertical and horizontal direction in her computer gaming program. Common Core Reference: CCSS.MATH.CONTENT.8.FA.3
Transcript The Graphs of Horizontal and Vertical Lines
Stephanie is really into old school computer gaming.
So she's learning how to program to make her own game.
In order for Stephanie to make her character, 8bitbot, move along the correct paths, she needs to investigate the graphs of horizontal and vertical lines.
Let's start by first setting up a coordinate plane.
We'll draw and label the x-axis and then the y-axis.
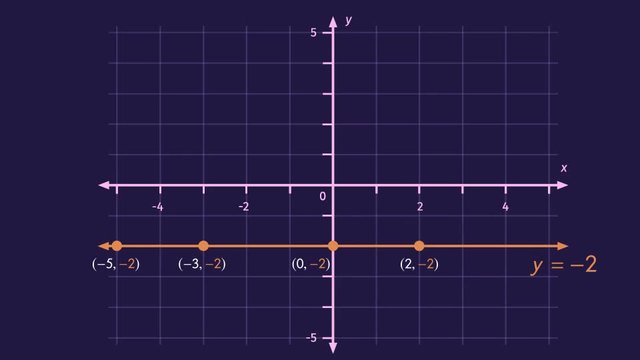
Let’s examine the horizontal line Stephanie wants 8bitbot to move along.
By examining a few points along this horizontal line, we can write an equation to describe it.
Let's pick some random ordered pairs: negative 5, negative 2; negative 3, negative 2; zero, negative 2; and 2, negative 2.
Do you notice a pattern?
Though the x-values change, the y-values are all the same at negative 2.
So, the equation of this horizontal line is 'y' equals negative two.
What other qualities does this horizontal line have?
The line is parallel to the x-axis.
This means it will never touch the x-axis, and therefore, has no x-intercept.
It does, however, have a y-intercept at zero, negative 2 and is perpendicular to the y-axis.
Additionally, do you notice anything about the slope of this horizontal line?
There doesn’t seem to be an incline at all.
So, let’s examine that by taking two points from the line and substituting them into the slope formula.
Remember, the formula to find slope is 'y' two minus 'y' one over 'x' two minus 'x' one.
We'll use the points negative 5, negative 2 and negative 3, negative 2, to calculate the slope.
That gives us zero divided by two.
But wait!
Remember, zero divided by anything is zero, so the slope, m, equals zero.
Stephanie understands the horizontal line and enters the rule ‘y' equals negative two into her program.
And 8bitbot is off!
But there’s another direction that he needs to move.
So, let's investigate this vertical line of the ladder.
Like we did with the horizontal line, we can pick and label some random points on the line.
Do you see a pattern in these ordered pairs?
Similar to the horizontal line where the y-values didn't change, we can see that the x-values don't change when the line is vertical.
Therefore, we can write the equation as 'x' equals five.
What other qualities does this vertical line have?
This vertical line is parallel to the y-axis which is another vertical line, so it won't have a y-intercept.
However, it has an x-intercept at the point five, zero and is perpendicular to the x-axis which is a horizontal line.
The vertical line is also perpendicular to our horizontal line from the first example.
So, what does that mean for the slope of the vertical line, or actually all vertical lines?
Let's examine this slope algebraically by again using the slope formula and any two points from the line.
This results in negative one over zero.
Whoa!!!! Wait a minute!
We can’t divide something by nothing.
Therefore, this slope is undefined.
In fact, all vertical lines have an undefined slope because there is no difference in the x-values.
Phew. That's good to know.
Stephanie types in 'x' equals 5 to make 8bitbot move vertically.
Look at him go!
Before Stephanie finishes her programming, let's review.
Our first example was a horizontal line with the equation 'y' equals negative two.
Let's look at a few more horizontal lines.
All horizontal lines can be written as 'y' equals some constant.
There is no 'x' term in horizontal lines because the slope is always zero.
The slope of any horizontal line is always zero, because the numerator is zero because there is no change in the y-values.
Our vertical line's equation was written as 'x' equals 5.
This is the opposite when compared to horizontal lines, as all vertical lines can be written as 'x' equals some constant.
Vertical lines have no 'y' term in the equation.
No matter what vertical line you have, the slope will always be undefined because there is a zero in the denominator.
This means there is no difference because there is no change in the x-values.
Understanding the characteristics of horizontal and vertical lines has helped Stephanie program the correct code for 8bitbot's movements.
So, what’s 8bitbot doing now?
Oh, poor Stephanie.
It must be late.
The Graphs of Horizontal and Vertical Lines exercise
-
Identify the characteristics of horizontal lines.
HintsKeep the slope tree in mind. It helps you to remember the slope of different lines.
In general a linear equation is given by $y=mx+b$, where $m$ is the slope and $b$ the $y$-intercept.
SolutionHere you see the slope tree. The part of the tree which is parallel to the bottom of the tree has a slope of zero.
Any linear equation like $y=c$, where $c$ is constant, is parallel to the bottom of the tree and thus has a slope of zero. So, the horizontal line corresponding to $y=3$, is parallel to the bottom of the tree, or the $x$-axis, and thus has a slope of zero.
Let us check this using the slope formula for two given points on the line, for example $(1,3)$ and $(4,3)$. You subtract the $y$-coordinates and divide the resulting difference by the difference of the $x$-coordinates in the appropriate order:
$m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-3}{4-1}=\frac03=0$.
This line has some further properties:
- The $y$-intercept is $(0,3)$. The line has no $x$-intercept.
- The $x$-values change while the $y$-values stay constant ($y=3$).
- The line is perpendicular to the $y$-axis.
-
Describe vertical lines.
HintsKeep the slope formula in mind: $m=\frac{y_2-y_1}{x_2-x_1}$, and remember that you can't divide by zero!
Find the part of the slope tree which represents a vertical line.
SolutionHere you see the slope tree. A line parallel to the trunk of the tree has an undefined slope. Any linear equation like $x=c$, where $c$ is constant, is parallel to the trunk of the tree and thus has an undefined slope. The horizontal line $x=2$ in particular is parallel to the trunk and thus has an undefined slope.
This line has some further properties:
- The $x$-intercept is $(2,0)$. The line has no $y$-intercept.
- The $x$-values stay constant ($x=2$) while the $y$-values change.
- The line is parallel to the $y$-axis.
$m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-0}{2-2}=\frac30$.
We cannot divide by zero because, if we could, then we could multiply both sides of the equation $m=\frac{3}{0}$ by zero to get that $0m=3$, which is not true! As any number times zero is zero. So our slope is undefined.
-
Identify the corresponding equation to the graphed line.
HintsThe equation for any horizontal line, or line parallel to the $x$-axis, is given by $y=c$, where $c$ is a constant.
The equation of any vertical line, or line parallel to the $y$-axis, is given by $x=c$, where $c$ is a constant.
SolutionRemember:
- A horizontal line (i.e. parallel to the $x$-axis) has the equation $y=c$, where $c$ is a constant.
- A vertical line (i.e. parallel to the $y$-axis) has the equation $x=c$, where $c$ is a constant.
- The red one intersects the $y$-axis at $y=2$. This is already the desired equation.
- The orange one intersects the $y$-axis at $y=1$.
- The green one intersects the $y$-axis at $y=4$.
- The violet one intersects the $x$-axis at $x=3$. That's the desired equation.
- The blue one intersects the $x$-axis at $x=1$.
-
Decide if the line is horizontal or vertical.
HintsIn general, a linear equation is given by $y=mx+b$, where $m$ is the slope and $b$ the $y$-intercept.
For any slope $m\neq 0$ the line is neither horizontal or vertical.
Determine the $y$- or $x$-intercept.
A horizontal (vertical) line has no $x$- ($y$-) intercept.
- $y=-2$ is a horizontal line.
- $x=-2$ is a vertical line.
- $y=-2x-2$ is a line which is neither horizontal or vertical.
SolutionKeep the following in mind:
- The equation of any horizontal line is given by $y=c$, where $c$ is a constant.
- The equation of any vertical line is given by $x=c$, where $c$ is a constant.
- $y=0$
- $y=7$
- $x=-2$
- $x=7$
- $y=x+1$
- $y=7x+7$
-
Identify the type of line and their corresponding equations.
HintsHere you see the line given by $y=\frac32x$.
You can see that the line is neither horizontal or vertical.
A horizontal line is parallel to the $x$-axis.
A vertical line is parallel to the $y$-axis.
The equation of any horizontal line is given by $y=c$ with a constant $c$.
The equation of any vertical line is given by $x=c$ with a constant $c$.
SolutionIn the picture you see three lines:
- The line corresponding to $y=1$ is parallel to the $x$-axis. This line is horizontal.
- The line corresponding to $x=4$ is parallel to the $y$-axis. This line is vertical.
- The last line according to $y=-x+2$ passes the $y$-axis in $(0,2)$ and the $x$-axis in $(2,0)$. This line is neither horizontal or vertical.
-
Calculate the slope of the line given two points and identify what type of line it is.
HintsUse the slope formula for two given points $(x_1,y_1)$ and $(x_2,y_2)$:
$m=\frac{y_2-y_1}{x_2-x_1}$.
Pay attention to the consistent order of subtraction.
The slope tree represents a vertical line.
In general a linear equation is given by $y=mx+b$, where $m$ is the slope and $b$ the $y$-intercept.
- A slope $m=0$ indicates a horizontal line.
- A slope $m\neq 0$ indicates a line which is neither horizontal or vertical.
- An undefined slope indicates a vertical line.
SolutionTo determine if a line corresponding to given set of points on a line is horizontal, vertical, or neither, we determine the slope of the line which the set of points defines. For this we use the slope formula:
$m=\frac{y_2-y_1}{x_2-x_1}$.
If the denominator is equal to zero the slope is undefined.
For $\mathbf{(3,3)}$ and $\mathbf{(4,3)}$, we have that
$m=\frac{3-3}{4-3}=\frac01=0$.
So we can conclude that the corresponding line is horizontal.
For $\mathbf{(3,3)}$ and $\mathbf{(3,4)}$, we have that
$m=\frac{4-3}{3-3}=\frac10$.
Division by zero is not defined, so the slope is undefined and the corresponding line must be vertical.
For $\mathbf{(3,3)}$ and $\mathbf{(4,4)}$, we have
$m=\frac{4-3}{4-3}=\frac11=1$.
This time we get a non-zero slope. Thus the line is neither horizontal or vertical.
With $\mathbf{(0,0)}$ and $\mathbf{(1,3)}$, we get the slope,
$m=\frac{3-0}{1-0}=\frac31=3$.
Once again we get a non-zero slope and thus also a line which is neither horizontal or vertical.