Constant Rate of Change

Basics on the topic Constant Rate of Change
When something has a constant rate of change, one quantity changes in relation to the other by a constant factor. One concrete example of this is the relation of distance rate and time. Learn how to use and work with constant rate of change by helping Giovanni, an Italian poet, figure out the time of arrival of the carrier pigeon to his paramour’s kingdom upon sending his love letter. Common Core Reference: CCSS.MATH.CONTENT.HSS.ID.C.7
Transcript Constant Rate of Change
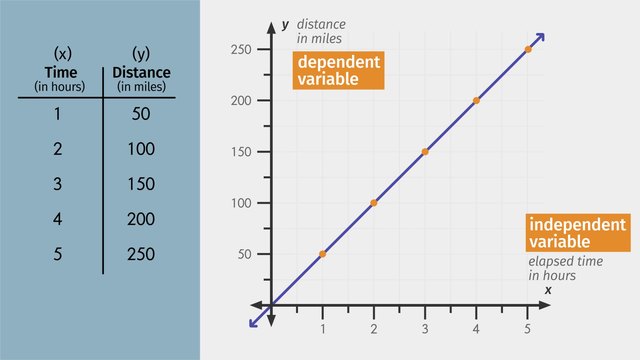
Giovanni, an Italian poet and a very old-school kind of guy, wants to send a letter to his sweetheart. The only problem is his swain lives in the neighboring kingdom, 250 miles away. He visits the local carrier pigeon salesman and purchases the fastest pigeon in all the land. Giovanni's quite impatient and wants to know when the pigeon will reach his paramour. To figure this out, and play Medieval matchmaker for Giovanni, we can use constant rate of change. When something has a constant rate of change, one quantity changes in relation to the other. For example, for every half hour the pigeon flies, he can cover a distance of 25 miles. We can write this constant rate as a ratio. For ratios, it's always a good idea to state both units in whole terms. Since we don't want to change the ratio, we multiply the ratio by its multiplicative identity property. In this case, that means multiplying both the numerator and denominator by 2 to get a whole number in the denominator. And, just like with fractions, you should always write ratios in lowest terms. Simplified, the constant rate is 50 miles per hour. Let's help Giovanni figure out where his pigeon will be after a certain amount of time has passed. We can create a table using different values for time to see how much progress the pigeon has made. We know the pigeon flies at a rate of 50 miles per hour, so after one hour, the pigeon will have flown a total of 50 miles. To find out how far the pigeon will have flown after 2 hours, we just have to multiply the rate by 2. If the pigeon flies for 3 hours, we can simply multiply our original rate by 3 to find out that the pigeon will have traveled 150 miles. We can continue this process, filling in our table as we go. Okay. Looking good. But, to get an even better understanding, let's graph the data from the table. Let the x-axis represent the elapsed time in hours, and let the y-axis represent the distance in miles. Each 'x-y', pair represents a location on the graph. Just like 'x' is an independent variable, the number of hours is the independent variable in this example. So, the total distance, 'y', is the dependent variable. Now plot the points from the table onto the graph using the ordered pair (hours and miles). Notice how the graph is a perfectly straight line! Notice that, for every hour, the pigeon flies an additional 50 miles. We can also solve this problem algebraically. Let's go back to the equation we set up earlier. We found out earlier that the rate the pigeon flies is 50 miles per hour. Substituting this back into our equation, we have rate times 2 hours equals 100 miles. Since an hour is a unit of time, we can substitute the '2 hours' in the equation with 'time'. And finally, 100 miles is the distance the pigeon flew, so we can substitute '100 miles' with 'distance'. Mathematicians typically write equations with single variables instead of words. So, to make it shorter to write, let's just use the first letters of each word. Since distance, or 'd', is our dependent variable, it's customary to write it on the left side of the equation. There, that's better. Now, we can solve any constant rate problem if we know just two of these variables. Let's plug in what we know and find out where that plumy pigeon is. He needs to fly a distance of 250 miles at a constant rate of 50 miles per hour. Now, multiplying by the reciprocal of our rate to isolate the 't' and solve Giovanni's little problem, it'll take the pigeon 5 hours to deliver the letter. Giovanni waits and waits for a response from his sweetheart. I guess he’ll just have to wait a little while longer.
Constant Rate of Change exercise
-
Explain how to get the equation representing a constant rate of change.
HintsRemember, an independent variable is something you can control, while a dependent variable is determined by the independent variable.
Rate multiplied by time equals distance.
SolutionThe equation that relates the distance the carrier pigeon has flown, to the time it has flown and its constant rate of change, can be written multiply ways.
However, since the purpose of this equation is to find the distance given a particular length of time, this equation should be written as distance equals rate times time, or, algebraically speaking, $d=50t$.
Since the distance the pigeon has flown is dependent on the amount of time it has be flying, time is the independent variable, while distance is the dependent variable.
-
Fill in the table using the given constant rate of change equation.
HintsConstruct an equation that gives the distance flown given a certain number of hours.
Multiply the time by the rate to get the distance.
SolutionTo fill in the missing values in the table, it is necessary to construct an equation relating time, rate, and distance.
Remember, multiplying the time (in hours) by the rate (in miles per hour) produces the distance the pigeon has flown (in miles). Therefore:
- $1~\text{hour}\cdot \frac{35~\text{miles}}{1~\text{hour}}=35~\text{miles}$.
- $2~\text{hours}\cdot \frac{35~\text{miles}}{1~\text{hour}}=70~\text{miles}$.
- $3~\text{hours}\cdot \frac{35~\text{miles}}{1~\text{hour}}=105~\text{miles}$.
- $4~\text{hours}\cdot \frac{35~\text{miles}}{1~\text{hour}}=140~\text{miles}$.
- $5~\text{hours}\cdot \frac{35~\text{miles}}{1~\text{hour}}=175~\text{miles}$.
-
Determine what the distance traveled is given a certain number of hours.
HintsRecall that you multiply rate and time to get distance traveled.
Rewrite the rate in miles per hour.
Rewrite $20$ minutes as a fraction of an hour to help rewrite the rate using whole terms.
SolutionAlthough the rate ratio is given in whole terms ($4$ miles in $20$ minutes), since most of the times are given in hours, it would be helpful to write the ratio in miles per hour.
$20$ minutes can be rewritten as $\frac{1}{3}$ hour. Now, you can multiply both the numerator and denominator of the ratio $4$ miles per $\frac{1}{3}$ by $3$, resulting in a rate ratio of $12$ miles per $1$ hour.
Now, you can substitute this constant rate of change in the formula $d=r\cdot t$, resulting in $d=12\cdot t$. To match each time to its corresponding distance traveled, you just need to multiply the time (in hours) by $12$.
Notice that it is necessary to convert $45$ minutes to $\frac{3}{4}$ hour so that the units reduce properly.
-
Use a table to plot points on a graph.
HintsPlot each ordered pair by starting at the point $(0, 0)$.
Use the $x$-coordinate to count that many units to the right. Then, use the $y$-coordinate to count up that many units.
When connecting the points, you should end up with a straight line.
SolutionPlotting coordinate points involve both a horizontal and vertical component.
Every coordinate point is an ordered pair of the form $(x,y)$. The $x$-value controls horizontal movement. If $x$ is positive, you move $x$ units to the right. If $x$ is negative, you move $x$ units to the left. Similarly, the $y$-value controls vertical movement. A positive $y$-value means you move $y$ units up, while a negative $y$-value means you move $y$ units down.
When plotting ordered pairs, always start at the origin, or the point $(0,0)$. Then, use the $x$ and $y$ values to plot each point accordingly.
In this graph, the points $(2,3)$, $(4,6)$, $(6,9)$, $(8,12)$, and $(10,15)$ make a straight line starting from the origin and sloping upward.
-
Identify the steps for finding the equation representing a constant rate of change.
HintsIt is important to write a formula before substituting values in for variables.
Recall that the distance formula is $d=r t$.
SolutionWhile there is more than one way to write the equation relating constant rate of change, time, and distance.
If the goal is to determine the distance given the rate and time, however, it is necessary to use the steps below:
- First, you need to make sure that your rate of change is expressed in whole terms. This means that the numerator and denominator of your ratio should be whole numbers, rather than fractions.
- Next, you need to write an equation that properly relates the three variables. Recall that distance equals rate times time.
- Then, since you've already determined the constant rate of change in whole terms, you can substitute this value into your formula.
- Lastly, in order to determine the distance that is flown over a certain number of hours, multiply the constant rate of change by the given time.
-
Determine the rate of change from the table.
HintsUse the ordered pairs from the table to determine the constant rate of change.
Think about what value of $r$ would make the equation $d = r t$ true.
Manipulating the formula distance equals rate times time, the constant rate of change equals distance divided by time.
SolutionTo determine the constant rate of change from a table, it helps to look at each set of ordered pairs and determine the relationship between the two numbers.
Recall the formula, $d = r t$.
The table gives you $5$ lengths of time with their corresponding distances. You can select any ordered pair and substitute these values into the formula.
For example: $48= r \cdot 4$ or $144= r \cdot 12$.
Now, you can think about what value of $r$ would make both of these equations true.
Since $4$ goes into $48$ twelve times, the fox should travel $r=12$ meters per second.
You can check to see if this constant rate of change works for all ordered pairs. Does $r= 12$ make the equation, $144= r \cdot 12$ true?
$12 \times 12 = 144$ ✓
Therefore, the fox can run at a constant speed of $12$ meters per second-- not quite fast enough to catch that silly rabbit.