Linear Equations in Two Variables

Basics on the topic Linear Equations in Two Variables
When a linear equation has two coefficients it is called a linear equation with two variables. Using a table or graph is useful when working with a linear equation with two variables, as they may help you understand the relationship between the two variables better. Learn how to set-up linear equations in two variables by helping Francis and Claire figure out the number of boxes of cookies they’ll need to sell in order to beat Zoe’s record last year in the “Cookie Craze Annual Fund Raiser”. Common Core Reference: CCSS.MATH.CONTENT.HSA.CED.A.2
Transcript Linear Equations in Two Variables
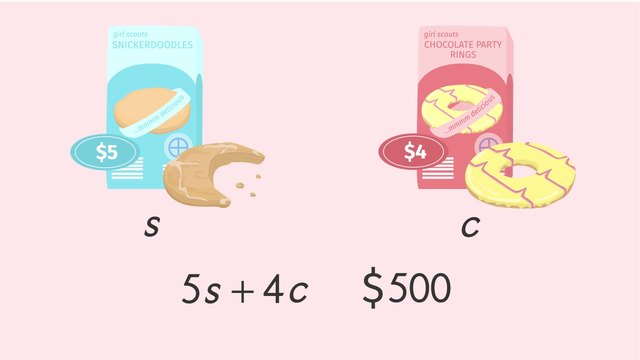
Meet Francis and Claire. The two girls are meeting at Claire’s house to get ready for the Cookie Craze annual fundraiser. Their friend, Zoe, set the fundraiser record last year for cookie sales. But this year, they're both gunning for Zoe's record. To figure out how many cookies they’ll need to sell, they’ll need to use Linear Equations with Two Variables. The girls have two different kinds of cookies they can sell: Snickerdoodles and Chocolate Party Rings. Boxes of Snickerdoodles are sold for $5 each and Chocolate Party Rings are sold for $4. Let’s help Francis and Claire set up a linear equation to help them figure out how many boxes of cookies they’ll need to sell to beat Zoe's record. Since we have two different kinds of cookies, we need two variables to represent how many boxes of each type of cookie is sold. We’ll use ‘s’ to represent the number of boxes of Snickerdoodles and ‘c’ to represent the number of boxes of Chocolate Party Rings. First, we need to have an expression for how much money the girls will make just from selling Snickerdoodles. Since Snickerdoodles cost $5 each, and the number of boxes sold is ‘s’, we can say that the total amount of money just from selling Snickerdoodles is 5s. Next, we need to have an expression for how much money the girls will make just from selling Chocolate Party Rings. Using the same logic, the girls can earn 4c dollars just from selling Chocolate Party Rings. Since Zoe's sales record is $500, we can write a linear equation by adding 5s and 4c and setting it equal to $500. This is great! But what does this tell us? Let’s take a look at a table to help us determine how many boxes of each kind of cookie the girls will have to sell in order to reach their fundraising goals. In our linear equation, 5s plus 4c equals $500. So, if we want to know how many boxes of Snickerdoodles and zero boxes of Party Rings equals $500, we should set ‘c’ equal to 0 and solve for ‘s’. Dividing both sides of the equation by 5, we find that the girls would need to sell 100 boxes of Snickerdoodles in order to make $500. Similarly, if the girls only sold boxes of Chocolate Party Rings, how many boxes will the girls need to sell in order to make the same $500? To find this out, we should substitute zero in for 's' and solve for 'c'. This time, dividing both sides of the equation by 4, we find that the girls would need to sell 125 boxes of Chocolate Party Rings in order to make $500. But what if they sold the boxes of cookies in combination? We can use our linear equation and plug in values for 's' to find out how many boxes of Chocolate Party Rings the girls would need to sell in order to make $500. Since Snickerdoodles are ordered in groups of 20 boxes, we can substitute 20 for 's' and solve for 'c'. Five times twenty is 100. Then, subtracting 100 from both sides of the equation leaves us with 4c equals 400. Finally, just like before, we divide both sides of the equation by 4 and we get 'c' equals 100. So, for 20 boxes of Snickerdoodle sales, the girls’ll need to sell 100 boxes of Chocolate Party Rings. We can repeat the process for 40 boxes of Snickerdoodles. 5 times 40 is 200. Then opposite operations, divide both sides by 4, aaand the girls’ll need to sell 75 boxes of Chocolate Party Rings. Try to fill in the rest of the chart for yourself! Did you get the same answers as us? Let’s graph these points so that we can see the relationship better. First, we can plot the points we have, starting with our intercepts, or, when one of the two values is 0. Next, let's plot our Snickerdoodle values on the x-axis and the Chocolate Party Ring values on the y-axis and finally, to connect the lines. MUCH better! Wow! It's so easy to tell how many boxes of cookies need to be sold! With a graph, we can see that if we sold 32 boxes of Snickerdoodles, we'd have to sell 85 Chocolate Party Rings. We could also sell 64 boxes of Snickerdoodles and 45 Chocolate Party Rings. That's not even on our chart! I think you'll agree, that was a lot! When you have equations with more than one variable, it’s sometimes a good idea to make a table or graph the points...or both! This could help you understand the relationship between the two variables better. Let’s see how Francis and Claire’s preparations are going. Both girls have chosen a strategy and are ready to sell some cookies!!! Huh? Zoe!?!? Uh-oh...looks like the girls have their work cut out for them if they wanna catch Zoe this year!
Linear Equations in Two Variables exercise
-
Solve the linear equation.
HintsThe keyword each indicates multiplication.
If you know the value of one of the variables, you can plug it into the equation and solve for the remaining variable.
Solve equations using opposite operations. Just have a look at the example beside.
SolutionWhat do we know?
Francis and Claire get $\$~5$ for each box of Snickerdoodles they sell and $\$~4$ for each box of Chocolate Party Rings they sell.
- First, we assign $s$ to the unknown number of Snickerdoodle boxes sold. The price $\$~5$ each indicates multiplication: so $5s$ is the total amount of money made from selling Snickerdoodles.
- In the same way, we assign $c$ to the unknown number of Chocolate Party Rings sold to get $4s$ as the total amount of money made from selling Chocolate Party Rings.
- We add these amounts together, $5s+4c$, to get the total amount of money made from selling Snickerdoodles and Chocolate Party Rings.
- Because Francis and Claire want to make $\$~500$ in total, we can establish the linear equation with two variables $5s+4c=500$.
$\mathbf{c=0}$
- Plugging $c=0$ into the equation gives us $5s=500$.
- Dividing both sides by $5$ to isolate $s$ gives us $s=\frac{500}5=100$.
$\mathbf{s=0}$
- Plugging $s=0$ into the equation gives us $4c=500$.
- Dividing both sides by $4$ to isolate $c$ gives us $c=\frac{500}4=125$.
-
Complete the Table.
HintsYou have to solve the equation $5s+4c=600$ for each given value: Just look at the example beside for $s=100$.
You see you first have to plug in the given value and than use opposite operations to isolate the unknown value.
SolutionLet's start with the solving of the equation for $c=0$:
$\begin{array}{rcl} 5s+4(0) & = & ~600\\ 5s+0&=&~600\\ 5s&=&~600\\ \color{#669900}{\div5} & & \color{#669900}{\div5}\\ s & = & ~120 \end{array}$
So, you have to proceed as follows:
- Plug the given value in the equation.
- Solve the equation using opposite operations as in the case of $c=0$ above.
$\begin{array}{rcl} 5(80)+4c & = & ~600\\ 400+4c&=&~600\\ \color{#669900}{-400} & &\color{#669900}{-400}\\ 4c & = & ~200\\ \color{#669900}{\div4} & & \color{#669900}{\div4}\\ c & = & ~50 \end{array}$
Similarly you get
- $s=60$ for given $c=75$
- $c=100$ for given $s=40$
- $s=20$ for given $c=125$
-
Identify the solutions to the linear equations with two variables.
HintsPlug in the given value into the equation and solve for the remaining variable using opposite operations.
Check your solution by plugging in both the value you solved for as well as the given value into the equation.
SolutionWe solve the unknown in each equation by plugging in the given value:
$\mathbf{3s+2c=600}$ given that $s=100$:
- $3(100)+2c=600$ or $300+2c=600$.
- Subtracting $300$ from both sides leads to $2c=300$.
- Lastly we divide both sides by $2$ to get $c=150$.
- $5s+3(100)=1200$ or $5s+300=1200$.
- Subtracting $300$ from both sides leads to $5s=900$.
- We still have to divide both sides by $5$ to get $s=180$.
- $4(15)+6c=240$ or $60+6c=240$.
- Subtracting $60$ from both sides leads to $6c=180$.
- Almost done: divide both sides by $6$ to get $c=30$.
- $4s+10(20)=400$ or $4s+200=400$.
- Subtracting $200$ from both sides leads to $4s=200$.
- We still have to divide both sides by $4$ to get $s=50$.
-
Determine the corresponding value which makes $3t+6p=750$ true.
HintsFor each $t$, there is precisely one $p$ and vice versa.
You can plug a value into the equation from the top or bottom row of values and solve for the missing variable.
Solving the equation above for $t$ leads to the linear equation $t=-2p+250$.
SolutionNow to solve the equation for each given value, we transform it once for isolating $t$ and another time isolating $p$.
Let's start by solving for $t$:
$\begin{array}{rcl} 3t+6p & = & ~750\\ \color{#669900}{-6p} & &\color{#669900}{-6p}\\ 3t & = & ~-6p+750\\ \color{#669900}{\div3} & & \color{#669900}{\div3}\\ t & = & ~-2p+250 \end{array}$
Now we are in the position to plug in the given values for $p$:
- $p=50$ leads to $t=-2(50)+250=-100+250=150$.
- $p=75$ leads to $t=-2(75)+250=-150+250=100$.
- $p=125$ leads to $t=-2(125)+250=-250+250=0$.
$\begin{array}{rcl} 3t+6p & = & ~750\\ \color{#669900}{-3t} & &\color{#669900}{-3t}\\ 6p & = & ~-3t+750\\ \color{#669900}{\div6} & & \color{#669900}{\div6}\\ p & = & ~-0.5t+125 \end{array}$
We can now plug the given values for $t$ in:
- $t=50$ leads to $-0.5(50)+125=-25+125=100$.
- $t=150$ leads to $-0.5(150)+125=-75+125=50$.
- $t=200$ leads to $-0.5(200)+125=-100+125=25$.
-
Find $c$ when $s=60$ and when $s=80$.
HintsThe opposite operation of addition is subtraction:
$\begin{array}{rcl} x+8 & = & ~30\\ \color{#669900}{-8} & &\color{#669900}{-8}\\ x & = & ~22 \end{array}$
The opposite operation of multiplication is division:
$\begin{array}{rcl} 8x& = & ~32\\ \color{#669900}{\div8} & &\color{#669900}{\div8}\\ x & = & ~4 \end{array}$
You can check your solution by plugging the value you get for $c$ as well as the value you are give for $s$ into the equation, and see if you get $500$.
For example, for $s=40$ and $c=75$:
$5(40)+4(75)=200+300=500$ $~~~~~$✓
SolutionTo solve the equation for $c$ with the given $s$ values, just plug each given value into the equation and isolate the variable $c$ using opposite operations:
$\mathbf{s=60}$
$\begin{array}{rcl} 5(60)+4c&=&~500\\ 300+4c&=&~500\\ \color{#669900}{-300} & &\color{#669900}{-300}\\ 4c & = & ~200\\ \color{#669900}{\div4} & & \color{#669900}{\div4}\\ c & = & ~50 \end{array}$
$\mathbf{s=80}$
$\begin{array}{rcl} 5(80)+4c&=&~500\\ 400+4c&=&~500\\ \color{#669900}{-400} & &\color{#669900}{-400}\\ 4c & = & ~100\\ \color{#669900}{\div4} & & \color{#669900}{\div4}\\ c & = & ~25 \end{array}$
-
Sort the solutions to the linear equations with two variables.
HintsPlug each given value into the corresponding equation and use opposite operations.
The smallest solution is $40$ and the largest one is $300$.
SolutionPlug in the given value and use opposite operations to solve for the desired solution.
- $\mathbf{2u+v=240}$ with known $u=100$ leads to $200+v=240$. Subtracting $200$ from both sides results in $v=40$.
- Plug $v=100$ into the equation $\mathbf{4u+4v=600}$ to get $4u+400=600$. Next subtract $400$ from both sides to get $4u=200$ and finally divide both sides by $4$ to get $u=50$.
- For $\mathbf{4u+6v=1200}$, plug $u=180$ in. So we get $720+6v=1200$ and subtract $720$ from both sides to get $6v=480$. Lastly divide both sides by $6$ and we get that $v=80$.
- For $\mathbf{4v+5u=1200}$, we know that $u=120$. Plugging into this value leads to $4v+600=1200$. Next subtract $600$ from both sides to gain $4v=600$ and divide by $4$ to get $v=150$.
- The next equation is $\mathbf{3u+2v=700}$ with $u=100$. Plugging this value in gives us $300+2v=700$. Subtracting $300$ from both sides leads to $2v=400$ and dividing both sides by $2$ results in $v=200$.
- Just one more equation: $\mathbf{2u+3v=1200}$ with given $v=200$. Once again we plug the given value into $2u+600=1200$ and subtract $600$ from both sides to get $2u=600$. Finally, dividing both sides by $2$ leads to the solution $u=300$.