The Graph of a Linear Equation in Two Variables

Basics on the topic The Graph of a Linear Equation in Two Variables
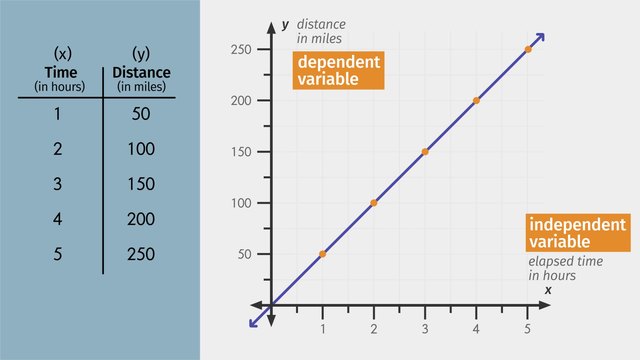
The graph of a linear equation in two variables is a straight line. This can be used to describe many relationships and processes in the physical world. It gives a visual representation of the relationship between two variables such as how quickly a projectile is moving or how fast a chemical reaction is proceeding. It can also be used to show the comparison between two units of measurement like centimeters and inches, meters and miles or degrees Celsius and degrees Fahrenheit. Learn how to graph a linear equation in two variables by helping Mei Long build a temple on top of a high hill in a village called Nanjie in order to house an enormous mythical dragon believed to bring prosperity and good fortune. Common Core Reference: CCSS.MATH.CONTENT.8.FA.3
Transcript The Graph of a Linear Equation in Two Variables
In the hilly region surrounding the village of Nanjie, a mythical dragon appears on the horizon, promising to bring prosperity and good fortune to the land. But the tiny village has no temple to house the enormous dragon. And without a temple, the dragon will leave and take his luck elsewhere. So, the villagers decide to build a structure on top of a high hill. But, how can they get all their building materials up there before the dragon leaves? In the face of this crisis, an unlikely hero emerges: Mei Long, a packing assistant with a great idea. She's going to use the Graph of a Linear Equation in Two Variables to get the job done. Mei Long's plan is to use a linear equation to get the villagers to stand in a line and pass the building material from one person to the next. A linear equation is a first-degree equation, meaning the variables are raised to the first power. The graph of a linear equation is always a straight line. This linear equation has two variables, both of which are raised to the first power. We don't see the exponents, because raising a number to the first power is the same as keeping that number the same. Let’s use this equation to set up a table, by plugging in some values for 'x'. It looks like Mei Long used -3, 0, 1, 2, and 4 so we'll use those values as well. Now to solve for 'y,' just substitute the values for 'x' from the table, one by one, into the linear equation. When 'x' is equal to negative 3, we get 'y' minus negative 3 is equal to 3. Which we can rewrite as 'y' plus 3 is equal to 3. Now, use opposite operations to solve for 'y'. y' is equal to 0. Now we can add that to our chart. Let’s solve one more. When 'x' is equal to 0, we get 'y' minus 0 is equal to 3. So 'y' is equal to 3. We can fill in 3 next to 'x' equals 0 in our chart as well. If we plug in the remaining values for 'x', we can fill in the rest of the table. Do you see a pattern? With linear equations, it’s easy to predict the next set of points because they will always increase or decrease at a constant rate. That's why, when we plot the points of a linear equation, we always end up with a straight line. Now the villagers know just where to stand in order to pass the building materials up the hill. They're working smarter, not harder! But what's going on on the other side of the hill? Without the help of the Mei Long, the villagers plotted their own points using this equation. But is this a linear equation? There are two variables, both raised to the first power, but why aren't the villagers in a straight line? Let's check these two points. They don't seem right. Let's first look at where 'x' is equal to 3 and check that the villagers plotted that point correctly. Substitute 3 in for 'x' and rewrite the equation And use opposite operations to solve for 'y.' y' is equal to 3.5. Let's correct that in the table. And now for 'x' is equal to 5. As always, rewrite the equation, then use opposite operations to solve for 'y'. y' is equal to 2.5. We can correct this in our table now, too. Okay, using our corrected points, let’s get those two villagers back in line! Mei Long and the villagers really pulled together to get that temple built to the dragon’s satisfaction. And they did such a good job, it looks like there’s more luck on the way! Fortunately, you can never have too much of a good thing. Right?
The Graph of a Linear Equation in Two Variables exercise
-
Complete the table for the equation $y+\frac{1}{2}x=5$.
HintsPlug in each value for $x$ into the equation $y+\frac{1}{2}x=5$ and solve for $y$.
Plugging in $x=4$ into $y+\frac{1}{2}x=5$, we get $y+\frac{1}{2} \cdot {4}=5$, which reduces to $y+2=5$.
Subtracting $2$ from both sides gives us $y=3$.
SolutionTo complete the table using the given $x$-values, plug in each of these $x$-values in the equation beside and isolate $y$:
- $x=0$ leads to $y+\frac12(0)=5$, which simplifies to $y=5$.
- $x=3$ leads to $y+\frac12(3)=5$, which simplifies to $y+1.5=5$. Subtracting $1.5$ from both sides gives us $y=3.5$.
- $x=5$ leads to $y+\frac12(5)=5$, which simplifies to $y+2.5=5$. Here we subtract $2.5$ from both sides to get $y=2.5$.
- $x=8$ leads to $y+\frac12(8)=5$, which simplifies to $y+4=5$. Subtracting $4$ from both sides results in $y=1$.
- $x=10$ leads to $y+\frac12(10)=5,$ which simplifies to $y+5=5$. We have to subtract $5$ from both sides to get $y=0$.
-
Determine which statements about linear equations are true.
HintsWhen writing down a linear equation, such as $2y^1-3x^1=5$, the exponents of the variables do not need to be written down, as they are always $1$: $2y^1-3x^1 = 2y-3x$.
Here you see a parabola, which is the graph of a quadratic function.
SolutionA linear equation is a first-degree equation.
What does this mean? It means that all variables in a linear equation are raised to the power of $1$.
The graph of a linear equation is always a straight line.
-
Find the table which belongs to each linear equation.
HintsCheck each given $x$ by plugging it into the linear equation.
If any ordered pair $(x,y)$ from a table is not a solution to a specific equation, then that equation cannot represented by that table. That means you can move on an try another equation.
Perhaps it's easier if you rewrite each equation as we do with the following equation:
$\begin{array}{rcl} y-2x & = & ~4\\ \color{#669900}{+2x} & &\color{#669900}{2x}\\ y & = & ~2x+4 \end{array}$
SolutionLet's check each table and the corresponding equation from left to the right:
The first table
$y-2x=4$? We plug in the given $x$-values into this equation to get:
- for $x=2$, we have $y-2(2)=4$. Adding $4$ leads to $y=8$. $~~~~$✓
- for $x=3$, we get $y-2(3)=4$, and thus $y=10$. $~~~~$✓
$y-2x=4$ is the linear equation which is represented by this table.
Likewise, you get the following matches:
- The second table represents $y+\frac12x=0$.
- The third table represents $y-x=4$.
- The fourth table represents $y+2x=3$.
- The fifth table represents $y+\frac12x=3$.
-
Graph the linear equation $y-2x=2$.
HintsYou can create a table by taking the $x$-coordinate of each possible point on the graph, and plugging it into the equation to get the corresponding $y$-coordinate. If the pair $(x,y)$ matches one of the possible points, then that point lies on the desired line.
Three points belong to the given equation.
SolutionTo draw a line corresponding to a given linear equation, you proceed as follows:
- Create a table: take some values for $x$ and plug those values into the given equation. Solve this equation for $y$. You get a bunch of ordered pairs $(x,y)$, which are entries in your table.
- Highlight those points in a coordinate plane.
- Connect those points to get the line which is represented by the given equation.
-
Identify which table belongs to which graph.
HintsFor each table, every row gives you an ordered pair $(x,y)$.
There is one decreasing line; its equation is $y+x=0$.
The other equations are:
- $y-x=0$
- $y-1.5x=0$
- $y-2x=-1$
SolutionEach row of a table gives you an ordered pair $(x,y)$. We can plot these points on the coordinate plane as follows:
- Draw a line parallel to the $y$-axis that passes through the $x$-coordinate of $(x,0)$.
- Draw a line parallel to the $x$-axis that passes through the $y$-coordinate of $(0,y)$.
- The intersection of those lines is the point $(x,y)$.
We get the following lines:
- The first table belongs to the green line. The corresponding equation is given by $y-x=0$.
- The second table belongs to the blue line and its equation is $y-1.5x=0$.
- The third table belongs to the red line and is represented by the linear equation $y+x=0$.
- The fourth table belongs to the yellow line. The corresponding equation is given by $y-2x=-1$.
-
Determine which linear equation belongs to each graph.
HintsWrite each equation in the form $y=mx+b$, where $m$ is the slope and $b$ the $y$-intercept.
Check the given points by plugging them in the given equations.
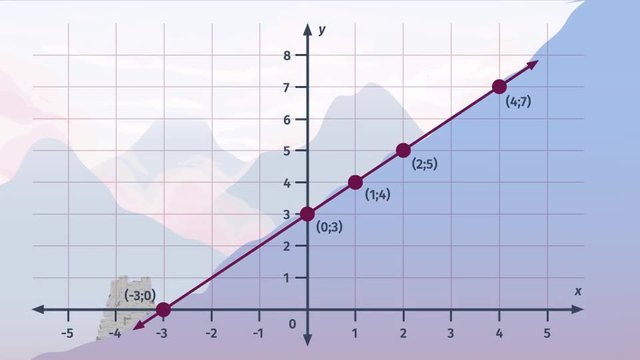
SolutionHere you see a detailed solution for the line pictured here.
You can either check the given points, $(2,2)$ and $(4,3)$, or determine the corresponding linear equation explicitly.
If you choose to determine the corresponding linear equation, then we first note that it will be of the form $y = ax + b$, where $b$ is the $y$-intercept and $a$ is the slope.
- We can see from the picture that the $y$-intercept is $b=1$.
- So we still have to determine $a$. For this, put a point on the line into the equation $y = ax + 1$ For example, $(2,2)$. You can also decide to choose the other point. The equation will be the same. You can test that yourself!
$\begin{array}{rcl} 2 & = & 2a + ~1\\ \color{#669900}{-1} & &\color{#669900}{-1}\\ 1 & = & 2a\\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ ~\frac12 & = & a \end{array}$
That's it! The desired equation is thus given by $y = \frac12x + 1$, which is the same as $ y - \frac12x = 1 $.
The equation corresponding to the leftmost graph is given by $y-2x=-1$.
The equation corresponding to the second graph from the right is given by $y+\frac12x=3.5$.
The equation corresponding to the rightmost graph is given by $y-\frac32x=-0.5$.