The Angle Sum Theorem


Basics on the topic The Angle Sum Theorem
After this lesson, you will be able to prove that the interior angles in a triangle always sum to 180˚. The lesson begins by teaching you to rearrange the angles in a triangle to form a straight angle. It leads you to learn that the angles in a triangle, just like in a straight angle, always add up to 180°. It concludes with a strategy for finding the missing angle in any triangle. Learn about the Angle Sum Theorem by helping Laura the archeologist bring the mighty Sekhmet back to life.
This video includes key concepts, notation, and vocabulary such as congruent, parallel, transversal, and alternate interior angles. Before watching this video, you should already be familiar with properties of straight angles (they equal 180°) and alternate interior angles (they are congruent). After watching this video, you will be prepared to learn how to find the missing angles in any triangle, including exterior angles. Common Core Standard(s) in focus: 8.G.A.5 A video intended for math students in the 8th grade Recommended for students who are 13-14 years old
Transcript The Angle Sum Theorem
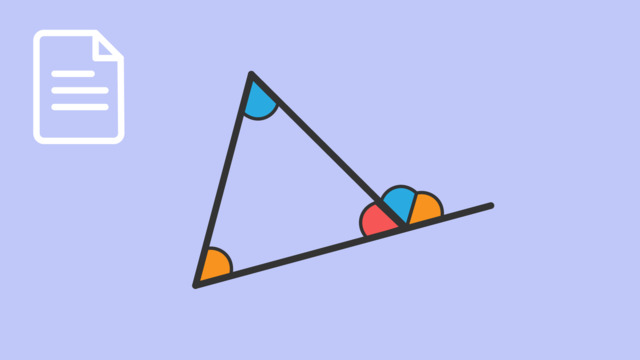
Many moons ago, the Egyptian goddess Sekhmet was entombed in the ancient pyramids. Unfortunately, her sarcophagus is missing a few pieces! It is said that if all the missing pieces are restored, the sarcophagus will open, and the mighty Sekhmet will be reborn. We have traveled the globe to collect the missing pieces of Sekhmet's sarcophagus and have returned to the old pyramid to see if the legend holds true. Let's try to put the pieces in the right places but we'll have to get it right on the first try, or the vengeful lion goddess will trap us in the pyramids forever! We can get it right on the first try by using the angle sum theorem. We have four pieces, so let's see which one fits in this first triangle. First, we'll label the interior angles of this triangle 'a', 'b' and 'c'. We know that angle 'c' measures 92 degrees and the measure of angle 'b' equals 35 degrees. So what about the measure of angle 'a'? Let's use what we know about parallel lines, transversals, and the angles they create to solve this problem and find the missing piece. Notice that these two lines are parallel and this is the symbol for parallel. Therefore, we can call this line along the right side of our triangle a transversal because it intersects two lines. What do you remember about the angles formed by parallel lines cut by transversals? Notice that angle 'b' is an interior angle between the parallel lines. So what about this alternate interior angle? Recall that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. Therefore, this angle will also be equal to the measure of angle 'b'. But what about angle 'a'? Notice this line is a transversal that creates angle 'a' and intersects two parallel lines. Therefore, this alternate interior angle will also be equal to the measure of angle 'a'. Hmm... that's interesting. Do you notice that angles 'a', 'c', and 'b' form a straight angle because they all lie along the same line? What is the measure of a straight angle? That's right, 180 degrees. That means if we add up the measures of all three angles, 'a', 'b', and 'c', we get 180 degrees. Oh wait... that's even more interesting. The sum of the interior angles of the triangle also equals 180 degrees. But we still don't know the measure of angle 'a'. However, we do know 'b' and 'c'. So, let's use substitution and replace the measure of angle 'b' with 35 degrees and the measure of angle 'c' with 92 degrees. Using addition to simplify the left side of the equation then using the subtraction property of equality tells us that angle 'a' is 53 degrees. Let's look at the pieces we have. Which one could fit? Let's use our trusty protractor. Nice, this first one measures 53 degrees. We carefully place this missing piece because we don't want to be trapped. Phew, it fits perfectly. We have three pieces left. Let's hope they fit. We quickly measure the remaining pieces and get the following measurements. Summing the measurements of all the angles, 55 plus 110 plus 15, we notice that the interior angles of this triangle also sum to 180 degrees. What happens when we put the angles together visually? Notice that they also form a straight angle, which as we know measures 180 degrees. Let's try to put the pieces in the right places. The smallest acute angle of 15 degrees must go in this bottom left corner. The obtuse angle of 110 degrees goes in the top. The last acute angle of 55 degrees should go in the bottom right corner. But, before we place the final piece let's review the Angle Sum Theorem. The Angle Sum Theorem tells us that the sum of the measures of the interior angles of a triangle is 180 degrees. We can prove this by using properties of parallel lines cut by transversals. This creates alternate interior angles that are congruent. Because the angles that form a straight angle equal 180 degrees the angles in a triangle must also equal 180 degrees. Using the Angle Sum Theorem, we can always find the missing angle in a triangle if we know the measurements of the other two. Now let's see what happens when we place the last piece, so the mighty goddess Sekhmet can be reborn! Hmm, that's not quite what we expected.