Constructing Triangles

Pharaoh Ahmose is lounging under the bright Egyptian sun and needs a tapestry to provide some shade. So he summons his tailors. The tailors must all assemble the tapestry by each creating the same triangular piece of fabric. They'll have to construct triangles with specific angle or side measurements, as dictated by the pompous pharaoh. First, Ahmose demands a right triangle. How can we make that triangle just given one angle measurement? Let's start by using our ruler to draw a ray and labeling the point it starts from as 'C'. Remember that a ray starts at a point and goes on forever. Let's make a right angle at point 'C' by using our protractor to measure 90 degrees. Using a straight edge tool draw a ray from point 'C' through this mark, to construct a right angle.
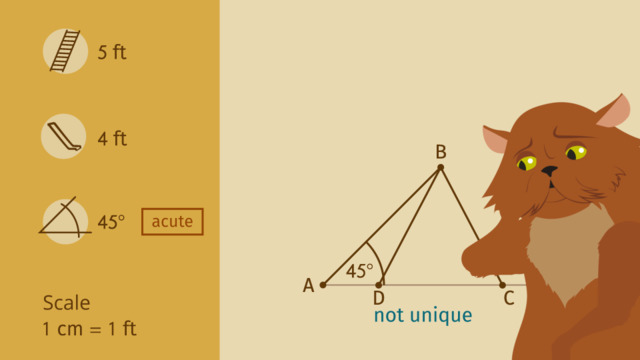
Now, let's pick one point on each ray... and then connect them with a line segment. Let's call these points 'A' and 'B'. Are we sure that triangle 'ABC' is right? Well, the measure of angle 'C' is 90 degrees, a right angle, so yes! Let's compare our right triangle with those of the tailors. Looks like the command of just giving us one angle measurement didn't give us all the same triangle. Pharaoh Ahmose wants us to create a unique triangle, that is a triangle that can only be drawn one way. How then was such variety possible? Notice that if we match up the right angle of the triangle A prime B prime C prime with ours we still have a right triangle but it is not the same. The same is true for triangle A double prime B double prime C double prime. Therefore, creating a triangle with Pharaoh Ahmose's one command to make a right triangle does not create a unique triangle. In fact, with his command we could make an infinite number of different right triangles by varying the lengths of the legs. Pharaoh Ahmose gives a new command that includes one angle and two side measurements. "All triangles must have one side length of 10 cm, another of 6 cm, and one angle of 30 degrees." Will these given measurements create a unique triangle so we just have one pattern from all the tailors? To find out let's use a ruler to start constructing a triangle with a side length of 10 cm. We'll call this segment 'E'...'F'. Now, let's use our protractor to measure 30 degrees from this segment at point 'F'. We draw a ray from 'F' to construct the 30 degree angle. Finally, let's measure 6 cm from 'F' to construct segment 'DF'. Then we connect points 'D' and 'E' with a line segment to complete the triangle. Have we obeyed Pharaoh Ahmose's command? Line segment 'EF' is 10 cm, line segment 'FD' is 6 cm, and angle 'F' is 30 degrees, so yes! But look, the tailors have created different triangles by following the same command?! The measurements given didn't provide a unique triangle. How did that happen? Look 'E' prime 'F' prime is also 10 cm. And the measure of angle 'F' prime is 30 degrees. But segment D prime F prime is not 6 cm. DF' and 'D' prime 'E' prime are the same length, but they are not corresponding and angle 'E' and angle 'E' prime are clearly different measures! There are only a few possible triangles we can make which obey the pharaoh's second command, but these triangles are different from each other. Pharaoh Ahmose really needs his tapestry to feature one, unique triangle. Therefore, Pharaoh Ahmose's third command gives three side measures. "All triangles must have side lengths of 9 cm, 7 cm, and 4 cm." Using our ruler let's draw the longest segment of 9 cm and label it 'PQ.' Next using our compass let's capture 7 cm on our ruler. Then place the needle at point 'Q' and draw an arc. Next capture 4 cm with the compass and ruler. Then place the needle on point 'P' and draw an arc to find where the two sides will meet. Let's call this point of intersection 'R.' Then use our ruler to draw sides QR and 'PR.' Viewing the tailor's triangles we see they are just reflections and rotations of our triangle! They are all congruent because they have the same size and same shape. No matter how we construct it, there can be only one triangle with side lengths 9, 7, and 4 cm in length. Therefore, Pharaoh Ahmose's command giving three side measurements provided a unique triangle! While the tailors quickly make the tapestry, let's review how we construct triangles. We often construct angles with a protractor, and side lengths with a ruler, and/or compass. Given one angle measurement allows for infinitely many triangles to be constructed. Given two sides and one angle measurement provides a few variations of triangles. And given three side measurements gives us one unqiue triangle. Ahmose is pleased with his tailors' work. But not so much by his cat.