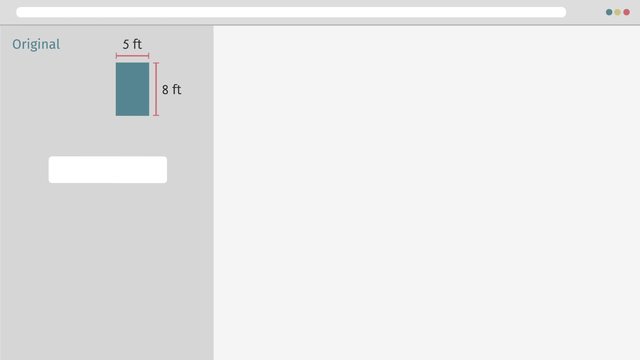
Solving Area Problems Using Scale Drawings
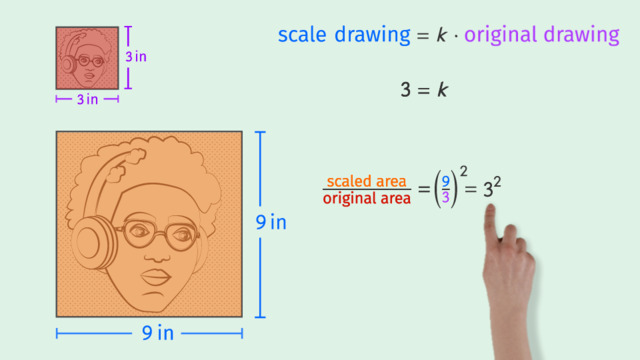

Basics on the topic Solving Area Problems Using Scale Drawings
After this lesson you will be able to solve area problems related to scale drawings.
The lesson begins by finding the scale factor or constant of proportionality, k. It leads to using the scale factor to describe the relationship between the areas of drawings. It concludes with learning that the scaled area can be found by multiplying the square of k times the original area.
Learn how to solve area problems using scale drawings by helping Malik make his very first zine!
This video includes key concepts, notation, and vocabulary such as: scale factor (the constant of proportionality, k, between two similar objects); and the formula, scaled area equals k squared times original area.
Before watching this video, you should already be familiar with area of shapes, the notation for “k squared”, and the equation Quantity = Percent x Whole.
After watching this video, you will be prepared to solve more advanced word problems involving scale factors and percents.
Common Core Standard(s) in focus: 7.RP.A.2b, 7.G.A.1
Transcript Solving Area Problems Using Scale Drawings
Malique has been collecting zines and self-published comics for a while now. He's a huge fan of the artwork, and he's got some talent for it himself! Now that he's finally decided to sit down and create his very own zine he's going to need his pencils, sketchbook, and knowledge of scale to solve area problems using scale drawings. For the first panel in his zine, Malique wants to take a self-portrait from his sketchbook and enlarge it. His original portrait is a square with side lengths of 3 inches. The scaled version will be a square with side lengths of 9 inches. How can we describe the relationship between the areas of these two drawings? Let's answer that question by first taking a look at the scale factor. Remember any length on a scale drawing is equal to the scale factor times the corresponding length on the original drawing. We can solve for 'k' with division, which gives us an equation involving a ratio you might recognize: Scaled drawing over original is equal to 'k', also known as the constant of proportionality. Substituting Malique's scaled side length and original side length into the equation we find that 'k' is equal to 3. But how can we use the scale factor to describe the relationship between the areas of these drawings? Malique's original drawing has an area of 3 inches times 3 inches. The scaled drawing's area is 9 inches times 9 inches. Before we go any further, how could this ratio be written using our scale factor? Since 9 times 9 is 9 squared and 3 times 3 is 3 squared we can reduce this fraction to see the ratio of the areas is the same as the square of the scale factor. In general, the ratio between any scaled area and it's original is equal to the scale factor squared. So the scaled area of Malique's portrait is equal to the square of the scale factor times the original area. Malique's next sketch has a circular frame with a radius of 2 inches. The final version will be an enlargement, with a radius 140 percent the size of the original. So, what will be the area of the enlarged sketch? Let's try out our formula from the last example, scaled area equals 'k' squared times the original area. What number should we use for our scale factor, 'k'? We're told that the radius of the enlarged circle is 140% or 1.4 of the original, so that's our scale factor. Now how can we use the given radius length to find the original area? As you remember, the area of a circle can be found by multiplying pi times the radius squared. So we substitute in the value of the original radius, 2 inches. Which gives us an area of 4 pi square inches. Plugging that into our formula, now we can solve for the scaled area. Malique's final circle has an area of 7.84 pi square inches. Malique has big plans for his zine's front cover. He's using a special reflective material for the background, shown here as the shaded part of his design. His original sketch is a 4 inch by 4 inch square and the final cover will be a 10 by 10 square. The reflective material covers 20 square inches on the final zine cover so how big is the shaded area on Malique's original sketch? Once again, we'll have to rely on our formula, scaled area equals 'k' squared times the original area. First, let's find the scale factor, by taking the side length 10 inches on our scaled drawing and dividing by the side length of 4 inches on the original. That reduces to 2.5 or 250%. Let's drop this value into our equation. Now, is 20 square inches our scaled area or original? We know the area of the shaded region on Malique's final cover is 20 square inches so that's the scaled area in our formula. Solving for the original shaded area in Malique's drawing we find that the original shaded area covered just 3.2 square inches. To review, scale drawings share a constant of proportionality, 'k', which describes the relationship between corresponding lengths in the scaled drawing compared to the original. The scaled area can be found by multiplying the square of 'k' times the original area. Remember, this applies to both whole areas and partial areas, as we found in Malique's cover page drawing. So the ratio of any scaled area to its corresponding original area is equal to the constant of proportionality squared. It looks like Malique is putting the finishing touches on his first ever self-published zine. Let's see how it turned out. Whoa! That's pretty high-concept, for a comic book.