Solving Absolute Value Equations


Basics on the topic Solving Absolute Value Equations
Just to refresh your memory, absolute value is the distance of a number from zero. We can also think of it as the magnitude of a number without considering the sign. The absolute value of a number is always a positive number, and the absolute value of zero is zero. You can add, subtract, multiply, and divide with the absolute value of a number. But, how do you solve for the variable of an equation when the variable is part of an expression inside absolute value bars?
The absolute value of the variable expression must be a positive number, but the value of the variable expression inside the bars can be negative or positive. So, if you are trying to determine the value of the variable inside the bars, you must set up two different equations, one positive and the other negative. The answer is one or the other, so the solution can have two different answers.
You will want to verify that both answers work by substituting them back into the corresponding equation. Be careful not to mix up the equations. We use absolute value all the time in the real world. Think about this statement, “Wow, your weight really changed!” This statement can take on two different meanings. Does the statement mean you lost weight or gained weight? It could go either way, just like the value of a variable inside absolute value bars. For more on this, watch the video.
Represent and solve equations with absolute value.
CCSS.MATH.CONTENT.HSA.REI.D.11
Transcript Solving Absolute Value Equations
Jasmine is on a plane, flying to her vacation destination. She's super excited about the trip! She bought a vacation package for an amazing price, but there may be one teeney weeney little problem with her plan… she has no idea where the plane will land. The vacation destination is a surprise.
All Jasmine knows is that there will be a 30° Fahrenheit temperature difference between her home and the vacation spot. At home, it's 60° Fahrenheit, so Jasmine imagines that soon she’ll be hanging out at a beach or exploring a jungle for lions and tigers. The airplane just landed, but wait...
Absolute value equations
Something’s not right…Looking out the window, Jasmine sees there’s no sun at all, only grey skies and lots of snow. She can’t figure out how she made such a mistake. Let's explore solving absolute value equations and figure out where Jasmine went wrong. First, we'll summarize what we know.
Summary of prior knowledge
The temperature at Jasmine's home is 60° Fahrenheit. We don’t know the temperature of the unknown vacation destination, so we'll use the variable 'x'. Jasmine is guaranteed that the temperature difference between her home and the vacation spot is 30° Fahrenheit. What she doesn’t realize is that the temperature difference could be 30° higher or 30° lower than at home.
First Example
She forgets that the absolute value of a number is always positive. Let's show her how to set up the equation to model this situation. The |x - 60| = 30. The expression inside the absolute value bars can equal 30 or -30, so to solve, we need to set up two different equations.
Now solve each equation by adding 60 to both sides of both equations, thereby isolating the variable 'x'. We're left with two possible solutions: x = 90°F......or x = 30° F. Remember, it’s always a good idea to check your work. (pause...) Poor Jasmine, she planned for a vacation in 90° weather but arrived at a destination with 30° weather! No wonder she's freezing rather than frolicking in the sun.
Second Example
Now that you get the concept, let’s solve another absolute value equation. The |4x + 20| = 100. Remember to set up two different equations, one equaling a positive value, and the other equaling a negative value. 4x + 20 = 100 and 4x + 20 = -100.. Subtract 20 from both sides of each equation, isolating the term 4x....then divide by 4 on both sides of each equation.
Positive and negative equations
For the positive equation, x = 20 and for the negative equation, x = -30. It's always a good idea to check your work to make sure both solutions work. Make sure you plug the right solution into the right equation. For the positive equation, plug in 20 for x. And for the negative equation, plug in -30 for x.
Solutions
Both solutions work, so you're good to go. The two possilble solutions for this absolute value equation are 20 or -30. You know practice makes perfect, so let’s do one more problem. The |x - 2| + 8 = 2. To solve, first isolate the absolute value before setting up the two different equations. Subtract 8 from both sides of the equation, so now the |x - 2| = -6. Negative six?
But wait, absolute value is always a positive number, never negative, so for this problem, there's no possible solution. Poor Jasmine. Standing in the snow, she’s simply shivering in her sandals. Oh look…Seems like the temperature might be warming up for Jasmine.
Solving Absolute Value Equations exercise
-
What is the temperature at the vacation resort?
HintsUse a number line to model absolute value.
Check your work. The temperature difference from $60^{\circ}$F has to be $30^{\circ}$F.
If you get stuck, refer back to the definition of absolute value:
$|x|= \begin{cases} x& \text{if }x>0 \\ -x& \text{if }x<0 \\ 0& \text{if }x=0 \end{cases}$
SolutionPoor Jasmine. She didn't know to bring warm clothes.
She assumed the temperature at her vacation spot would be $90^{\circ}$F. But what happened?
A $30^{\circ}$F temperature difference was advertised.
One possible solution: a temperature of $90^{\circ}$F because $90-30=60$.
Unfortunately, there was no guarantee of a higher temperature. The temperature could also be colder than the home temperature.
Let's solve the absolute value equation we set up earlier.
$|x-60|=30$
The definition of an absolute value equation is as follows:
$|x|= \begin{cases} x& \text{if }x>0 \\ -x& \text{if }x<0 \\ 0& \text{if }x=0 \end{cases}$
Splitting the equation above into two equations gives us:
- $x-60=30$
- $x-60=-30$
- $x=90^{\circ}$F
- $x=30^{\circ}$F
-
Solve the absolute value equation.
HintsThe definition of an absolute value is:
$|x|= \begin{cases} x& \text{if }x>0 \\ -x& \text{if }x<0 \\ 0& \text{if }x=0 \end{cases}$
Use opposite operations to solve equations.
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
SolutionLet's solve the absolute value equation: $|4x+20|=100$.
Remember the definition for absolute value:
$|x|= \begin{cases} x& \text{if }x>0 \\ -x& \text{if }x<0 \\ 0& \text{if }x=0 \end{cases}$
According to the definition above, we write two equations:
- $4x+20=100$
- $4x+20=-100$
$\begin{array}{rcll} 4x + 20 &=& -100& \\ \color{#669900}{-20} && \color{#669900}{-20} &~~~~~|~ \text{Opposite Operations} \\ 4x &=& -120 \\ \color{#669900}{\div{4}} && \color{#669900}{\div{4}} &~~~~~|~ \text{Opposite Operations} \\ x &{=}& -30 & \end{array}$
$~$
$\begin{array}{rcll} 4x + 20 &=& 100& \\ \color{#669900}{-20} && \color{#669900}{-20} &~~~~~|~ \text{Opposite Operations} \\ 4x &=& 80 \\ \color{#669900}{\div{4}} && \color{#669900}{\div{4}} &~~~~~|~ \text{Opposite Operations} \\ x &{=}& 20 & \end{array}$
We can check both solutions by plugging them into the corresponding equation:
- $|4(-30)+20|=|-120+20|=|-100|=100$ $\surd$
- $|4(20)+20|=|80+20|=|100|=100$ $\surd$
-
Deduce the resulting rates.
HintsFor example:
- The absolute value equation $|x-3|=4$ produces two equations.
- $x-3=4$ and $x-3=-4$
You can solve the equation above by adding $3$ to both sides of both equations to calculate: $x=7$ and $x=-1$.
One car is faster than the other. Check your formula!
SolutionWe know the top speed of Jasmine's old car, 75 mph. We also know that Jasmine's parents have promised a difference of 45 mph compared to her old car. We'll let $x$ be the unknown top speed of the new car. We can describe this situation by using an absolute value equation:
$|x-75|=45$
Because $|45|=|-45|$, we have to set up two equations - without the absolute value bars:
$\begin{array}{rcll} x-75 & = & 45 \\ \color{#669900}{+75} & & \color{#669900}{+75} &~~~~~|~ \text{Opposite Operations} \\ x& = & 120\\ \end{array}$
This is the faster car. Jasmine can race at a speed of 120 mph.
$\begin{array}{rcll} x-75 & = & -45 \\ \color{#669900}{+75} & & \color{#669900}{+75} &~~~~~|~ \text{Opposite Operations} \\ x& = & 30\\ \end{array}$
This is the slower car. Jasmine can putter around town at a speed of 30 mph.
-
Analyze the absolute value equations.
HintsAn absolute value equation can generate zero equations or up to two equations depending on the value of the number on the right side of the equal sign.
Look at the example $|x-7|=a$. The number of solutions depends on the value of $a$:
$|x-7|=a\text{ has } \begin{cases} \text{two solutions}& \text{if }a>0 \\ \text{one solution}& \text{if }a=0 \\ \text{no solutions}& \text{if }a<0 \end{cases}$
First rewrite each absolute equation so that you have the absolute value term on the left side of the equal sign and a constant on the right.
SolutionThe number of solutions to an absolute value equation depends on the term on the right side:
- There are two solutions if the right side is positive.
- There is one solution if the right side is equal to zero.
- There are zero solutions if the right side is negative.
$\begin{array}{rclcrcl} &&&\mathbf{|2x+3|=2}&&& \\ 2x + 3 &=& 2& &2x+3&=&-2\\ \color{#669900}{-3} && \color{#669900}{-3} &~~~|~ \text{Opposite Operations}~|~~~ &\color{#669900}{-3} && \color{#669900}{-3}\\ 2x &=& -1 & &2x &=& -5\\ \color{#669900}{\div{2}} && \color{#669900}{\div{2}} &~~~|~ \text{Opposite Operations}~|~~~&\color{#669900}{\div{2}} && \color{#669900}{\div{2}} \\ x &=& -0.5 & & x &=& -2.5 \end{array}$
Since the number on the right side of the equal sign is positive, there are two solutions.
$~$
$\begin{array}{rclcrcl} &&&\mathbf{|2x+3|+2=2}&&& \\ &&&\mathbf{|2x+3|=0}&&& \\ 2x + 3 &=& 0& &&& \\ \color{#669900}{-3} && \color{#669900}{-3} &~~~|~ \text{Opposite Operations}~|~~~ &&& \\ 2x &=& -3& &&& \\ \color{#669900}{\div{2}} && \color{#669900}{\div{2}} &~~~|~ \text{Opposite Operations}~|~~~ &&& \\ x &=& -1.5 & &&& \end{array}$
Since the absolute value is equal to zero, there is only one solution.
$~$
$\mathbf{|2x+3|+5=2}$
This equation is equivalent to $|2x+3|=-3$. Notice the number on the right side of the equal sign is negative. Since this is not possible, the equation has no solution.
$~$
$\begin{array}{rclcrcl} &&&\mathbf{-|2x+3| + 5=2}&&& \\ &&&\mathbf{-|2x+3| = -3}&&& \\ &&&\mathbf{|2x+3| = 3}&&& \\ 2x + 3 &=& 3& &2x+3&=&-3\\ \color{#669900}{-3} && \color{#669900}{-3} &~~~|~ \text{Opposite Operations}~|~~~ &\color{#669900}{-3} && \color{#669900}{-3}\\ 2x &=& 0 & &2x &=& -6\\ \color{#669900}{\div{2}} && \color{#669900}{\div{2}} &~~~|~ \text{Opposite Operations}~|~~~&\color{#669900}{\div{2}} && \color{#669900}{\div{2}} \\ x &=& 0 & & x &=& -3 \end{array}$
Since the number on the right side of the equal sign is positive, there are two solutions.
$~$
$\mathbf{-|2x+3|=2}$
This equation is equivalent to $|2x+3|=-2$. Notice the number on the right side of the equal sign is negative. Since this is not possible, the equation has no solution.
-
Explain why absolute value equations can have two solutions.
HintsRemember the definition for absolute value:
$|x|= \begin{cases} x& \text{if }x>0 \\ -x& \text{if }x<0 \\ 0& \text{if }x=0 \end{cases}$
An absolute value equation is always equal to zero or a positive number.
SolutionThis is an example of an absolute value equation. Notice the variable is located inside the absolute value bars.
- $|x-60|=30$
Therefore, absolute value equations can have as many as two solutions.
Can an absolute value equation have zero solutions? Sure! If we look at $|x-2|=-6$, we can conclude that this equation has no solution. Why? The absolute value of any number is always equal to a positive number or zero.
Therefore, it is possible to have an absolute value equation with zero solutions.
Can an absolute value equation have only one solution? This is also possible. Just look at the following example $|x-2|=0$. According to the definition of an absolute value equation, we get one equation: $x-2=0$, since zero isn't positive nor is it negative $x=2$ is the only possible solution.
-
Solve the absolute value equations.
HintsManipulate the equations to show the absolute value term only on the left side of the equal sign and the constant on the other.
Use opposite operations to manipulate the equations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
You can also check the each solution by plugging it into the absolute value equation.
SolutionTo solve absolute value equations:
- Rewrite each absolute value equation to show the absolute value term on the left side of the equal sign and the constant on the right side.
- Leave off the absolute value bars.
- Solve each equation by using opposite operations.
$\begin{array}{rclcrcl} &&&\mathbf{2|x+1|-3=5}&&& \\ &&&\mathbf{2|x+1|=8}&&& \\ &&&\mathbf{|x+1|=4}&&& \\ x + 1 &=& 4& &x+1&=&-4\\ \color{#669900}{-1} && \color{#669900}{-1} &~~~|~ \text{Opposite Operations}~|~~~ &\color{#669900}{-1} && \color{#669900}{-1}\\ x &=& 3 & &x &=& -5 \end{array}$
$~$
Equation 2: $\mathbf{-\frac12|x+4|=-2}$
$\begin{array}{rclcrcl} &&&\mathbf{-\frac12|x+4|=-2}&&& \\ &&&\mathbf{\frac12|x+4|=2}&&& \\ &&&\mathbf{|x+4|=4}&&& \\ x + 4 &=& 4& &x+4&=&-4\\ \color{#669900}{-4} && \color{#669900}{-4} &~~~|~ \text{Opposite Operations}~|~~~ &\color{#669900}{-4} && \color{#669900}{-4}\\ x &=& 0 & &x &=& -8 \end{array}$
$~$
Equation 3: $\mathbf{|2x+4|=6}$
$\begin{array}{rclcrcl} &&&\mathbf{|2x+4|=6}&&& \\ 2x + 4 &=& 6& &2x+4&=&-6\\ \color{#669900}{-4} && \color{#669900}{-4} &~~~|~ \text{Opposite Operations}~|~~~ &\color{#669900}{-4} && \color{#669900}{-4}\\ 2x &=& 2 & &2x &=& -10 \\ \color{#669900}{\div2} && \color{#669900}{\div2} &~~~|~ \text{Opposite Operations}~|~~~ &\color{#669900}{\div2} && \color{#669900}{\div2}\\ x &=& 1 & &x &=& -5 \\ \end{array}$
$~$
Equation 4: $\mathbf{4-|2x+3|=-7}$
$\begin{array}{rclcrcl} &&&\mathbf{4-|2x+3|=-7}&&& \\ &&&\mathbf{-|2x+3|=-11}&&& \\ &&&\mathbf{|2x+3|=11}&&& \\ 2x + 3 &=& 11& &2x+3&=&-11\\ \color{#669900}{-3} && \color{#669900}{-3} &~~~|~ \text{Opposite Operations}~|~~~ &\color{#669900}{-3} && \color{#669900}{-3}\\ 2x &=& 8& &2x&=&-14\\ \color{#669900}{\div2} && \color{#669900}{\div2} &~~~|~ \text{Opposite Operations}~|~~~ &\color{#669900}{\div2} && \color{#669900}{\div2}\\ x &=& 4 & &x &=& -7 \\ \end{array}$



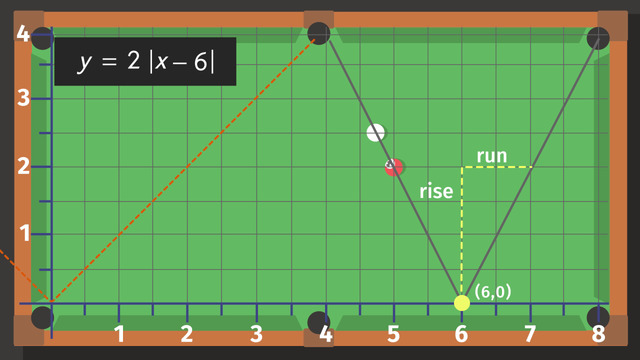











This is an absolute value equation. There are two answers.
Answer for what? Ridge?
idk ridge
whats the answer