Absolute Value

Content

• Introduction
• Absolute Value Equations
• Absolute Value Inequalities
• Absolute Value Functions

Introduction

How do we use absolute value in the real world? Absolute value is useful to calculate temperature variations, differences in height and depth, distances, as well as lots of other applications.

Absolute value, also known as modulus, can be defined as the distance of a number from zero, the magnitude of a real number without regard for sign or the numerical value of a number.

To indicate the absolute value of a number, write a number or variable between two vertical bars.

In Algebra 1, students learn how to solve, graph, and write solutions for absolute value equations, absolute value inequalities, and absolute value functions for use in the classroom and the real world.

Solutions to absolute value problems may be displayed using set or interval notation symbols. Proper notation includes curly braces { }, brackets [ ], parentheses ( ), and other symbols to provide information in a concise format $\mathbb{R}$ $\cap$.

Absolute Value Equations

Absolute value equations can have more than one solution or no solution at all.

$\begin{align} |x| & = 2 \\ x & = 2, -2 \\ x & = { -2, 2 } \end{align}$

$\begin{align} |x| & = -2 \\ x & = \text{no solution} \end{align}$

Absolute Value Inequalities

Absolute value inequalities have different formats depending if the inequality is less than; less than or equal to; greater than; or greater than or equal to. These are known as compound inequalities. The solutions to compound inequalities are written as inequalities separated by “and” for less than or less than or equal to inequalities or “or” for greater than or greater than or equal to inequalities.

$\begin{align} \left|x\right|\le 2\\ -2\leq x\leq2\\ x\geq -2 \thinspace \text{AND} \thinspace x\leq 2\\ x = [ -2, 2 ] \end{align}$

$\begin{align} \left|x\right|\ge 2 \\ x\leq -2 \quad \text{OR} \quad x\geq 2 \\ x = (-\infty \:,\:-2]\cup \:[2,\:\infty \:) \end{align}$

The graphs of absolute value inequalities have a different appearance depending if the graph models less than; less than or equal to; greater than; or greater than or equal to inequalities. The use of open or closed circles demonstrates if the end points are included in the solution.

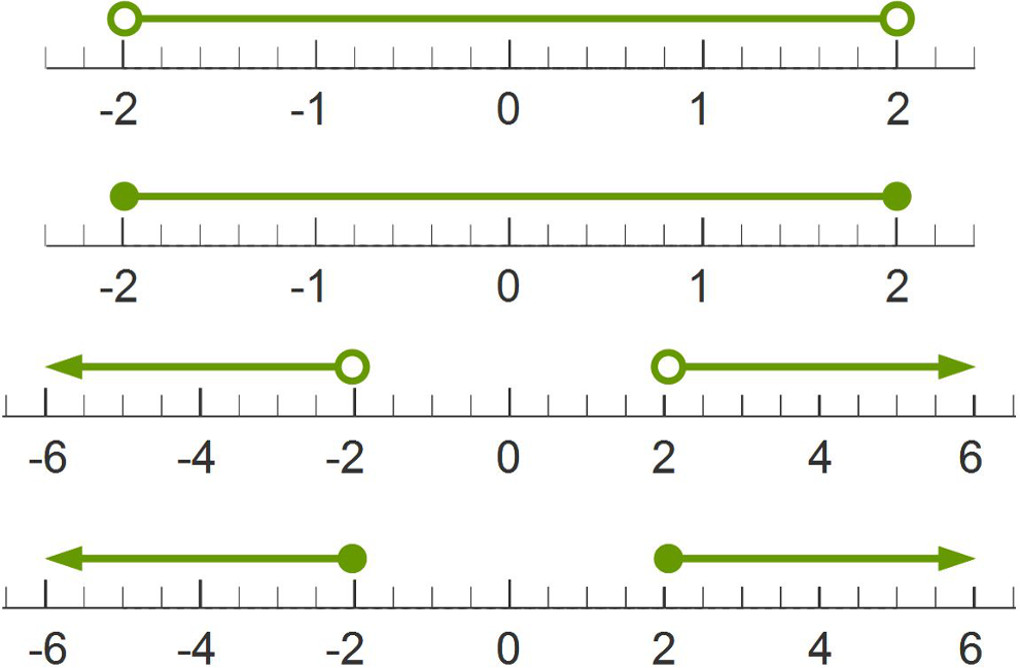
Absolute Value Functions

Absolute value functions have an input and an output, and the graph of absolute functions is in two pieces and has a V-shape. Graphs of functions having more than one piece are known as piecewise functions.

The parent function for absolute value is $|x| = y$.

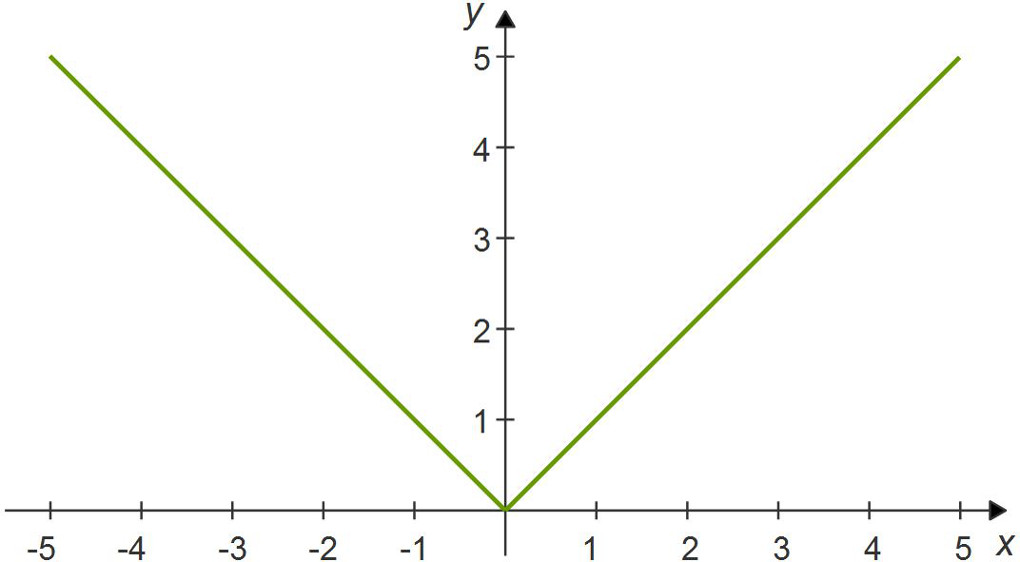
The vertex for the parent function is located at ( 0 , 0 ).

$| x +1 | = y$

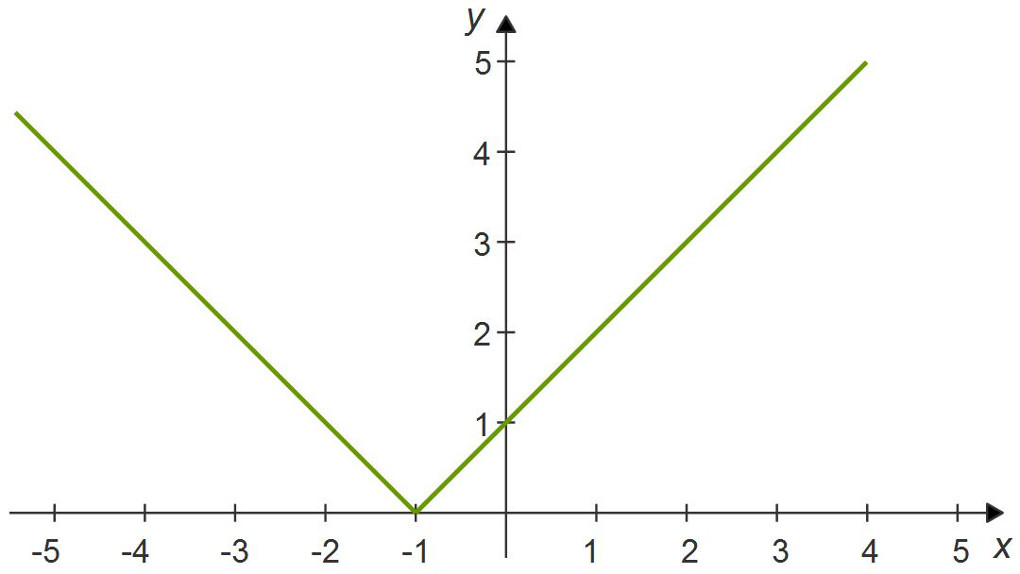
The vertex for this absolute value function is located at ( 0 , -1 ).