Side and Angle Conditions for a Triangle
- Side and Angle Conditions for a Triangle
- Side and Angle Conditions for a Triangle – Explanation
- Side and Angle Conditions for a Triangle – Examples
- Side and Angle Conditions for a Triangle – Practice
- Side and Angle Conditions for a Triangle – Summary
- Side and Angle Conditions for a Triangle – Frequently Asked Questions

Basics on the topic Side and Angle Conditions for a Triangle
Side and Angle Conditions for a Triangle
Triangles are among the simplest and most studied shapes in geometry, used in everything from architectural design to trigonometry classes. A triangle is a three-sided polygon, and its properties are fundamental to understanding many aspects of geometry. Constructing triangles may seem easy at first, but there are important factors to take into account.
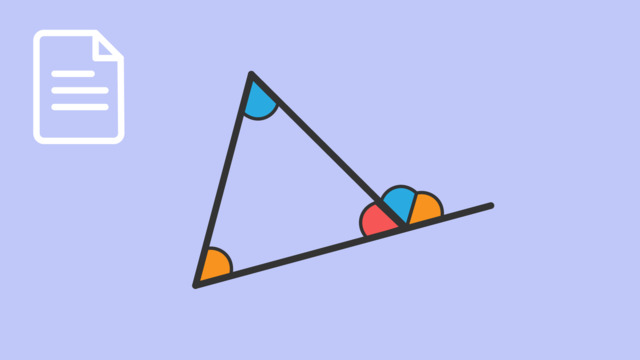
Triangles are shapes with three straight sides and three angles. The sum of the interior angles in a triangle always equals 180 degrees, and the length of any side must be less than the sum of the other two sides (triangle inequality theorem).
Side and Angle Conditions for a Triangle – Explanation
The properties of triangles vary depending on the lengths of their sides and the measures of their angles. Here are the basic rules and conditions:
| Rule Name | Description |
|---|---|
| Triangle Inequality Theorem | The sum of the lengths of any two sides of a triangle must be greater than the length of the third side. |
| Sum of Angles | The sum of the interior angles of a triangle is always 180 degrees. |
Side and Angle Conditions for a Triangle – Examples
Let's explore these concepts with an example:
Side and Angle Conditions for a Triangle – Practice
Practice what you have learned on your own!
Side and Angle Conditions for a Triangle – Summary
Key Learnings from this Text:
Triangles are three-sided figures with interior angles that add up to 180 degrees.
The triangle inequality theorem is crucial for understanding whether a set of three lengths can form a triangle.
Understanding these basic properties helps in solving more complex problems involving triangles and their properties in both academic studies and real-life applications.
Side and Angle Conditions for a Triangle – Frequently Asked Questions
Transcript Side and Angle Conditions for a Triangle
Pharaoh Ahmose enjoys a luxurious lifestyle, but there's something missing. He has heard stories of the kites which thrill the emperors in China. He wants a kite to call his own. So, Ahmose summons his engineers, and challenges them to build a triangular kite that will soar like a falcon. The engineers aren't sure they can actually form a triangle from the materials they have. They'll need to experiment to understand Side and Angle Conditions for a Triangle. The engineers are given three rods to form the supporting elements for the kite. The rods are 150 cm 70 cm and 30 cm long. We'll label the rods 'a', 'b,' and 'c,' respectively. Let's leave 'a,' the largest segment, here. Now let's try and assemble a triangle by placing the remaining segments on its ends. Can we complete a triangle? No! We can change the angles of 'b' and 'c' as much as we like, but no matter how much we try, they won't reach each other to complete a triangle. Together, they are just too short. Notice that 'b' and 'c' sum to be 100 cm which is less than 150 cm, the length of 'a'. What can we do to make this a complete triangle? Let's replace the 30 cm rod with one of 100 cm. Look! That makes a complete triangle! The two shorter sides of 70 cm and 100 cm sum to be 170 cm. That's greater than the longest side of 150 cm. In general, the two other sides must sum to be more than the longest side. Given three sides this is one of the conditions we must meet in order to form a triangle. The engineers want to try out different side lengths given two sides. Let's remove the 100 cm side and experiment. Given any two sides, what are the lower and upper limits for the third side? Let's start by finding the smallest measurement that this side, 'c,' can be. Let's rotate 'a' so that its angle is really small. Can 'c' be 80 cm? No! Because that would just give us a straight line and not a triangle. But could 'c' be 81 cm? Or even 85 cm? Yes! In fact, 'c' can be anything more than 80 cm. Because 80 is the difference of the two given sides, 150 and 70. Anything greater than that difference should be fine, right? Oh, but wait! What's the biggest that 'c' can be? If we swing side 'a' so that this angle is really big, then the side 'c' gets longer. Can 'c' be 220 cm? No! That just makes another straight line and not a triangle. So 'c' has to be less than 220 which is the SUM of the two given sides, 150 and 70. Anything less than the sum of the other two sides works. Now we can put these limits together. Given any two sides we can find the range of values for the third side. Any third side must be greater than the difference and less than the sum of the two given sides. In this case, 'c' must be greater than 80 and less than 220. But a triangle consists of more than just three sides. It also has three angles! How can we determine a triangle by just looking at two angles? Let's experiment again. First, let's construct a horizontal line segment 'AB'. Now, let's place our protractor at point A and mark a measure of 50 degrees. We'll use this mark to construct a ray, that is a line with a start point but no end point. Now from point 'B' let's measure a 150 degree angle. We'll construct a ray here as well. Do these two angles give us a triangle? No, clearly the rays will never intersect! Notice that the sum of the two angles is 200 degrees! But what if we made angle 'B' smaller? Notice that as the sum of the angles gets smaller we get closer to a triangle. In fact, any pair of angles in a triangle must sum to less than 180 degrees in order to form a triangle. Now the engineers understand the limits on the sides and angles they can use to build the triangular kite! Let's review side and angle conditions for forming a triangle as they complete their construction. Given three sides, the longest side must be less than the sum of the other two sides. Given any two sides, the third side must be greater than their difference, and less than their sum. Finally, two angle measurements determine many triangles provided that the sum of any two angles is less than 180 degrees. With all this knowledge the engineers construct a beautiful kite that soars like a falcon! But Ahmose, you can't just watch a kite, you've got to fly it.
Side and Angle Conditions for a Triangle exercise
-
Identify the measurements of the three sides of a triangle.
HintsTo form a triangle the sum of the two smaller sides must be greater than the longest side.
If we have a side of $150$ cm and the sum of the other two sides is less than that, they will not meet. For example, $70 + 30 = 100$
as $100 < 150$
There are $3$ correct answers here.
Solution- $11$ cm, $4$ cm and $12$ cm will form a triangle as $11 + 4 > 12$
- $8$ cm, $7$ cm and $13$ cm will form a triangle as $8 + 7 > 13$
- $6$ cm, $9$ cm and $11$ cm will form a triangle as $6 + 9 > 11$
- $5$ cm, $6$ cm and $12$ cm will not form a triangle as $5 + 6 < 12$, they will not meet.
- $4$ cm, $9$ cm and $13$ cm will not form a triangle as $4 + 9 = 13$, they form a straight line.(See image)
-
Find a possible measurement for a third side of a triangle, given two sides.
HintsThe third side has to ensure it creates a triangle.
In this example, one side is $9$ cm and the other side is $5$ cm. In order to form a triangle the third side needs to be $> 4$ as $4 + 5 = 9$ and that would form a line, not a triangle.
There are $2$ correct answers.
SolutionThe correct answer is $18$ cm and $20$ cm.
- $10 + 18 = 28$ and $28 > 25$
- $10 + 20 = 30$ and $30 > 25$
-
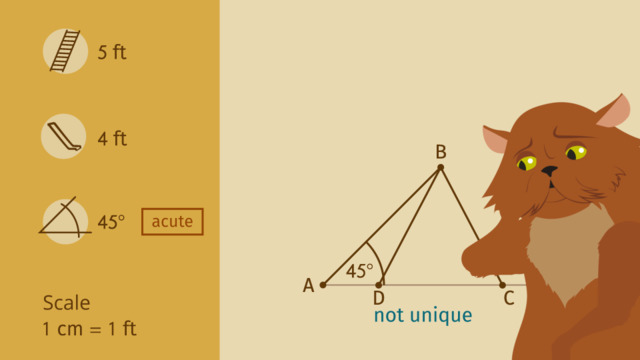
Determine the side and angle conditions to form a triangle.
HintsThe sum of the angles in a triangle is $180^\circ$. Anything more and the angles will not meet.
For example, $120 + 70 > 180$, therefore will not form a triangle.
The sides must meet, so the longest side should be smaller than the sum of the other two sides.
For example, sides of $10$ cm, $6$ cm and $3$ cm will not meet as $6 + 3 < 10$.
There are $3$ correct answers.
SolutionThe $3$ correct side and angle conditions are above.
The $2$ that are not correct are:
- angles in a triangle have a sum of $180^\circ$ and not $360^\circ$
- there can be a right angle in a triangle, but not in all triangles.
-
Create a triangular flowerbed.
HintsGrandpa will need two sides which will make a fairly large triangle. As you can see above, if the two sides are small, Grandpa will not be able to get many flowers in there.
The sum of the two sides will have to be longer than $28$ ft or they will not form a triangle.
For example, with sides of $2$ ft, $3$ ft and $7$ ft we cannot form a triangle.
SolutionSides $18$ ft and $21$ ft will add to $28$ ft to give a good-sized triangular flowerbed.
The others do not work as:
- they either will not meet - Sides $14$ ft and $12$ ft
- they form a straight line - Sides $14$ ft and $14$ ft
- or a very small triangle - Sides $10$ ft and $19$ ft
-
Identify the angle pair that would be impossible for a triangle.
HintsThe sum of the angles in a triangle is $180^\circ$.
For example $40 + 35 + 105 = 180^\circ$
We are looking for all $3$ angles in a triangle to $= 180^\circ$. Therefore, $2$ angles that have a sum greater than $180^\circ$ cannot form a triangle.
For example, if we have angles of $100^\circ$ and $110^\circ$ then that cannot possibly form a triangle as $100 + 110 > 180$.
SolutionThe correct answer is angles $132^\circ$ and $55^\circ$.
This will not work because
- angles in a triangle $= 180^\circ$
- here we have $132 + 55 = 187 > 180$
- the lines will not meet
- the other pairs of angles are $< 180^\circ$
-
Limits of sides to create a triangle.
HintsFor the lower limit it has to be greater than a value which will create a straight line.
For example, if one side is $9$ cm and the other side is $8$ cm then we could form a line if we added a side of $1$ cm.
- $9 - 8 = 1$.
For the upper limit it has to be greater than a value which will create a straight line when the two sides are added.
For example, if one side is $9$ cm and the other side is $8$ cm then we could form a line if we added $9 + 8 = 17$.
Therefore, we need the third side to be less than $17$ cm in order to form a triangle.
Solution- $a = 3$ cm and $b = 4$ cm has limits $4 - 3 < c < 4 + 3 = 1 < c < 7$
- $a = 4$ cm and $b = 7$ cm has limits $7 - 4 < c < 7 + 4 = 3 < c < 11$
- $a = 1$ cm and $b = 6$ cm has limits $6 - 1 < c < 6 + 1 = 5 < c < 7$
- $a = 2$ cm and $b = 6$ cm has limits $6 - 2 < c < 6 + 2 = 4 < c < 8$