Sequences of Translations


Basics on the topic Sequences of Translations
After this lesson, you will be able to perform a sequence of translations to move a figure to a desired location, or even map the figure onto itself.
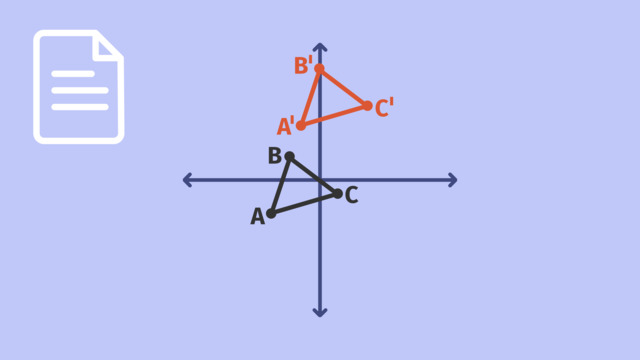
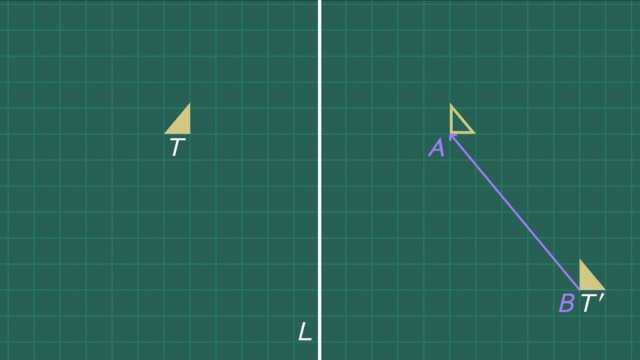
The lesson begins by teaching you that when you translate a figure along a vector then translate the resulting image along another vector, you have performed a sequence of translations. It leads you to learn that we can find single vectors that accomplish the same moves as any sequence. It concludes with performing a sequence of translations that maps the original image back onto itself.
Learn about sequences of translations by helping a mole named Doug journey to see the sun!
This video includes key concepts, notation, and vocabulary such as translation (moving a figure along a vector); vector (a directed line segment that tells you the length and direction of the move); reversing direction of a vector (given a vector AB, the vector BA has the same length but the opposite direction); mapping (translating a vector maps a figure to an image of the figure).
Before watching this video, you should already be familiar with translation and vectors.
After watching this video, you will be prepared to learn to perform sequences of transformations involving rotations and reflections.
Common Core Standard(s) in focus: 8.G.A.2 A video intended for math students in the 8th grade Recommended for students who are 13 - 14 years old
Transcript Sequences of Translations
The sun is coming up, as this family of moles is getting ready for bed. Doug, the youngest, likes a bedtime story before he falls asleep. His favorite tale is about the bright sun and its journey across the sky. Doug wants to see the sun from his favorite tale so he makes a plan to sneak to the surface. In order to find his way there, he needs to use a sequence of translations. Here's a diagram of Doug's underground neighborhood. We'll represent Doug with this polygon, 'D'. In order to translate polygon 'D', we need vector, 'u'. Vector 'u' is a directed line segment that tells us how far Doug will move, and in what direction. Let's translate polygon 'D' along vector 'u'. The image that results from this translation is called 'D' prime. Doug makes excellent progress towards the surface but this stone is an obstacle. We'll need a SECOND translation along a new vector to avoid the stone. Let's translate 'D' prime along vector 'v'. Translating D prime along v we see the resulting image let's call it 'D' double-prime. The sequence of translations along these two vectors brings Doug to the surface. Can you see a single translation, that would have brought Doug to the surface in one step? Translating 'D' along this vector gives the same result as translating along 'u', and 'v'. We'll call this vector 'AB'. When 'u' and 'v' are arranged as shown, 'AB' has the same starting point as 'u' and the same endpoint as 'v'. Ah, the sun is warm! But it's so bright and hard to see! Ok, maybe it's time to go. Doug is outta here! How can we help Doug return home quickly? Vector 'AB' gives us the correct distance, but it's the wrong direction. If we want the same distance as 'AB' but the opposite direction we can translate along 'BA', which means it starts here and ends here. We need to translate 'D' double-prime along vector 'BA'. This translation maps D double-prime back onto the original 'D'. We applied three translations to D. First, we translated 'D' along 'u' then along 'v' and then along 'BA'. This sequence of translations mapped 'D' onto itself. Doug ended his day where he started. Before we conclude his tale, let's review what we learned. When we translate a figure along a vector then translate its image along another vector this is called a sequence of translations. The figure is not changed by this process, only moved. We can always find a single vector that accomplishes the same sequence of translations in one step. We can also reverse the direction of vectors. Reversing vectors can help us create sequences of translations that map the original figure back onto itself. Doug is back home but his family is nowhere to be found! Oh no, they used their own sequence of translations to find their way to the surface, in search of Doug! These moles really dig translations! But their timing is a little off!