Sequences of Reflections and Translations

Basics on the topic Sequences of Reflections and Translations
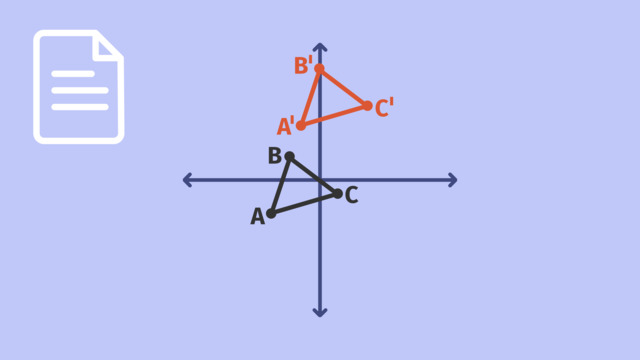
After this lesson, you will be able to reflect and translate an object, and reverse the sequence to map an image back to the original. The lesson begins by teaching you that the reflection of a reflection maps to the original. It leads students to learn changing the order of a sequence can change the image. It concludes by showing you that we can perform inverses in reverse order to map to the original.
Learn about reflections and translations by helping Tritri the robot get back to her spaceship!
This video includes key concepts, notation, and vocabulary such as reflection (a reflection across a line creates a mirror image with the same size and shape); translation (a translation moves an object along vector to create an image with the same size and shape); sequence (two more more transformations in order); and inverse (a transformation that maps an image back to the original).
Before watching this video, you should already be familiar with reflections across lines and translation along vectors, and prime notation for images of objects after transformation. After watching this video, you will be prepared to create sequences of transformations involving reflections, translations, and rotations.
Common Core Standard(s) in focus: 8.G.A.2 A video intended for math students in the 8th grade Recommended for students who are 13 - 14 years old
Transcript Sequences of Reflections and Translations
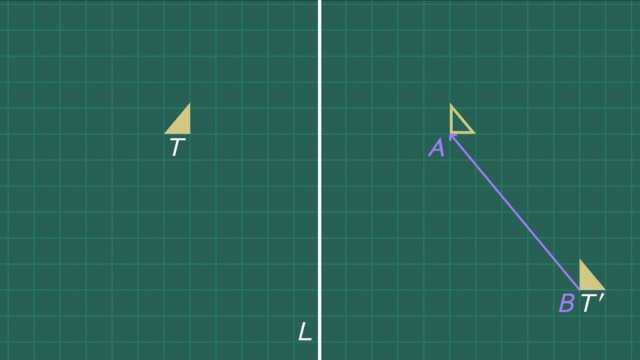
Deep in the darkness of space a curious light shines. Sasoma the cyborg is in her little spaceship, exploring the galaxy. She's not alone in this interstellar emptiness she's got her robot Trytry with her. Sasoma needs to teleport Trytry outside the spaceship for repairs. To transport Trytry to the right spot and back, Sasoma will need to perform a delicate sequence of reflections and translations. Three, two, one there she goes! Here is Trytry's original position, and here is her new position after teleportation. What happened? Trytry's teleportation was actually a geometric transformation. Recall that a transformation is a process which changes the position, and possibly the size and orientation, of a shape. Trytry is represented with triangle 'T.' What specific transformation occurred? T' was reflected across line 'L'. The IMAGE of 'T' after this reflection is called 'T' prime and it's the same size and shape as the original. Trytry has finished the repairs. So, how can we map 'T' prime back to its original position? The same reflection across line 'L' will reverse the transformation. A reflection is its own inverse! So it's easy for Sasoma to get Trytry back in the spaceship. But Trytry's work isn't done because there seems to be another thing to fix. How can Sasoma get Trytry to the issue? Sasoma starts by reflecting 'T' across line 'L' so that she's outside the ship as before. But to get to the desired location, we'll need a second transformation in this sequence: a translation. Which direction and how far does Trytry need to move? Along vector 'AB' should do the trick. So, 'T' prime is the image of 'T' after a reflection and a translation. This sequence of transformations moves Trytry to the right spot to fix the issue. Notice that with sequences of transformations, order matters. If we had translated first then reflected we'd have gotten an image in a very different location. Sasoma is eager to bring Trytry back to the ship so right away she reflects 'T' prime across line 'L'. Does this map Trytry back to her original location? Not at all! This could be a problem! How would you have mapped 'T' prime back to 'T'? Remember to map back to the original location, we should perform inverse transformations in reverse order. That means first translating along vector 'BA', the opposite direction from 'AB'. Then, we reflect across line 'L'. With sequences of transformations, mapping back to the original often requires multiple inverses performed in reverse order. Too bad Sasoma didn't get that right! In order to avoid mistakes let's review what we've learned about sequences of reflections and translations. A reflection creates a mirror image that's the same size and shape as the original. More than that, a reflection is its own inverse transformation. Remember with sequences of transformations order matters! For this reason, when we reverse sequences of transformations, we should often perform inverses in the reverse order. So, where is Trytry anyway? Well, I bet she's pretty T'ed off!