Reading and Writing Scientific Notation


Basics on the topic Reading and Writing Scientific Notation
Learning to read and write in scientific notation is important. Scientific notation allows very big and extremely small numbers to be understood and written in an easier form, making it easier for scientists to handle their results.
Scientific notation is of the form n•10a, where n, the coefficient, is always greater than or equal to 1, but less than 10. The 10 is called the base, and a is the exponent which is an indication of how many times the coefficient must be multiplied (or divided, when a is negative) by 10.
To convert a number into scientific notation, it is important to remember that the coefficient must always be greater than or equal to 1 and less than 10. The number of times we move the decimal point from its original position to the position where the number we are converting is greater than or equal to 1 and less than 10 is the exponent a of our base 10; the exponent is positive if the decimal point moved from the right towards the left and negative if the movement was from left to right. The number resulting from moving the decimal point is our coefficient n.
On the other hand, when we convert from scientific notation, if the exponent of the base 10 is positive, we move the decimal point of n to the right since a positive exponent indicates a very large number. If the exponent of the base 10 is negative, we move the decimal point to the left. In both cases, remember to write zeroes for every movement, or decimals places, where no digits are found. The number resulting from moving the decimal point of n is the number that was being represented by scientific notion.
Expressing and understanding numbers in scientific notation have extensive applications in many fields of Science, like Molecular Biology, Astronomy, and Engineering.
Work with radicals and integer exponents. CCSS.MATH.CONTENT.8.EE.3
Transcript Reading and Writing Scientific Notation
Dorothy is a really hardworking student. She has an internship at the prestigious Frank N. Stein Laboratory! At the lab, she works in the biology department, and her job is to observe how different types of bacteria grow. How fascinating!
Scientific Notation
It’s the end of Dorothy's internship, and she needs to write a final report about what she learned. She has all the facts, so she just needs to write up her findings in a neat report. Can you believe there are about 5 million, trillion, trillion bacteria on Earth? Wow! That's a lot of bacteria and that’s too many zeros to write down – her report is a mess. There’s another way! Dorothy can write this huge number in scientific notation*! Let’s review how to read and write numbers in scientific notation.
Simplifying very big and very small numbers
Just to review, scientific notation makes really BIG and really SMALL numbers easy to read and interpret. To write numbers in scientific notation, we write 'n', the coefficient, times 10, the base, raised to the power of 'a', which is the exponent. N' must be greater than or equal to 1 and less than 10. 10 raised to the 'a' power represents the number of times we must multiply 'n' by 10 to get back to the original number, the really big number with all the zeros.
To make this easier to understand, let’s look at an example: We'll write the number one million in scientific notation. To do this, move the decimal over until you have a coefficient that is greater than or equal to 1 and less than 10. Now, count the number of times you moved the decimal. Each time you move the decimal over one place value to the left, it's the same as multiplying by ten. So, since you moved the decimal six places to the left, we can write this as 1 x 10⁶.
Scientific Notation of really big Numbers
Let’s help Dorothy write her report. We’ll use the same process to this write this really big number in scientific notation. Scoot the decimal point over til you have a coefficient that is greater than or equal to 1 but less than 10, so this makes 'n' equal to 5.12. Now count the number of times you moved the decimal to the left and use that number to write the exponent using 10 as the base. We moved the decimal 30 places to the left. So we can write the number in scientific notation as 5.12 x 10³⁰.
Scientific Notation of really small Numbers
During her internship, Dorothy also observed the mass of various bacteria cells, and she learned that one really, really small bacteria has a teeny-tiny small mass. This critter is really small! Luckily for Dorothy, she can use scientific notation to write really small numbers too. We use the same process as before, but this time we move the decimal in the opposite direction. Each time you move the decimal over one place value to the right, it's the same as dividing by ten.
Remember, when the number in standard form is less than 1, the exponent is always a negative number. Our new number, 1.46, is greater than or equal to 1 but less than 10. Now count the number of places you moved the decimal point to the right, and write that number as the negative exponent. In scientic notation, the number is 1.46 x 10⁻¹⁴.
Converting from Scientific Notation to the Standard Form
How do you convert a number written in scientific notation to the standard form? As an example, let’s use 2.25 x 10⁴. We know this is 2.25(10)(10)(10)(10), but there's an easier way. Since the exponent is a positive number, we know the standard form will be a bigger number, so move the decimal over four places to the right 2.25 x 10⁴ is the same as 22,500.
Now that Dorothy used scientific notation to write her report, it’s much easier to read. Just look at that last fact. Wow! These particular bacteria have a very fast rate of growth. Now that's what I call a 'cultured' party!
Reading and Writing Scientific Notation exercise
-
Explain how to write numbers in scientific notation.
HintsThe power $10^a$ represents a product:
$10^a=\underbrace{10\times 10 \times... \times 10}_{a \text{ times}}$.
$a$ can either be positive or negative. An example for a number written in scientific notation with positive $a$ is $1.23\times 10^4=1,230$.
The following number is not written in scientific notation:
SolutionScientific notation makes really big and really small numbers easy to read and easy to interpret.
$~$
Any number can be written in the form $n\times 10 ^a$, where:
- $n$ is the coefficient.
- $10$ is the base.
- $a$ is the exponent.
The coefficient $n$ must be greater than or equal to $1$ and less than $10$.
-
Write the given numbers in scientific notation.
HintsAny number can be written in scientific notation;
i.e. $n\times 10^a$, where we must have that $1\le n<10$.
Keep in mind:
- $a$ is negative for a small number.
- $a$ is positive for a big number.
The following is an example for a scientific notation:
SolutionThe number of bacteria is given by $5,120,000,000,000,000,000,000,000,000,000$.
We scoot the decimal from right to left until we get a number which is greater than or equal to $1$ and less than $10$. In this case, we get $n=5.12$... we moved the decimal $30$ to the left!
With this information we can write our large number in scientific notation: $5.12\times 10^{30}$.
$~$
Similarly, we can write $0.0000000000000546$ in scientific notation.
We move the decimal point $14$ times to the right until we reach the first nonzero number, namely $5$. The coefficient is thus $n=5.46$ and the exponent is $a=-14$. Why $-14$? Well, we moved the decimal point to the right 14 times, meaning that we divided by $10$... $14$ times. Thus we get $a=-14$.
So we have that $0.0000000000000546=5.46\times 10^{-14}$.
-
Examine how the numbers are written in scientific notation.
HintsAny number can be written in scientific notation;
i.e. $n\times 10^a$, where we must have that $1\le n<10$.
An example of a number being converted into scientific notation is $1000000=1\times 10^6$.
The coefficient for a big number is given by the leading numbers not equal zero, with a decimal point after the first number.
For instance, with $314100000$ we have $n=3.141$.
For the exponent $a$ we either count how often we move the decimal point to the left or we count the positions after the leading $1$ until we reach the end of the number or a decimal point.
SolutionNumbers written in scientific notation are of the form
$n\times 10^a$, with $1\le n<10$.
$~$
For big numbers:
- $a>0$ can be found by the scooting of the decimal point to the left.
- The first numbers not equal zero with a decimal point after the first number is $n$.
- $14120000000=1.412\times 10^{10}$.
- $141.2=1.412\times 10^2$
For small numbers
- $a<0$ can be found by the numbers of scooting the decimal point to the right.
- The first numbers not zero after the decimal point with a decimal point behind the leading number is $n$.
- $0.001412=1.412\times 10^{-3}$
- $0.00000001412=1.412\times 10^{-8}$
-
Write the following numbers in scientific notation.
HintsIn the scientific notation, $n\times 10^a$, the exponent $a$ must be negative for small numbers.
An example of a number written in scientific notation is $0.000001=1\times 10^{-6}$.
The coefficient of $0.000003141$ when written in scientific notation is $n=3.141$.
SolutionA number written in scientific notation looks like $n\times 10^a$, where $1\le n<10$.
$~$
Let's figure out how to write the weights of Dorothy's objects in scientific notation:
- Grain of sand: $0.0000000007645=7.645\times 10^{-10}$
- Hair: $0.00001036=1.036\times 10^{-5}$
- Fingernail: $0.000441=4.41\times 10^{-4}$
- Ant: $0.0176=1.76\times 10^{-2}$
-
Describe the definition of scientific notation.
HintsIn the following picture, we see $t$ is raised by the power of $a$.
$t$ is the base and $a$ is the exponent.
SolutionScientific notation allows us to write very big or very small numbers in an easy to read and easy to understand way.
A number written in scientific notation looks like $n\times 10^a$, where:
- The coefficient $n$ must be greater than or equal to $1$ and less than $10$.
- The sign of the exponent $a$ is positive when a number is very big, or negative when a number is very small.
-
Determine the standard form of the number given in scientific notation.
HintsAn example of a big number written in scientific notation is $2.25\times 10^4=22500$.
For a big number, the exponent represents how much you have to move the decimal point to the right.
Let's look at the example above once again:
$\begin{array}{rcl} 2.25\times 10^4=2.25\times 10\times 10\times 10\times 10&=&22.5\times 10\times 10\times\\ & =&225\times 10\times 10\\ &=&2250\times 10\\ &=&22500 \end{array}$
SolutionLet's see how to convert scientific notation into a big (or small) number through the following example: $2.25\times 10^4$.
We already know that $10$ raised by $4$ can be written in the following way:
$2.25\times 10\times 10\times 10\times 10$.
Step by step, we have:
$\begin{array}{rcl} 2.25\times 10\times 10\times 10\times 10&=&22.5\times 10\times 10\times\\ & =&225\times 10\times 10\\ &=&2250\times 10\\ &=&22500 \end{array}$
$~$
In other words, we scoot the decimal point four times to the right. If we reach the number given by the coefficient and we still have to move the decimal point, we write down zeros.
$~$
So, for the given distances above we get:
- Earth to Saturn: $5.448\times 10^11=544800000000$
- Neptun to Sun: $1.479\times 10^{13}=14790000000000$
- Mercury to Sun: $1.903\times 10^{11}=190300000000$
- Jupiter to Earth: $3.171\times 10^{12}=3171000000000$


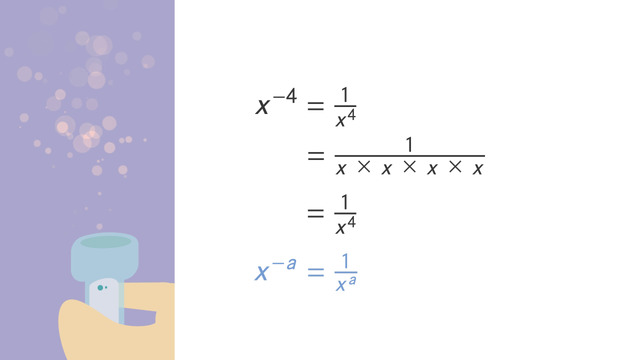













Thanks! We hope sofatutor continues to meet your educational needs! If you have any further comments or questions, you can always e-mail us at mathematics@sofatutor.com.
Great video!