Ratios of Fractions

Basics on the topic Ratios of Fractions
After this lesson, you will be able to convert complex fractions to unit rates using visual models to understand a scenario and solve one simple problem.
The lesson begins by teaching you how to use a clock model to find the unit rate involving complex fractions. It leads you to comparing rates. It concludes with using a double number line to compare ratios involving fractions.
Learn how to visualize ratios of fractions by helping Lorenzo and Yoko follow the same beat.
This video includes key concepts, notation, and vocabulary such as complex fractions (fractions with at least one fraction in the numerator or denominator), and visual models (clock models and double number lines) to find unit rates for ratios of complex fractions.
Before watching this video, you should already be familiar with calculating unit rates, interpreting ratios presented in verbal descriptions, ratio tables, graphs, or equations, converting from one representation to another, and assessing whether a relationship represented in any form is proportional or not.
After watching this video, you will be prepared to use division to find the unit rate and compare unit rates involving complex numbers.
Common Core Standard(s) in focus: 7.RP.A.1 A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
Transcript Ratios of Fractions
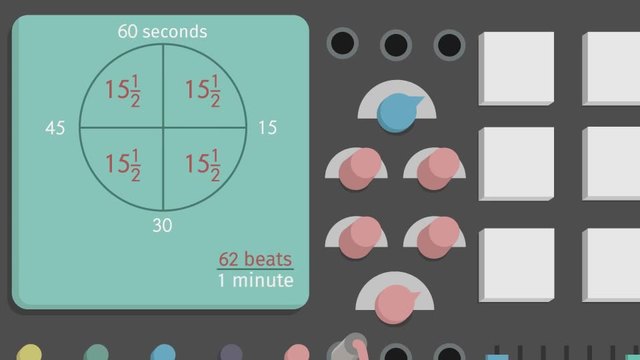
Lorenzo and Yoko live quiet, unremarkable lives by day, but by night, they’re an electronic music duo, laying down tracks in their basement studio. They're hard at work on their latest masterpiece, using homemade instruments they’ve designed themselves. Because they've never used these experimental instruments before, Lorenzo and Yoko will need to compare Ratios of Fractions to make sure they're following the same beat. If they don't want to sound like a trainwreck, Lorenzo and Yoko's instruments need to share equivalent ratios of beats per minute. Lorenzo’s digital drum kit is set to play 15 and a half beats every 15 seconds. So what's that in beats per minute? Well, let's get started by writing this ratio as a complex fraction. Because we want to compare this ratio in beats per minute, a clock model representing our whole, 60 seconds, can be used to find the equivalent unit rate. Since we're measuring Lorenzo's beats every 15 seconds and we know that 15 seconds are a quarter of a minute, let's divide up the clock into quarters. In each 15-second section, Lorenzo's drum kit plays 15 and a half beats. Now we can find the total number of beats per minute simply by adding all four sections together. That gives us a unit rate of 62 beats per minute. Let's compare this ratio to Yoko's and see if they're equivalent. Yoko's DIY synthesizer plays 5 and four-fifths beats every 12 seconds. To compare this rate to Lorenzo's, we're going to have to convert that to beats per minute. Once again, we can use this information to set up our clock model. Because we're measuring Yoko's beats every 12 seconds, we divide 60 seconds by 12 and find that there are 5 groups of 12 seconds in a minute. In each of these 12 seconds, Yoko's synthesizer plays 5 and four-fifths beats. Adding up the five sections, we get a ratio of 29 beats per minute. And now comparing this unit rate to Lorenzo's... ugh, these two instruments do NOT jibe together. But Lorenzo and Yoko are not ready to give up yet! Lorenzo cranks up the speed on his drum kit to 35 and a half beats every 15 seconds. To find out what that is in beats per minute, let's use another useful tool for dealing with ratios of fractions, the double number line. Using this model, we can put beats on top and seconds on the bottom. Then, to convert seconds to minutes, we can use repeated addition until we find an equivalent ratio with one term equal to 60 seconds. So, Lorenzo's beats go up in increments of 35 and a half as his seconds go up in increments of 15. Looking at the 60 seconds mark, we can find the unit rate of 142 beats per minute. Now Yoko's synth is set to play 23 and two-thirds beats every 10 seconds. Will that synchronize with Lorenzo's unit rate? Once again, we can use a double number line with beats on the top and seconds on the bottom to find if Yoko is using an equivalent ratio. We know that Yoko's synth plays 23 and two-thirds beats every 10 seconds so those are the first entries in the double number line. Now go up by increments of 23 and two-thirds on the beat line. 23 and two thirds plus 23 and two thirds gives us 47 and one third and adding 23 and two thirds again gives us 71. We can continue this process until the top number line is full. Then fill out our bottom number line in increments of 10 seconds until we reach 60. Would you look at that? Comparing this unit rate to Lorenzo's, the duo has done it: 142 beats per minute for both the drums and synth! Lorenzo and Yoko are in perfect sync! To review... When comparing ratios to see if they are equivalent, you may find yourself working with complex fractions. In these situations, clock models can be useful to help you determine a unit rate which will make comparisons easier. Just use division to figure out how many parts of your ratio make up the whole, then add all of your parts together to find an equivalent ratio that is your unit rate. Double number lines can also be useful when you want to compare ratios involving fractions. Start by adding the terms in your original ratio as the first entries on the number lines, then use repeated addition to find a set of equivalent ratios. Keep adding more equivalent ratios until you find one that can be converted to a unit rate. Now that Lorenzo and Yoko have found their groove, it's time for the big premier! For their, um, biggest...fan...