Ratio Problems with Discounts and Fees

Basics on the topic Ratio Problems with Discounts and Fees
After this lesson, you will be able to solve multi-step ratio problems.
The lesson begins by using ratios to find the new discounted price through the equation, New Price=Original Price – Discount Price. It leads you to using the equation, New Price/Original Price=1 – Discount Rate as another way to find the new price. It concludes with using a tape diagram to visualize the situation and find the total price.
Learn how to solve ratio problems by helping Showcase calculate discounts and fees.
This video includes key concepts, notation, and vocabulary such as markup (an increase in price), discount (a decrease in price), commission (a markup paid to the salesperson), fee (a markup paid to cover an external cost related to the transaction), and appreciation (a markup occurring due to market forces).
Before watching this video, you should already be familiar with calculating discounts and fees using percents, create complex fractions from a ratio of two fractions, simplify complex fractions using fraction bars, number lines and division, and solve multi-step problems involving part-to-part and part-to-whole ratios.
After watching this video, you will be prepared to learn specific problem solving with complex fractions drawn from tables and graphs of proportional relationships, as well as scale drawings and scale factors (geometric representations of proportionality).
Common Core Standard(s) in focus: 7.RP.A.1, 7.EE.B.4a, 7.RP.A.3 A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
Transcript Ratio Problems with Discounts and Fees
Welcome to this week's episode of "Boost My Lift." Today, our host Showcase will take this pickup truck, belonging to one of our viewers, and boost it up! Showcase will deck out the truck with wide screen monitors and a slammin' stereo system. And for the party in the back? A hot tub! But to make sure he stays under his budget of ten grand, Showcase will need to solve ratio problems with discounts and fees.
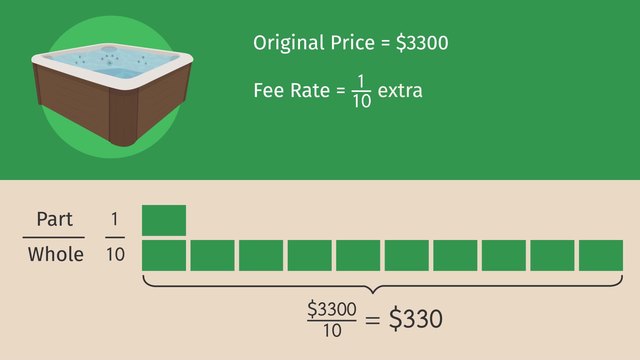
Showcase is a master at dealing with ratios, and he knows three different methods to deal with discounts and fees. On today's show, he's going to need all of them. You can never have too many monitors, so Showcase is going to buy 20 of 'em. The original total price would be 4,000 dollars but because he's ordering so many, he'll get a sweet discount of one fifth off. That means the ratio of the amount of the discount to the original price is one to five. So, what's the new price after the discount? We will first find the dollar amount of the discount, and then subtract this discount amount from the original price. Let's use the variable 'd' to represent the discount amount. The ratio of 'd' to the original price, 4,000 dollars, and the ratio one to five must be equivalent ratios Now we have to isolate the variable 'd' by multiplying both sides by 4,000 which gives us 'd' equal to 800. The discount amount is 800 dollars. That's some serious green! Now, subtract the discount amount from the original price to find the new price after the discount. 4,000 minus 800 equals 3,200 dollars. Wow! A scorching hot deal! This truck looks totally jacked with the new monitors! Now to add a stereo system. A new stereo system for the truck normally costs 1,200 dollars, but Showcase gets a nice discount when he buys stereos, because he's such a big star. How big of a discount? Three tenths off! Massive! But we are more interested in what he's actually going to pay, so what's the ratio of the new price to the original price? We can look at the original price as one whole. Then we can subtract the discount rate from one, which will give us the ratio of the new price to the original price. If the discount rate for the stereo system is three tenths, that means Showcase will pay seven tenths of the original price. Now let's use the variable 'n' to represent the new price, and set up our equivalent ratios. The ratio of 'n' to the original price, which was 1,200, is equal to the ratio of 7 to 10. Multipying both sides by 1,200 gives us 'n' equals 840. That means that Showcase only had to pay 840 dollars for the stereo system. Whoa, a stereo system for under a grand? That's a steal! Especially since it sounds like a million bucks! Now for the finishing touch... the hot tub! Showcase has a bodacious hot tub all picked out that costs 3,300 dollars. That thing weighs a ton, so there's a delivery fee of one tenth the normal price. Including delivery, what's the total cost of the hot tub? This time, Showcase is going to use a tape diagram. Remember, tape diagrams can be used to help us visualize equivalent ratios. We can set up a tape diagram using the ratio of part to whole that we already have of 1 to 10. But what is our equivalent ratio? We want to find the fee part, and we know the whole is represented with 10 pieces and is 3,300 dollars. So each piece of the tape diagram is found by taking the whole amount and dividing it by the number of pieces that represent the whole, 10. That means each piece of the tape is worth 330 dollars. Because this piece represents the part that is our fee, we can see that the fee is 330 dollars. Adding that to the original price we get the total, including the fee, to be 3,630 dollars. Wow! That's one hot ride. Let's see if Showcase made it happen under his budget of ten thousand dollars. 3,200 for the monitors plus 840 for the sound system plus 3,630 for the hot tub comes to 7,670. Way to rock the discounts, Showcase! Before we show this tricked-out truck to our lucky viewer, let's review our methods. We used three different methods to find the new price after applying discounts and fees. The first method involves using equivalent ratios to find the discount amount. Then we subtract the discount amount from the original price to get the new price. The second method involves first finding the ratio of the new price to the original price and then using equivalent ratios to find the new price.
For method 3, we visualized the situation using a tape diagram. When using tape diagrams, we first set up the number of blocks representing the ratio of the part to the whole. We then calculate how much each block is worth, which allows us to see how much the fee, and therefore total price, is. Now it's time for our lucky viewer to check out this tricked-out truck! Um... ma'am? Are you sure this truck is up to your specifications? Most def!













Granny SLAY
OMG Yassssssssssss
"MOST DEF" OMGGGGGGGGGG IM DYING!!!!!😂🤣💀💀
OMGGGGG THE "DRIPPED OUT" GRANNY!!!! AWWWWW!🤣🤣
YEAAAHHHH BOYYYYYYYYYY
HECK YEAH MR SQUEAKS!!!