What are Proportional Relationships?


Basics on the topic What are Proportional Relationships?
After this lesson, you will be able to recognize proportional relationships and be able to represent them using equations.
The lesson begins by teaching you that a proportion is a statement that relates two quantities. It leads you to learn how to set-up an equation representing a given proportion using variables and given values. It concludes with the usage of cross-multiplication to solve the equation.
Learn about proportions by watching Aunt Sally join her niece Flo in a race.
This video introduces new concepts, notation, and vocabulary such as proportional relationship, which is a mathematical relation between two quantities.
Before watching this video, you should already be familiar with writing ratios as factions, constants and variables, cross multiplication process, and solving equations.
After watching this video, you will be prepared to solve real-world problems that involve quantities represented by proportional relationships, including applications of percentage.
Common Core Standard(s) in focus: 7.RP.A.2 A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
Transcript What are Proportional Relationships?
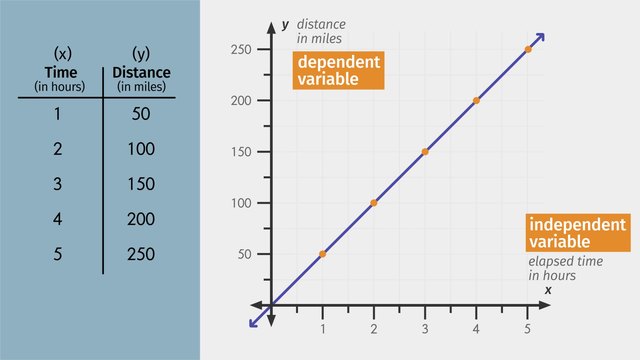
My dear Aunt Sally, who sometimes gets a little confused, is reading a postcard she just got from her niece, Flo. Flo is writing to see if her aunt would like to come watch her run her first 5K race. Apparently, 5 kilometers is only about 3.1 miles, so Aunt Sally decides to surprise her niece and run WITH her in the race. To figure out how long it will take Aunt Sally to run the 5K, we're going to need to use proportional relationships. Let’s look at the facts. Flo figures it will take her nine minutes to run one mile. We can write this information as a ratio. Remember, the numbers in a ratio tell us how much there is of one quantity when compared to another. We could use a variety of different formats, but let's write our ratio as a fraction, comparing time to distance. Flo runs at a constant rate of 9 minutes for every 1 mile. Since the rate will never change, we can say that the relationship between time and distance is proportional. Just like equivalent fractions, a proportion is a statement that relates two quantities. So, how long will it take Flo to run the race? We know that she wants to run 3.1 miles, so we can plug that in for distance. We want to find the time it will take, so we will let 't' equal time. We can solve for 't' using cross-multiplication. First, we multiply the numerator on the left side of the equal sign by the denominator on the right side of the equal sign. Then, we set that equal to the product of the numerator on the right side and the denominator on the left side. 9 times 3.1 is 27.9. So this means it will take Flo 27.9 minutes to complete the race. Let's just round that up to 28 minutes to make things easier. But what about Aunt Sally? Unlike her niece Flo, Aunt Sally is a little out of practice. So it takes her 13 minutes to run 1 mile. Let’s write this constant rate as a ratio. If Flo can run the race in 28 minutes, where will Aunt Sally be when her niece finishes? Just like we did before, we can write a proportion and then solve for the unknown quantity by using cross-multiplication. This time 'd' is equal to the distance in miles Aunt Sally can run in 28 minutes, while running at her constant rate of 13 minutes per mile. Just like before, cross multiply and set the two products equal to each other, giving us 13d is equal to 28. Next, use the opposite operation of division to isolate the 'd'. Dividing both sides by 13, 'd' is equal to 2.15 miles. Which means Aunt Sally can go 2.15 miles in 28 minutes. I guess Flo will be waiting for her at the finish line! But how long will Sally need to finish the whole race? To find out, again we can set up a proportion using the constant rate 13 minutes for every mile. This time, ‘t’ is equal to the time it will take Sally to run 3.1 miles. Cross-multiply like we did before, giving us 13 times 3.1 is equal to 't'. So it looks like Aunt Sally will finish the race in just over 40 minutes, if she runs at a constant rate of 13 minutes per mile. That's not bad for somebody who's a little out of practice! So, to review... A proportional relationship describes a relationship between two or more numbers, like the relationship between time and distance. When solving problems involving proportional relationships, you first have to set up your proportion, then substitute in the known values, cross-multiply and simplify. It looks like Aunt Sally has finished the race, or actually, the race has finished HER.
What are Proportional Relationships? exercise
-
Describe how to set-up and solve proportional relationships.
HintsThe ratio of numbers $2$ and $3$ can be written in the following forms:
- $2$ to $3$
- $2:3$
- $\frac{2}{3}$
If it takes Flo $7$ minutes to run $1$ mile, how long does it take her to run $5$ miles?
- The proportion is $\frac{7}{1}=\frac{t}{5}$, where $t$ represents time.
- Cross multiply: $7(5)=1\cdot t$
- Solve: $t=35$
If it takes Aunt Sally $11$ minutes to run $1$ mile, how far will she be in $35$ minutes?
- The proportion is $\frac{11}{1}=\frac{35}{d}$, where $d$ represents distance.
- Cross multiply: $11d=35$
- Solve: $t=3.18$
SolutionA Proportional Relationship for Flo.
Flo figures it will take $9$ minutes to run $1$ mile.
This information can be written as a ratio because it tells us how much there is of one quantity when compared to another.
The ratio as a fraction is, $\frac{9~\text{minutes}}{1~\text{mile}}$.
Since the rate will never change, we can write a proportional relationship between time and distance.
Let $t$ equal time, $\frac{9~\text{minutes}}{1~\text{mile}}=\frac{t}{3.1~\text{miles}}$.
To solve for $t$, multiply the numerator on the left by the denominator on the right, and the numerator on the right by the denominator on the left.
This is called cross multiplying, $9(3.1)=1\cdot t$.
It will take Flo is approximately $28$ minutes to run the $5$k.
A Proportional Relationship for Aunt Sally
What about Aunt Sally? If it takes her $13$ minutes to run $1$ mile, where will Aunt Sally be in $28$ minutes, when Flo finishes the race?
We can write another proportional relationship between time and distance.
This time we want to solve for the distance which we can represent with the variable $d$.
The proportion is represented by the equation,
- $\frac{13}{1}=\frac{28}{d}$.
- $13d=28$.
-
Solve the proportion for the missing variable.
HintsTo solve a proportion, multiply the numerator on the left by the denominator on the right, and the numerator on the right by the denominator on the left. This is called cross multiplying.
After cross multiplying a proportion, simplify the equation, then use the opposite operation, division, to solve for the variable.
The following steps are used to solve the proportion, $\frac{t}{24}=\frac{9}{15}$:
- Cross multiply: $24(9)=15t$
- Simplify: $216=15t$
- Solve: $t=14.4$
SolutionTo solve a proportion, multiply the numerator on the left by the denominator on the right, and the numerator on the right by the denominator on the left. This is called cross multiplying.
Simplify the equation, then use the opposite operation, division, to solve for the variable.
1. $\frac{5}{t}=\frac{3}{25}$
- Cross multiply: $5(25)=3t$
- Simplify: $125=3t$
- Solve: $t=41.7$
- Cross multiply: $20(16)=7t$
- Simplify: $320=7t$
- Solve: $t=45.7$
- Cross multiply: $9(19)=4t$
- Simplify: $171=4t$
- Solve: $t=42.8$
- Cross multiply: $41t=87(19)$
- Simplify: $41t=1653$
- Solve: $t=40.3$
- Cross multiply: $75t=350(8)$
- Simplify: $75t=2800$
- Solve: $t=37.3$
-
Calculate and sort the proportional relationships.
HintsThe numbers in a ratio tell us how much there is of one quantity when compared to another.
For example, $\frac{\text{miles}}{\text{hours}}$.
To solve a proportion, multiply the numerator on the left by the denominator on the right, and the numerator on the right by the denominator on the left. This is called cross multiplying.
Rita can read $19$ pages in $30$ minutes. How long will it take her to read a $250$ page book?
- Set up the proportional relationship: $\frac{19}{30}=\frac{250}{t}$
- Cross multiply: $19t=30(250)$
- Simplify: $19t=7500$
- Solve: $t=394.7$
- It will take Rita about $395$ minutes to finish reading the book.
SolutionWrite each word problem as a proportional relationship between two ratios, then solve for the unknown.
It is always important to make sure that both numerators and denominators are consistent, $\frac{\text{miles}}{\text{hour}}=\frac{\text{miles}}{\text{hour}}$ or $\frac{\text{hours}}{\text{miles}}=\frac{\text{hours}}{\text{miles}}$.
To solve a proportion, multiply the numerator on the left by the denominator on the right, and the numerator on the right by the denominator on the left. This is called cross multiplying.
1. Ivanka is making cookies for her friends. The recipe calls for $2\frac{1}{4}$ cups of flour for $48$ servings. Ivanka wants to make $64$ servings. How many cups of flower does Ivanka need?
- Let $c$ represent the cups of flour.
- Set up the proportional relationship: $\frac{2\frac{1}{4}}{48}=\frac{c}{64}$
- Cross multiply: $2\frac{1}{4}(64)=48c$
- Simplify: $144=48c$
- Solve: $c=3$
- Ivanka needs $3$ cups of flour to make $64$ servings.
- Let $m$ represent the number of miles.
- Set up the proportional relationship: $\frac{10}{32}=\frac{m}{57}$
- Cross multiply: $10(57)=32m$
- Simplify: $570=32m$
- Solve: $m=17.81$
- Marty will drive $17.81$ miles in $57$ minutes.
- Let $p$ represent the number of pancakes.
- Set up the proportional relationship: $\frac{22}{8}=\frac{p}{14}$
- Cross multiply: $22(14)=8p$
- Simplify: $308=8p$
- Solve: $p=38.5$
- Rae finds that $38.5$ pancakes will feed $14$ people.
- Let $d$ represent the amount of money she will earn.
- Set up the proportional relationship: $\frac{15.25}{1}=\frac{d}{36}$
- Cross multiply: $15.25(36)=d$
- Solve: $d=549$
- Sybille will earn $549$ after working $36$ hours.
-
Find the correct proportions, equations, and answer.
HintsMake sure that both numerators and denominators in the proportional relationships are consistent.
For example, $\frac{\text{miles}}{\text{hour}}=\frac{\text{miles}}{\text{hour}}$ or $\frac{\text{hours}}{\text{miles}}=\frac{\text{hours}}{\text{miles}}$.
To solve a proportion, cross multiply the numerators and denominators.
Johann can run $3$ miles in $32$ minutes. How long will it take him to run $8.5$ miles?
- Set up the proportional relationship: $\frac{3}{32}=\frac{8.5}{t}$
- Cross multiply: $3t=32(8.5)$
- Simplify: $3t=272$
- Solve: $t=90.7$
- It will take Johann about $91$ minutes to run $8.5$ miles.
SolutionAnna sells homemade cherry pies at a weekly bake sale. Last Sunday she sold $14$ pies and made $ \$108.50$. If she makes $ \$209.25$ the following week, how many pies did she sell?
Proportions
Since Anna sells $14$ pies for $ \$108.50$, the ratio is, $\frac{14}{108.50}$.
Anna wants to know how many pies she needs to sell to make $ \$209.25$ so she sets up the proportion, $\frac{14}{108.50}=\frac{x}{209.25}$, where $x$ represents the number of pies.
It is always important to make sure that both numerators and denominators are consistent, $\frac{\text{pies}}{\text{total sales}}=\frac{\text{pies}}{\text{total sales}}$ or $\frac{\text{total sales}}{\text{pies}}=\frac{\text{total sales}}{\text{pies}}$.
This means that another way to write the proportion is, $\frac{108.50}{14}=\frac{209.25}{x}$.
Equations
To solve a proportion, cross multiply the numerator on the left by the denominator on the right, and the denominator on the left by the numerator on the right.
- 14(209.25)=108.50x$
- $108.50x=2,929.50$
To solve the proportion, use opposite operations to isolate the variable $x$.
- Divide both sides by $108.50$,
- $x=27$.
-
Identify which pairs of ratios are proportional to each other and which are not.
HintsTwo ratios are proportional to each other if they are equivalent ratios.
$\frac{18}{3}$ and $\frac{6}{1}$ are proportional because they both reduce to the fraction $\frac{6}{1}$.
$\frac{8}{12}$ and $\frac{3}{4}$ are not proportional to each other because they do not reduce to the same fraction, so they are not equivalent ratios.
SolutionProportional
The following pairs of ratios are proportional to each other because both reduce to the same fraction, meaning that they are equivalent ratios:
- $\frac{4}{8}$ and $\frac{5}{10}$ simplifies to $\frac{1}{2}$ and $\frac{1}{2}$.
- $\frac{2}{8}$ and $\frac{4}{16}$ simplifies to $\frac{1}{4}$ and $\frac{1}{4}$.
- $\frac{10}{5}$ and $\frac{16}{8}$ simplifies to $\frac{2}{1}$ and $\frac{2}{1}$.
- $\frac{18}{4}$ and $\frac{9}{2}$ simplifies to $\frac{9}{2}$ and $\frac{9}{2}$.
The following relationships are not proportional because simplifying the original ratios results in non-equivalent ratios:
- $\frac{5}{12}$ and $\frac{12}{3}$ simplifies to $\frac{5}{12}$ and $\frac{4}{1}$.
- $\frac{3}{9}$ and $\frac{4}{10}$ simplifies to $\frac{1}{3}$ and $\frac{2}{5}$.
- $\frac{15}{5}$ and $\frac{5}{15}$ simplifies to $\frac{3}{1}$ and $\frac{1}{3}$.
- $\frac{1}{9}$ and $\frac{27}{3}$ simplifies to $\frac{1}{9}$ and $\frac{9}{1}$.
-
Solve the real-world proportion problems.
HintsIt may be necessary to convert units to make them the same.
For example:
- $4$ feet $3$ inches is $15$ inches
- $3$ hours and $20$ minutes is $200$ minutes.
Make sure that both numerators and denominators in the proportional relationships are consistent.
For example, $\frac{\text{miles}}{\text{hour}}=\frac{\text{miles}}{\text{hour}}$ or $\frac{\text{hours}}{\text{miles}}=\frac{\text{hours}}{\text{miles}}$.
Rita can sew $3$ blankets in $5\frac{1}{2}$ days. How many days will it take Rita to sew $13$ blankets?
- Set up the proportional relationship: $\frac{3}{5\frac{1}{2}}=\frac{13}{d}$
- Cross multiply: $5\frac{1}{2}(13)=3d$
- Simplify: $71\frac{1}{2}=3d$
- Solve: $d=23.83$
- It will take Johann about $23.8$ days to make $13$ blankets.
Solution1. Dr. Cheng prides himself on seeing many patients in one day. On a normal day, he evaluates $3$ patients in $1$ hour and $15$ minutes. How many patients will Dr. Cheng see in $6$ hours and $40$ minutes?
- Let $p$ represent the number of patients.
- Convert hours to minutes: $1$ hour and $15$ minutes is $75$ minutes, and $6$ hours and $40$ minutes is $400$ minutes.
- Set up the proportional relationship: $\frac{3}{75}=\frac{p}{400}$
- Cross multiply: $3(400)=75p$
- Simplify: $1,200=75p$
- Solve: $p=16$
- Dr. Cheng will see $16$ patients in $6$ hours and $40$ minutes.
- Let $w$ represent the number of water bottles.
- Set up the proportional relationship: $\frac{3}{9}=\frac{5}{w}$
- Cross multiply: $3w=9(5)$
- Simplify: $3w=45$
- Solve: $w=15$
- The $5$ friends need to bring $15$ water bottles.
- Let $p$ represent the packs of baseball cards.
- Set up the proportional relationship: $\frac{12}{1}=\frac{540}{p}$
- Cross multiply: $12p=1(540)$
- Simplify: $12p=540$
- Solve: $p=45$
- Aaron bought $45$ packs of baseball cards.
- Let $h$ represent the height of the model car.
- Convert feet to inches: $10\frac{3}{4}\text {feet}=129\text {inches}$ and $4\frac{1}{2}\text {feet}=54\text {inches}$
- Set up the proportional relationship: $\frac{129}{54}=\frac{5}{h}$
- Cross multiply: $129h=54(5)$
- Simplify: $129h=270$
- Solve: $h=2.09$
- Sarita needs to make her model car $2.1$ inches high.