Properties of Inequalities

Properties of Inequalities exercise

• Describe the addition and subtraction properties of inequalities.

  Hints

  Let's look at the following example:

  Paul would like to buy some new headphones.

  Type A headphones cost $20$ dollars, and type B headphones cost $25$ dollars.

  First, we consider $20<25$.

  The price of each increases by $4$ dollars.

  After the increase, type A cost $24$ dollars and type B $29$ dollars.

  Think about the corresponding inequality symbol. Did it change?

  Given $20<25$ we known that $20+4<25+4$ which is the same as $24<29$. What happened to the inequality symbol when we added $4$ to both sides?

  Prices of headphones that were $24$ and $29$ dollars have now decreased by $10$ dollars each.

  This leads to $14$ dollars for type A headphones and $19$ dollars for type B.

  Think about which inequality symbol we need before they decreased in price and after we took away $10$ dollars from each side.

  Given $24<29$ we known that $24-10<29-10$ which is the same as $14<19$. What happened to the inequality symbol when we subtracted $10$ from both sides of the inequality?

  When using the addition or subtraction property of inequalities the inequality symbol remains the same (we keep the inequality symbol).

  Solution

  An inequality is given by $a<b$ or $a>b$. No matter which inequality symbol we have, neither the addition nor the subtraction of any number on both sides of the inequality changes the inequality symbol.

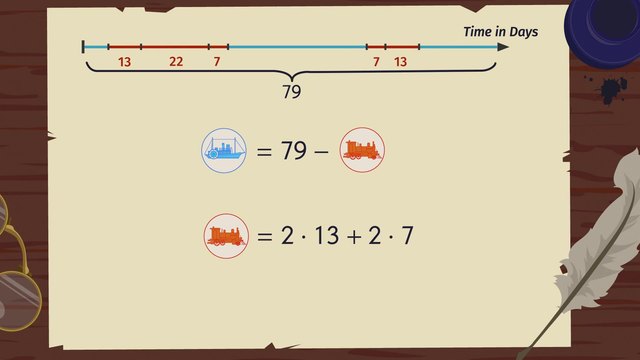
  To the right you can see an application of the Addition Property of Inequality:

  • We know $90<142$.
  • When adding $20$ on both sides, you have to keep the sign:

  • $20+90<142+20$

  or

  • $110<162$

  Likewise, we can consider the Subtraction Property of Inequality:

  • $110<162$
  • Subtracting $30$ on both sides leads to
  • $110-30<162-30$

  or

  • $80<132$.

  Notice how we keep the inequality symbol the same.

• Examine the multiplication and division property of inequalities.

  Hints

  Paul is looking to buy earphones, and has two choices:

  • type A $15$ dollars
  • type B $20$ dollars

  No matter which pair he decides to buy, his parents will pay for half. That means $7.50$ dollars for the type A earphones and $10$ dollars for the type B earphones. Written as inequalities, both the original price and the price when his parents paid for half, what would happen to the inequality sign?

  What happens to a number when you multiply it or divide it by a negative number?

  When you multiply or divide a number by a negative number the number changes in quantity by that amount and become the opposite. For example $2$ times $-3$ becomes $3$ times the size of $2$ and the opposite. $2 \times -3 = -6$. So, when dealing with inequalities think about when opposites occur what would happen to the relationship represented by the inequality.

  Solution

  Adding or subtracting any number doesn't change the inequality symbol:

  • $2<4$, so $2+4<4+4$
  • $2<4$, so $2-4<4-4$

  But what happens to the inequality symbol if you multiply or divide on both sides. This depends on the sign of the number by which you multiply or divide.

  Multiplication and Division of Positive Numbers Property of Inequality

  If you multiply both sides of an inequality by a positive number or you divide both sides by a positive number you can keep the inequality symbol.

  Let's have a look at the antelopes example:

  • $80<132$
  • Now we multiply both sides by $\frac78$. That's the same as multiplying by $7$ and dividing by $8$, both positive numbers.

  $\begin{array}{rcl} \frac78\cdot 80&<&\frac78\cdot 132\\ \frac{7\cdot 10 \cdot 8}{8}&<&\frac{7\cdot 33\cdot 4}{2\cdot 4}\\ 7\cdot 10&<&115.5 \end{array}$

  Multiplication and Division of Negative Numbers Property of Inequality

  Make sure to pay attention to the sign. If you multiply both sides of an inequality by a negative number or divide both sides by a negative number, you have to change the inequality symbol.

  To see this in action, let's have a look at the following example:

  • $-4<6$
  • Now we divide both sides by $-2$ and get $2$ ??? $-3$.
  • What inequality symbol should we use?
  • $2$ is greater than $-3$. This gives us $2>-3$.
  • You see the sign changed from $<$ to $>$.

• Determine the corresponding inequality.

  Hints

  You only have to flip the inequality symbol if you multiply or divide both sides by negative numbers.

  Pay attention to the inequality sign given the following example $10<20$:

  • $10+2<20+2$ is the same as $12<22$
  • $10-3<20-3$ is the same as $7<17$
  • $2=10\div 5<20\div 5=4$ is the same as $2<4$
  • $-2\cdot 10>-2\cdot 20$ is the same as $-20>-40$ inequality is now flipped from original
  • $\frac{10}{-2}>\frac{20}{-2}$ is the same as $-5>-10$ inequality is now flipped from original

  Solution

  This summary can help you when dealing with inequalities. You have to remember to flip the symbol if you either multiply or divide by a negative number.

  Therefore, using the inequality $2<7$:

  • Adding $3$ leads to $2+3<7+3$, or $5<10$. Here you have to keep the symbol.
  • Multiplying by $-2$ leads to $-2\cdot 2>-2\cdot 7$, or $-4<-14$. Here you have to flip the symbol.
  • Subtracting $4$ leads to $2-4<7-4$ and so $-2<3$. Here you have to keep the symbol.
  • Dividing by $-10$ leads to $2\div(-10)>7\div(-10)$, or $-0.2>-0.7$. Once again you have to flip the symbol.

• Check the corresponding application of properties of inequalities.

  Hints

  You can only highlight the last symbol. Decide if it's correct or not.

  Keep in mind that you only have to flip the inequality symbol if you multiply or divide by negative numbers.

  • Adding $5$ leads to $5+5<10+5$, or $10<15$.
  • Subtracting $5$ leads to $5-5<10-5$, or $0<5$.
  • Multiplying $5$ leads to $5\cdot 5<10\cdot 5$, or $25<50$.
  • Dividing by $-5$ leads to $5\div(-5)>10\div (-5)$, or $-1>-2$. Here you have to flip the symbol.

  Solution

  $\mathbf{-14 < -2}$

  If you add or subtract any number you can keep the inequality symbol. So you get, subtracting $6$:

  • $-14-6<-2-6$
  • $-20<-8$

  $\mathbf{3 < 18}$

  Dividing by a negative number, i.e. $-3$, you have to remember to flip the inequality symbol.

  • $3\div (-3)>18\div(-3)$
  • $-1>-6$

  $\mathbf{-4<-2}$

  When multiplying by a positive number, keep the symbol even if both sides of the inequality are negative.

  • $-4\cdot 2<-2\cdot 2$
  • $-8<-4$

  $\mathbf{-1<1}$

  When adding $3$, keep the symbol.

  • $-1+3<1+3$
  • $2<4$

  Multiplying by a negative number, i.e. $-1$, flips the symbol because the relationship is now opposite.

  • $-2>-4$

• Identify the inequality symbols you have to use.

  Hints

  Remember, just like with crocodiles, the inequality symbol opens to, "eats," the bigger number.

  First, simplify the numbers. Then, read the numbers with the symbol where $<$ reads "less than," and $>$ reads "greater than."

  If you're having difficulty, plot the numbers on a number line to compare.

  For example, if we plot $-6$ and $-12$ we can see that $-6 > -12$.

  • $<$ "is less than" and can also be read as "is under" or "is fewer than"
  • $>$ "is greater than" and can also be read as "is more than," "is over," or "exceeds."

  Solution

  • $77 > 65$, $77$ is greater than $65$.

  • $-10 < -5$, $-10$ is less than $-5$.

  • $3 < 7$, $3$ is less than $7$.
  • $3+2 < 7+2$ (simplify) $5$ is less than $9$. Notice how when we added the same number to both sides of the inequality we kept the inequality symbol the same because the relationship stayed the same.

  • $2 > -7$, $2$ is greater than negative $7$.
  • $2+7 > -7 +7$ (simplify) $9$ is greater than $0$. Notice again, that we added the same number to both sides of the inequality and the symbol remained the same.

  • $13< 25$, $13$ is less than $25$.
  • $13-12 < 25-12$ (simplify), $1$ is less than $13$.

  • $10 \cdot 5 > 4 \cdot 5$ (simplify), $50$ is greater than $20$.
  • $10 > 4$, $10$ is greater than $4$. Notice that when we multiply both sides of the inequality by $5$ that the inequality stays the same. ($5$ is a positive number)

  • $55<70$, $55$ is less than $70$.
  • $55\div (-5) > 70\div(-5)$, (simplify) $-11$ is greater than $-14$. Notice that when we divided both sides by a negative $5$ the inequality symbol changed directions. Because of the negative division the relationship changed between the numbers.

  Keep the following properties in mind:

  • Addition Property of Inequalities: The addition of any number on both sides of an inequality keeps the inequality symbol.
  • Subtraction Property of Inequalities: The subtraction of any number on both sides of an inequality keeps the inequality symbol.
  • Multiplication or Division Properties of Positive Number Inequalities: Multiplication or division by any positive number on both sides of an inequality keeps the inequality symbol.
  • Multiplication or Division Properties of Negative Number Inequalities: Multiplication or division by any negative number on both sides of an inequality changes the inequality symbol.

• Indentifying the properties of inequalities.

  Hints

  Here you can see the summary.

  Keep in mind: Only multiplying or dividing by negative numbers flips the inequality symbol.

  Solution

  Independent of the sign of $a$ and $b$ we can state the following:

  • Adding $c$ leads to $a+c<b+c$.
  • Subtracting $c$ leads to $a-c<b-c$.
  • Multiplying by positive $c$ leads to $a\cdot c<b\cdot c$.
  • Likewise, dividing by positive $c$ leads to $a\div c<b\div c$.

  We have two cases which lead to flipping the inequality symbol.

  • Multiplying by negative $c$ leads to $a\cdot c>b\cdot c$.
  • Also, dividing by negative $c$ leads to $a\div c>b\div c$.