One Point, One Slope, One Line
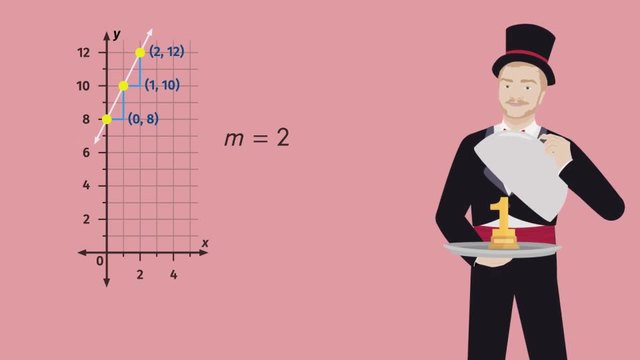

Basics on the topic One Point, One Slope, One Line
Given a point and a slope, a line can be drawn by plotting the point on a coordinate plane, then using the slope to get a second, or even a third or a fourth, point, and then finally connecting the points to produce a line. It’s important to note that two points always determine a line and that the slope is constant anywhere throughout the line. With this, we can see that given one point and one slope, we will always get one, unique line. Learn how to graph the line determined by a point and a slope by watching Thomas, a shoddy mathemagician, performs tricks to please the crowd. Common Core Reference: CCSS.MATH.CONTENT.8.F.B.4
Transcript One Point, One Slope, One Line
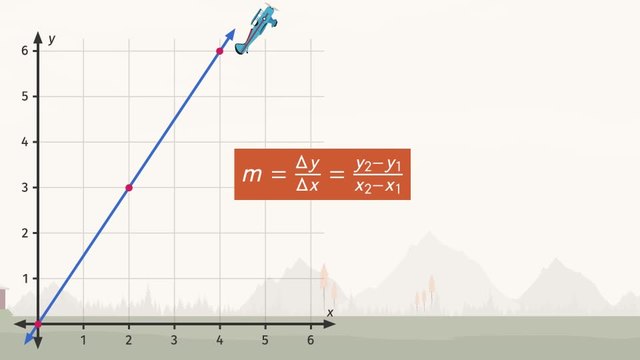
Come one, come all to see the AMAZING Shoddy Mathemagician, Thomas, performing this week only at the Apollo Theater in New York! The Shoddy Mathemagician is world-famous for his shoddy magic tricks like pulling streamers out of his mouth and his specialty, the Disconnected Thumb! Thomas’ll be performing his new magic trick, One Point, One Slope, ONE LINE! The Shoddy Mathemagician claims that, given any one point and any one slope, he’ll be able to tell the audience how many lines run through that point. They say a magician never reveals his secrets, but we’ll clue you into the inner-workings of the Shoddy Mathemagician’s new trick. First, the Shoddy Magician asks the audience for an equation for a line in standard form, ‘y’ equals 'mx' plus ‘b’. The audience responds with 'm' equals 2, and the point (0, 8). If you notice, the point (0, 8) lies on the y-axis. This means that when 'x' is zero, 'y' is equal to 8. We can express the y-intercept of the line from the standard form by setting 'b' equal to 8. Doing this gives us the equation 'y' equals 2x plus 8. Let’s graph what we have so far, so it’s easier to see. We already have our point with the coordinates (0, 8). Since our slope is 2, and because slope is rise over run, we can count to the right one and up two to find the next point on the line. This gives us the point (1, 10). Let's do it again to make sure the points will still be on the same line. One to the right and up two, leaving us with the point (3, 12). After connecting these points, we can see we've drawn a line. How many lines pass through the point (0, 8) with a slope of 2? ...ONE!!! Whenever we’re given one point and one slope, there’s only one line that goes through the point. Pretty cool, huh? The audience is stunned! They want more! But this time, with negative numbers! The audience requests the number of lines that pass through the point (0, -5) with a negative one-half slope. Just like before, notice how our 'x' term is zero. This, of course, means that our y-intercept is negative 5. So we can let 'b' equal negative 5. The audience requested a slope of negative one-half, so 'm' is negative one-half. This gives us the linear equation in standard form of 'y' equals negative one-half 'x' minus 5. Let’s see this on a graph. We'll start with our y-intercept at (0, -5) and, since our ‘m’ value is -1/2, our slope is -1/2. We count to the left two -- since we’re dealing with a negative slope -- and up one, giving us the next point on our line at (-2, -4). What's that? Of COURSE we'll do it again to make sure the points will still be on the same line! Count to the left two and up one, giving us the next point on our line at (-4, -3). Look what happens when we connect these points. How many lines pass through the point (0, -5) with a slope of negative one-half? That’s right!!! ONE!!! You’re getting the hang of it! You’ll be a mathemagician yet! Just like the Shoddy Mathemagician!!! Let’s review. You can select any one point you want, and any one slope, positive or negative. There will always be one line passing through that point with this slope! Let’s see how the show’s going. Hmm...the audience doesn’t sound too happy. I guess it’s curtains for the Shoddy Mathemagician!
One Point, One Slope, One Line exercise
-
Find the equation for the corresponding line given a point and a slope.
HintsThe $y$-intercept for a line always has the form $(0,b)$. The slope, $m$, is always rise over run. The equation for a line in slope intercept form is $y=mx+b$.
Consider a line going through the point $(0,2)$, with a slope of $3$.
- We can use this point and slope to graph the line.
- $(0,2)$ is the $y$-intercept. To graph it, we put a point on the $y$-axis at the $y$-value of $2$.
- The slope of $3$ means a rise of $3$ and a run of $1$. So we go $1$ unit horizontally then $3$ units vertically to graph the next point, $(1,5)$.
- We draw the line through these points to complete our graph as shown.
- The equation for the line is $y=3x+2$.
SolutionHere is a table showing the relationship between the given information, and the graph and equation for each resulting line:
$ \begin{array}{c|c|c|c} \text{point} & y\text{-int.} & \text{slope} & \text{equation}\\ \hline &&&\\ (0,8) & 8 & 2=\frac21 & y=2x+8\\ &&&\\ (0,-5) & -5 & -\frac12 & y=-\frac12 x - 5 \end{array} $
To graph the line $y=2x+8$:
- Graph the $y$-intercept, $(0,8)$.
- Use the slope of $2$ to run $1$ and rise $2$.
- Graph this new point, $(1,10)$.
- Run and rise again to graph $(2,12)$.
- Graph the line through these points.
- Graph the $y$-intercept, $(0,-5)$.
- Use the slope of $-\frac12$ to run $-2$ and rise $1$.
- Graph this new point, $(-2,-4)$.
- Run and rise again to graph $(-4,-3)$.
- Graph the line through these points.
-
Given a point and a slope, graph the resulting line.
HintsThe lines below are given in slope-intercept form. The slope and the $y$-intercept are identified.
$ \begin{array}{c|c|c|c} y=mx+b & m & b & 3 ~\text{points}\\ \hline &&&\\ y=2x+3 & 2=\frac21 & 3 & (0,3)~(1,5)~(2,7)\\ &&&\\ y=-x+6 & -1=-\frac11 & 6 & (0,6)~(1,5)~(2,4) \end{array} $
Given the line $y=x-12$:
- The slope is $1$.
- The rise over run is $\frac11$.
- From a given point, we go $1$ unit horizontally then $1$ unit vertically to get to another point on the line.
Given the point $(0,1)$ and a slope of $5$:
- The equation is $y=5x+1$.
- The points $(0,1)$, $(1,6)$ and $(2,11)$ are on the line.
SolutionWe know the line has a slope of $1$ and goes through the point $(0,2)$. This means:
- The y-intercept is $2$.
- The rise over run is $\frac11$.
- From the y-intercept, we go $1$ unit horizontally and $1$ unit vertically to get to another point on the graph.
- We can repeat that movement to get additional points.
- The points $(0,2)$, $(1,3)$, and $(2,4)$ are on the graph of the line.
-
Write the equation of the resulting line given a point and a slope.
HintsSlope intercept form for a line is $y=mx+b$. The slope is $m$ and the $y$-intercept is $b$.
Here are some examples of points and slopes, and the equations for the resulting lines:
$ \begin{array}{l|l|l} \text{point} & \text{slope} & \text{equation}\\ \hline &&\\ (0,-15) & m=\frac89 & y=(8/9)x-15\\ &&\\ (0,0) & m=-12 & y=-12x\\ &&\\ (0,-\frac12) & m=-\frac18 & y=(-1/8)x-1/2 \end{array} $
Solution$\begin{array}{l|l|l} \text{point} & \text{slope} & \text{equation}\\ \hline &&\\ (0,-15) & m=4 & y=4x-15\\ &&\\ (0,0) & m=\frac12 & y=(1/2)x\\ &&\\ (0,-101) & m=\frac47 & y=(4/7)x-101\\ &&\\ (0,-1) & m=-1 & y=-x-1\\ &&\\ (0,-4) & m=6 & y=6x-4 \end{array}$
-
Determine a line from a given point and slope.
HintsHere are a few examples of points and slopes, and the equations for the resulting lines:
$\begin{array}{l|l|l} \text{point} & \text{slope} & \text{equation}\\ \hline &&\\ (0,0) & m=3 & y=3x\\ &&\\ (0,14) & m=0 & y=14\\ &&\\ (0,12) & m=-\frac17 & y=-\frac17 x + 12\\ \end{array}$
Solution$\begin{array}{l|l|l} \text{point} & \text{slope} & \text{equation}\\ \hline &&\\ (0,\frac12) & m=2 & y=2x+\frac12\\ &&\\ (0,-21) & m=\frac49 & y=\frac49 x -21\\ &&\\ (0,-8) & m=0 & y=-8\\ &&\\ (0,0) & m=0 & y=0\\ &&\\ (0,1) & m=1 & y=x+1\\ \end{array}$
-
Determining which points lie on which lines.
HintsGiven the equation $y=mx+b$:
- The slope is $m$.
- The $y$-intercept is $b$.
- The point $(0,b)$ is on the graph of the line.
Given the line $y=-\frac16 x +10$:
- The $y$-intercept is $10$.
- The point $(0,10)$ is on the line.
- The slope is $-\frac16$.
- The rise is $-1$ and the run is $6$.
- From the point $(0,10)$, we can run $6$ and "rise" $-1$.
- This gives us the point $(6,9)$, which is also on the line.
Suppose we are given the line $y=\frac13 x + 11$ and a point $(3,12)$ which we don't know is on the line or not.
We can substitute the point in for $x$ and $y$ in the equation. If the result is true, the point is on the line.
$\begin{array}{l} 12=\frac13(3)+11\\ 12=1+11\\ 12=12 \end{array} $
That's true, so the point $(3,12)$ is on the graph of the line $y=\frac13 x +11$.
Solution$ \begin{array}{c|c|c|c} y=mx+b & \text{slope} & \text{y-int.} & \text{points}\\ \hline &&&\\ y=2x-7 & 2=\frac21 & -7 & (0,-7)\\ &&&\\ y=7x & 7=\frac71 & 0 & (0,0)\\ &&&\\ y=\frac17 x +7 & \frac17 & 7 & (0,7)\\ &&&\\ y=-\frac17 x + 1 & -\frac17 & 1 & (0,1)~(7,0)\\ &&&\\ y=7x-14 & 7=\frac71 & -14 & (0,-14) \end{array} $
-
Prove that given a slope and point, there's only one line with that slope passing through that point.
HintsPlugging the point $(s,t)$ into $y=mx+b$ gives us $t=ms+b$.
If $t=ms+b_1$ and $t=ms+b_2$ then $ms+b_1=ms+b_2$.
If $ms+b_1=ms+b_2$, then $b_1=b_2$.
SolutionLet’s say that we have two lines, $y=mx+b_1$ and $y=mx+b_2$, with the same slope $m$, and that both of these lines pass through the point $(s,t)$. Then we know that if we plug the point $(s,t)$ into $y=mx+b_1$ and $y=mx+b_2$, then both of our equations will be true. So, plugging $(s,t)$ in, we have that $t=ms+b_1$ and $t=ms+b_2$. Since the left-hand sides of both of these equations are both equal to $t$, we can set them equal to each other to get $ms+b_1=ms+b_2$. Using opposite operations, we subtract $ms$ from both sides of the equation to get $b_1=b_2$. But if $b_1=b_2$, then the two lines, $y=mx+b_1$ and $y=mx+b_2$, must be the same line after all! So, indeed, there is really only one line with slope $m$ which passes through the point $(s,t)$.