The Slope of the Line y=mx+b
- Understanding Slope as a Rate of Change
- Different Types of Slope
- Finding the Slope on a Graph – Step-By-Step Instructions and Examples
- Finding the Slope When Given Two Points – Step-by-Step Instructions
- Finding the Slope from an Equation
- The Slope of a Line – Practice Questions
- The Slope of a Line – Summary
- The Slope of a Line – Frequently Asked Questions

Basics on the topic The Slope of the Line y=mx+b
Slope of a Line – Definition
In everyday life, we encounter slopes from the steepness of a hill to the angle of a ramp. In mathematics, the slope of a line measures how steep a line is.
The slope represents the steepness or incline of a line, defined as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.
Understanding Slope as a Rate of Change
The slope of a line is a measure of how one variable changes in relation to another. It's the same as a rate of change you might encounter in everyday life, such as speed.
For example, imagine you're on a road trip and want to calculate the average speed of your journey. Speed is a rate of change - it reflects how distance changes over time. In this case, the slope (speed) is the change in distance (rise) divided by the change in time (run).
Graphing the Data:
- Plot these points on a graph with 'Time' on the x-axis and 'Distance' on the y-axis.
Finding the Slope (Speed):
- Choose any two points on the graph. For example, (1, 50) and (3, 150).
- Apply the slope formula: Slope (Speed) = ($\dfrac{\text{rise}}{\text{run}}$) = ($\dfrac{\text{Change in Distance}}{\text{Change in Time}}$)
- Slope (Speed) = $\frac{(150 - 50)}{(3 - 1)} = \frac{100}{2} = 50$ miles per hour.
Equation of the Line:
- The equation representing this relationship in the form $y = mx$ could be written as Distance = $50 \times{time}$.
- This equation tells us that for every hour of travel, the distance increases by 50 miles.
Understanding the concept of slope as a unit rate, like speed, helps make connections between mathematical concepts and real-world scenarios. It demonstrates how slope is not just a theoretical idea but a practical tool for everyday calculations.
Different Types of Slope
| Type Of Slope | Description | Graph | Example |
|---|---|---|---|
| Positive Slope | Rises to the right, indicating the slope value is a positive number. As you move from left to right, the line goes up. |  |
$m = \frac{3}{4}$ |
| Negative Slope | Falls to the right, indicating the slope value is a negative number. As you move from left to right, the line goes down. |  |
$m = \frac{-5}{2}$ |
| Zero Slope | Represents a horizontal line, indicating the slope value is zero. There's no rise over the run. |  |
$m = 0$ |
| Undefined Slope | Represents a vertical line, indicating the slope is undefined because division by zero is not possible in mathematics. |  |
Slope is undefined |
Finding the Slope on a Graph – Step-By-Step Instructions and Examples
When looking at a graph, the slope ($m$) is determined by how much the line rises (goes up or down) for every unit it runs (moves right). This can be visually represented and calculated as $m = \frac{\text{rise}}{\text{run}}$.
| Step | Description | Visual |
|---|---|---|
| Identify Points | Locate the points on the graph. For this example, the points are $(1, 1)$ and $(3, 4)$. |  |
| Rise and Run | Observe the rise and run between the points. From $1$ to $4$ is a rise of 3 units (upwards), and from $1$ to $3$ is a run of 2 units (to the right). |  |
| Slope Calculation | Calculate the slope using the rise over run. The slope $m = \frac{3}{2}$, indicating the line rises 3 units for every 2 units it moves to the right. |  |
Find the slope of the graphs.
Finding the Slope When Given Two Points – Step-by-Step Instructions
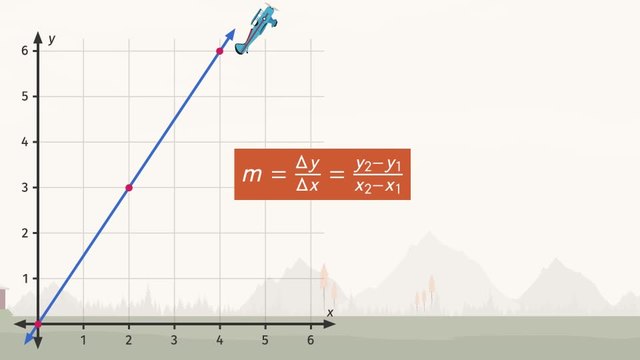
To calculate the slope, use the formula $m = \frac{y_2 - y_1}{x_2 - x_1}$ when you know at least two points on the line. This formula makes it easy to see how steep a line is without a protractor.
What is the slope of the line that passes through the points $(6, -3)$ and $(2, 7)$?
To calculate the slope of a line given two points, $(x_1, y_1)$ and $(x_2, y_2)$, we use the slope formula:
Step 1: Identify the coordinates of the two points.
Point 1: $(6, -3)$, where $x_1 = 6$ and $y_1 = -3$
Point 2: $(2, 7)$, where $x_2 = 2$ and $y_2 = 7$
Step 2: Plug the coordinates into the slope formula.
$m = \frac{7 - (-3)}{2 - 6}$
Step 3: Perform the subtraction in the numerator and the denominator.
$m = \frac{7 + 3}{2 - 6}$
$m = \frac{10}{-4}$
Step 4: Simplify the fraction.
$m = -\frac{5}{2}$
Therefore, the slope of the line passing through the points $(6, -3)$ and $(2, 7)$ is $-\frac{5}{2}$.
This negative slope indicates that the line falls as it moves from left to right.
Try some on your own!
Computing the slope of a line can be useful when analyzing data and identifying patterns.
Finding the Slope from an Equation
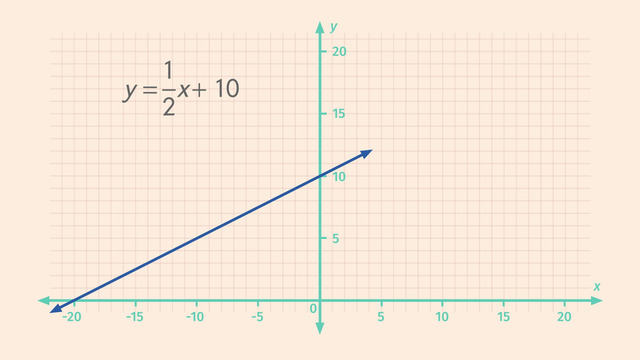
Understanding how to find the slope from an equation involves recognizing the slope-intercept form of a line, which is expressed as $y = mx + b$. In this form, $m$ represents the slope of the line, indicating how steep it is and in which direction it tilts. The $b$ value represents the y-intercept, where the line crosses the y-axis.
The slope-intercept form $y = mx + b$ provides a straightforward way to identify the slope directly from the equation of a line. The coefficient of $x$ (that is, $m$) is the slope. This tells us by how many units $y$ changes for every one-unit increase in $x$.
Consider the equation of a line $y = 2x + 3$.
Identify the Slope: In the equation $y = 2x + 3$, the coefficient of $x$ is $2$. This means the slope ($m$) of the line is $2$.
Interpret the Slope: A slope of $2$ means that for every one unit the $x$ value increases, the $y$ value increases by $2$ units. This indicates the line rises to the right.
The Slope of a Line – Practice Questions
The Slope of a Line – Summary
Key Learnings from this Text:
The slope of a line tells us how steep it is by comparing the vertical change to the horizontal change between two points.
Slope is directly related to the rate of change, similar to everyday concepts like speed. It shows how quickly one thing changes in relation to another.
You can find the slope by using the formula $m = \frac{y_2 - y_1}{x_2 - x_1}$, which helps us understand the line's incline without needing any special tools.
By looking at a graph, we can visually determine the slope by identifying the rise and run between two points. This visual approach makes it easier to understand the concept of slope.
Understanding slope is crucial for solving real-life problems, from designing ramps to calculating how fast an object moves. It's a practical skill that connects classroom math to the world around us.
Having a solid understanding of the slope of a line will be helpful with graphing linear equations, and solving systems of equations by graphing.
The Slope of a Line – Frequently Asked Questions
Transcript The Slope of the Line y=mx+b
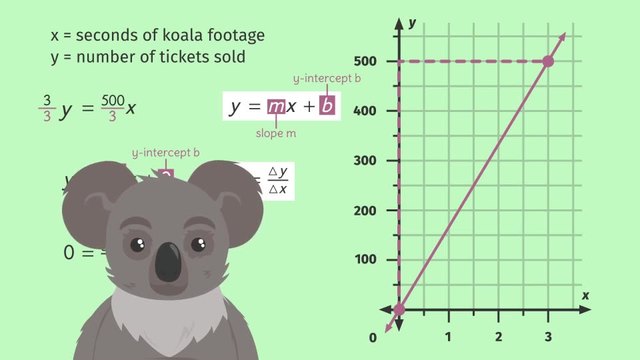
There's trouble on the set of FISTS OF DANGER, the new, big-budget action movie from Furious Films. The movie is missing something...but what? According to the latest research, adding scenes with adorable animals to any movie will increase ticket sales! This may sound like a weird idea for an action film but with some cute animals and the slope of the line y = mx + b, we could save this movie yet! Studies show that for each second of baby koala footage featured in a film, ticket sales go up.
This linear relationship is expressed in the following equation: 3y equals 500x where 'x' represents seconds of koala footage and 'y' is the number of tickets sold. To better understand this equation, let’s rewrite it using slope-intercept form, or 'y equals mx + b'. Using this form, it will be easier for us to understand how 'x' and 'y' change in relation to each other. To get our equation in this form, all we have to do is isolate the variable, 'y'. To get 'y' by itself, we can divide both sides of the equation by 3, thanks to the division property of equality. Great! Now our equation is in slope-intercept form, so we can easily identify the slope, 'm', which will always be the coefficient of 'x'. Here, the slope 'm' equals 500 over 3, or 500 thirds. Remember that slope represents the change in 'y' over the change in 'x'.So that means, for every 3 seconds of footage of baby koalas, we sell 500 more tickets.
Wait, what about the 'b' in our 'y equals mx + b'? The 'b' term tells us the y-intercept, or the value of 'y' when 'x' equals zero. It may not look like it, but our equation actually DOES have a 'b' term. Here, 'b' is just zero. So that means when 'x' is 0, 'y' is also 0, so the graph of this line passes through the origin at (0, 0). To sketch this graph, start with a known point on the line, like (0, 0). Then go up and over according to your slope. Up for change in 'y', over for change in 'x'. Since our slope is 500 over 3, we go up 500 and over 3. Now draw a straight line through the points! Whoa, we've got to get some more baby koalas in on this project!
What other animals can we get on board? Research also shows that having a miniature teacup pig on screen can boost ticket sales. This can be represented by using the equation, 120x minus 4y equals 20 where 'x' represents seconds of pig footage and 'y' is the number of tickets sold. Let's transform this equation into 'y equals mx + b' so we can figure out how the teacup pigs are going to affect ticket sales. To get 'y' alone, subtract 120x from both sides and divide every term in the equation by negative 4, to cancel out the coefficient of 'y'. Finally, we can rearrange the terms on the right side of the equation so it matches the more familiar form of 'y equals mx plus b' that we recognize. Now we can easily identify the slope, 'm', as the coefficient of 'x'. The slope tells us that for every second of teacup pig footage, we sell 30 more tickets. We can also easily identify 'b', or the y-intercept, at (0, -5). To sketch this graph, let's start with the point we just found. Now use what we know about the slope and go up 30, to the right 1, and draw a line through these points. Those pigs have got a future in Hollywood!
But not all animals are so good for the movies. The notorious honey badger has a crippling effect on ticket sales. Let’s take a look at this formula. 3x plus 5y equals 10 where 'x' represents seconds of honey badger footage and 'y' is the number of tickets sold. Let’s isolate the variable, 'y'. Start by subtracting 3x from both sides and divide all the terms in the equation by 5. Much better! The slope in this equation is negative 3 over 5. This means for every 5 seconds of honey badger screen time, the movie actually sells 3 fewer tickets. We can also easily identify the y-intercept, or 'b', at (0, 2). So how do we graph this line? Start with a point you know, like the y-intercept at (0, 2). Because the slope is negative, we then go down 3, to the right 5. Now we draw a line through these points man those badgers are really dragging sales down!
To review: We can write linear equations using the form 'y = mx + b'. This is known as Slope-Intercept Form. In this form, 'm' represents the slope the line, or change in 'y' over change in 'x' and 'b' is the y-intercept, or where the line crosses the y-axis.
Using the market research, the studio executives have gone ahead and reshot their film using a new title... …TROUBLE CUTIES?´Man, Hollywood really has changed these cute little guys...
The Slope of the Line y=mx+b exercise
-
Recall how to write equations in slope-intercept form.
HintsIsolate the variable $y$ to put the linear relationship into slope-intercept form.
Subtract the $x$ term from both sides of the equation.
Divide every term by the coefficient of $y$ to cancel it out.
SolutionAll linear relationships can be written in slope-intercept form, $y=mx+b$, by isolating the variable $y$.
1. For the koala example, the linear relationship is $3y=500x$.
- Divide both sides by $3$.
- $y=\frac{500}{3}x$
- Subtract $120x$ from both sides of the equation.
- $-4y=20-120x$
- Divide all terms by $-4$.
- $y=-5+30x$
- Rearrange the terms on the right.
- $y=30x-5$
- Subtract $3x$ from both sides of the equation.
- $5y=10-3x$
- Divide all terms by 5.
- $y=2-\frac{3}{5}x$
- Rearrange the terms on the right.
- $y=-\frac{3}{5}x+2$
-
Identify the slope and the $y$-intercept of each equation.
HintsSlope-intercept form is $y=mx+b$.
The slope is $m$ and the $y$-intercept is $b$.
To get $y$ alone, subtract the $x$ term if necessary, then divide each term by the coefficient of $y$.
SolutionSlope-intercept form is $y=mx+b$ where $m$ is the slope and $b$ is the $y$-intercept. To find $m$ and $b$, put all of the equations in slope-intercept form $y=mx+b$.
- $y=2x+1$ is in slope-intercept form. Therefore, the slope is $2$ and the $y$-intercept is $1$.
- $y=\frac{8}{5}x$ is in slope-intercept form. Therefore, the slope is $\frac{8}{5}$ and the $y$-intercept is $0$ since there is no $b$ in the equation.
- $y=-\frac{1}{2}x-3$ is in slope-intercept form. Therefore the slope is $-\frac{1}{2}$ and the $y$-intercept is -3.
- $4x+y=1$ is not in slope-intercept form. Subtracting $4x$ from both sides of the equation yields $y=1-4x$. Then, rearrange the terms on the right so the equation is $y=-4x+1$. Now it looks like $y=mx+b$, which means the slope is $-4$ and the $y$-intercept is $1$.
- $-2y=3x-6$ is not in slope-intercept form. To get $y$ alone, divide every term by $-2$: $y=-\frac{3}{2}+3$. The equation is now in the form $y=mx+b$, which means the slope is $-\frac{3}{2}$ and the $y$-intercept is $3$.
-
Match the equations with their slope-intercept form.
HintsIsolate the variable $y$ by subtracting the $x$ term from both sides.
Rearrange the terms or flip the equation to make it look like $y=mx+b$.
Divide every term by the coefficient of $y$.
Solution1. $-2y+3x=8$
- Subtract $3x$ from both sides
- $-2y=8-3x$
- Divide every term by $-2$
- $y=-4+\frac{3}{2}x$
- Rearrange the terms to look like $y=mx+b$
- $y=\frac{3}{2}x-4$
- Subtract $12x$ from both sides
- $3y=6-12x$
- Divide every term by $3$
- $y=2-4x$
- Rearrange the terms on the right
- $y=-4x+2$
- Multiply both sides by $3$
- $y=6x$
- Divide every term by 5
- $y=4x+6$
- Flip the equation
- $3y=9x+8$
- Divide every term by $3$
- $y=3x+\frac{8}{3}$
- Flip the equation
- $6y=4x$
- Divide both sides by $6$ and simplify
- $y=\frac{2}{3}$
-
Graph the equation $-y-3x+4=0$.
HintsThe graph of a line is $y=mx+b$, where $m$ is the slope and $b$ is the $y$-intercept.
To graph the $y$-intercept, plug $x=0$ into the equation.
The slope, $m$, is the change in $y$ divided by the change in $x$.
SolutionThe line $-y-3x+4=0$ can be rewritten in slope-intercept form by solving for $y$.
$~$
To solve for $y$:
1. Add $3x$ to both sides: $-y+4=3x$.
2. Subtract $4$ from both sides: $-y=3x-4$.
3. Divide both sides by $-1$: $y=-3x+4$.
$~$
To identify the slope and $y$-intercept:
- The slope is $m=-3$.
- The $y$-intercept is $b=4$.
To identify the point at $x=1$:
- Start at the $y$-intercept, $(0,4)$.
- As the slope is $m=-3$, if we subtract $3$ from the $y$-coordinate and add $1$ to the $x$-coordinate of a point on our line, we get another point on our line.
- Doing this with our $y$-intercept, we get $(0+1,4-3)=(1,1)$, which is the point on our line at $x=1$.
- Use the slope $m=-3$ to find the point at $x=1$.
To graph:
1. Plot the $y$-intercept $(0,4)$.
2. Plot the point $(1,1)$.
3. Draw a line connecting these two points.
-
Determine if the equation is written in slope-intercept form or not.
HintsSlope-intercept form is $y=mx+b$.
Slope-intercept form can also look like $y=b+mx$, $mx+b=y$ or $b+mx=y$.
If there is no $y$-intercept $b$, slope-intercept form will look like $y=mx$.
SolutionSlope-intercept form is $y=mx+b$. However, the terms can be rearranged and still be in slope-intercept form. The following equations are $4$ different ways to represent slope-intercept form.
- $y=mx+b$: the original slope-intercept form
- $y=b+mx$: the terms on the right side are switched
- $mx+b=y$: the equation is flipped so that y is on the right
- $b+mx=y$: the equation is flipped with y on the right, and the $mx$ and $b$ terms are switched
The following equations are in slope-intercept form because they match one of the equations listed above.
- $y=5x-3$
- $y=4+2x$
- $y=-\frac{2}{5}x$
- $y=-4x$
- $1-3x=y$
- $-x+1=y$
- $x=-\frac{1}{2}y+1$
- $\frac{3}{2}x+y=2$
- $2y=x+1$
- $x=-\frac{1}{2}y+1$
- $-y=2x-3$
- $7y=2x$
-
Determine the line.
HintsSlope-intercept form is $y=mx+b$, where $m$ is the slope and $b$ is the $y$-intercept.
If $x=0$ in the point $(x,y)$, then the $y$-coordinate is the $y$-intercept $b$.
If $x\neq 0$ in the point $(x,y)$, substitute the slope $m$ and the point $(x,y)$ into $y=mx+b$, and solve for $b$.
SolutionSlope-intercept form, $y=mx+b$, consists of a point $(x,y)$, a slope $m$, and a $y$-intercept $b$. Given a point and a slope you can uniquely determine a line.
1. $(0,-4)$, $m=\frac{1}{2}$
- Since $x=0$, we know that the $y$-intercept is $-4$, $b=-4$
- Now we can substitute $m$ and $b$ into $y=mx+b$
- $y=\frac{1}{2}x-4$
- Since $x=0$, we know that the $y$-intercept is $\frac{35}{2}$, $b=\frac{35}{2}$
- Now we can substitute $m$ and $b$ into $y=mx+b$
- $y=\frac{3}{5}x+\frac{35}{2}$
- Since $x\neq 0$, we substitute the values of $x$, $y$, and $m$ into $y=mx+b$, to solve for $b$.
- $2=2(1)+b$
- $2=2+b$
- $0=b$
- Now that we know $b=0$, we can substitute $b$ and $m$ into $y=mx+b$
- $y=2x+0$
- $y=2x$
- Since $x\neq 0$, we substitute the values of $x$, $y$, and $m$ into $y=mx+b$, to solve for $b$.
- $-3=-2(-1)+b$
- $-3=2+b$
- $-5=b$
- Now that we know $b=-5$, we can substitute $b$ and $m$ into $y=mx+b$
- $y=-2x-5$
- Since $x=0$, we know that the $y$-intercept is $-6$, $b=-6$
- Now we can substitute $m$ and $b$ into $y=mx+b$
- $y=-\frac{17}{3}x-6$
- Since $x\neq 0$, we substitute the values of $x$, $y$, and $m$ into $y=mx+b$, to solve for $b$.
- $4=6(4)+b$
- $4=24+b$
- $-20=b$
- Now that we know $b=-20$, we can substitute $b$ and $m$ into $y=mx+b$
- $y=6x-20$
- Since $x\neq 0$, we substitute the values of $x$, $y$, and $m$ into $y=mx+b$, to solve for $b$.
- $3=\frac{1}{4}(-4)+b$
- $3= -1+b$
- $4=b$
- Now that we know $b=4$, we can substitute $b$ and $m$ into $y=mx+b$
- $y=\frac{1}{4}x+4$









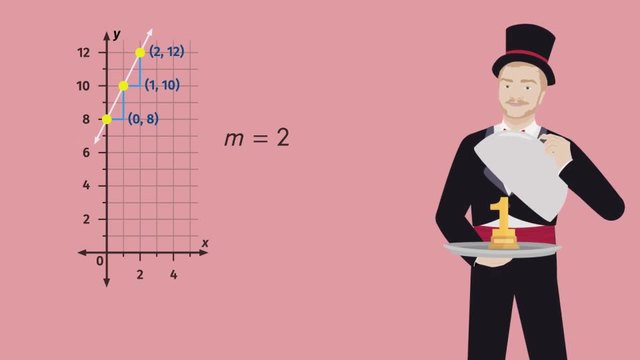











this website changed my life