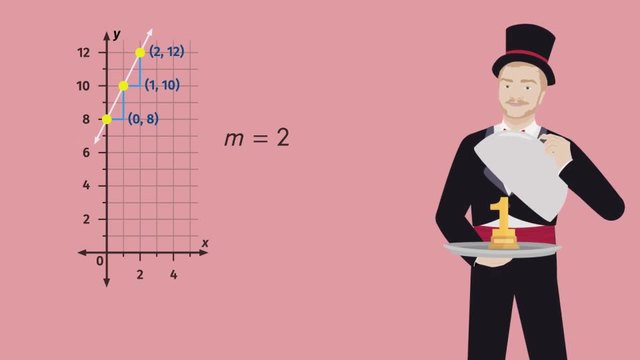What is the slope m?
Learning text on the topic What is the slope m?
What is Slope?
Have you ever walked up a steep incline or driven down a gentle hill? The concept of slope reflects similar ideas but in the realm of mathematics, specifically in algebra and geometry.
Slope is a fundamental idea in mathematics, describing the rate at which a line ascends or descends in a coordinate plane. It is represented by the variable "m", which is believed to stand for monter, the French verb for "to climb," although this is more anecdotal than definitive.
Mathematically, the slope is the ratio of the change in the y-coordinate (rise) to the change in the x-coordinate (run) as you move from one point to another along a line.
Different Types of Slope
| Slope Type | Description | Characteristics |
|---|---|---|
| Positive | The line rises from left to right. | As $x$ increases, $y$ also increases. |
| Negative | The line falls from left to right. | As $x$ increases, $y$ decreases. |
| Zero | The line is horizontal. | No change in $y$ as $x$ increases. |
| Undefined | The line is vertical. | No change in $x$ as $y$ increases or decreases. |
Slope-Intercept Form
The slope is commonly introduced as part of the slope-intercept form of a linear equation: y = mx + b.
| Symbol | Description | Role in Equation |
|---|---|---|
| $ m $ | Slope of the line | Measures the steepness and direction of the line. |
| $ x $ | Independent variable (horizontal axis) | Determines the value along the x-axis for each point on the line. |
| $ b $ | Y-intercept | The point where the line crosses the y-axis. |
| $ y $ | Dependent variable (vertical axis) | Calculated from the equation, representing the value along the y-axis. |
How to Find the Slope
There are various methods to determine the slope of a line depending on the available information. You might have a graph, an equation, or two coordinates from which to calculate the slope. The slope, often denoted as $ m $, is a measure of how steep a line is, and it's calculated as the ratio of the rise (change in $ y $) over the run (change in $ x $).
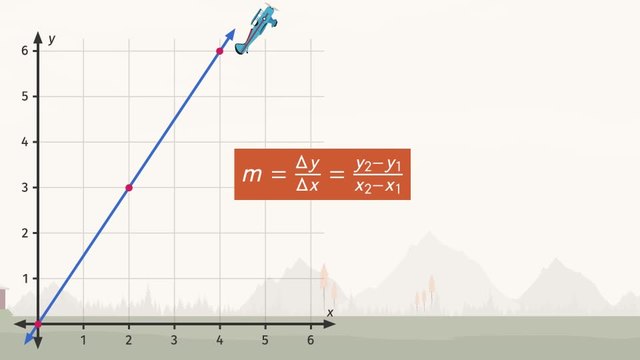
Finding the Slope from a Graph
To find the slope from a graph:
- Identify two points on the line $ (x_1, y_1) $ and $ (x_2, y_2) $.
- Determine the rise: The change in $ y $ (vertical change) between the two points.
- Determine the run: The change in $ x $ (horizontal change) between the two points.
- Calculate the slope as $ m = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1} $.
Example: Suppose you are given two points on a graph, $ (1, 2) $ and $ (3, 6) $.
- Identify the points: $ (x_1, y_1) = (1, 2) $ and $ (x_2, y_2) = (3, 6) $.
- Determine the rise: $ 6 - 2 = 4 $.
- Determine the run: $ 3 - 1 = 2 $.
- Calculate the slope: $ m = \frac{4}{2} = 2 $.
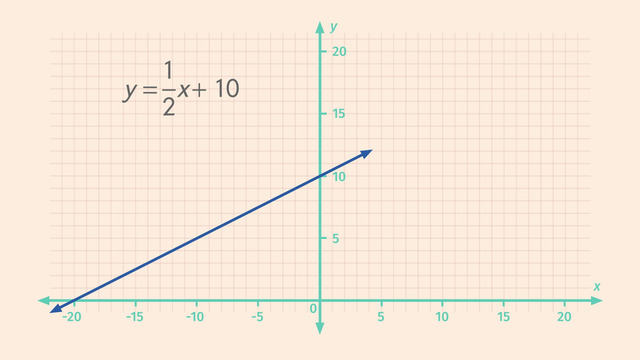
Finding the Slope given an Equation
If the equation of the line is given in the slope-intercept form, $ y = mx + b $, the slope $ m $ can be directly identified as the coefficient of $ x $.
Example: Consider the equation $ y = \frac{5}{3}x - 7 $.
- Identify the coefficient of $ x $, which is $ \frac{5}{3} $.
- State the slope: The slope $ m $ is $ \frac{5}{3} $.
Finding the Slope given Two Points
When given two points, the formula for the slope is $ m = \frac{y_2 - y_1}{x_2 - x_1} $.
Example: For points $ (5, 11) $ and $ (1, 3) $:
- Subtract the $ y $-coordinates: $ 11 - 3 = 8 $.
- Subtract the $ x $-coordinates: $ 5 - 1 = 4 $.
- Calculate the slope: $ m = \frac{8}{4} = 2 $.
What is Slope? – Practice
Practice working with slope on your own.
Why is Slope "m"? – Summary
Key Learnings from this Text:
- Slope (m) represents the steepness or incline of a line, defined as the ratio of the vertical change (rise) to the horizontal change (run) between two points on a line.
- The slope-intercept form of a linear equation is y = mx + b, where "m" is the slope and "b" is the y-intercept.
- To determine the slope between two points, use the formula: m = (y2 - y1) / (x2 - x1).
- The importance of slope lies in its representation of the rate of change, which can have real-world applications like calculating speed or growth rates.
- The x-intercept is affected by the slope; a steeper slope means the line will cross the x-axis sooner.
- Other related terms such as y-intercept, coordinate plane, and graph are important for understanding the complete picture of linear equations and their slopes.
Remember, mastering the concept of slope will significantly aid in solving and graphing linear equations. For more in-depth practice and interactive content, explore other resources on our educational platform that can further support your learning journey in algebra.
Why is Slope "m"? – Frequently Asked Questions
