Introduction to Absolute Value
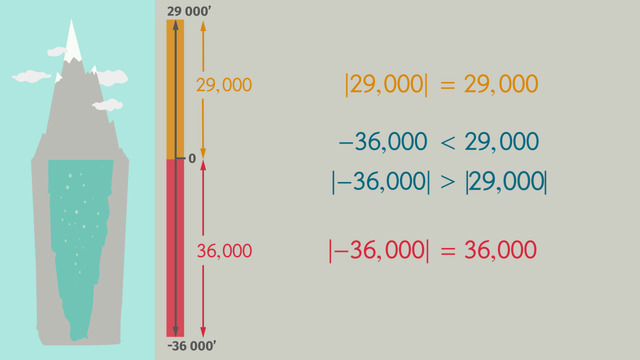

Basics on the topic Introduction to Absolute Value
The absolute value of a number is its distance from zero. Another way of thinking of absolute value is it’s the magnitude of a number – without consideration of its sign.
So for a negative number, just drop the sign, and that’s the absolute value; for a positive number, the absolute value is the number. We can conclude the absolute value of a number is always a positive number. What about zero? The absolute value of zero is zero.
To help you understand absolute value, model problems using a vertical or horizontal number line. With help from the number line, the difference from zero and the absolute value of the difference between numbers will be quite obvious.
The symbol for absolute value is a vertical line on either side of the quantity, albeit number or variable. We can credit mathematician Karl Weierstrass with thinking up the symbol for absolute value.
How can we use this concept in the real world? There are many applications, but just to name a few: distance, weights and measures, and temperature. If your friend tells you there is a great record store just 4 blocks away, it might be helpful to understand that your friend is telling you the absolute value of the number of blocks, so you’ll know to ask which direction before you go off on a wild goose chase. I don’t know if you’ll ever find the record store, but I absolutely recommend that you watch this video.
Represent and solve equations with absolute value.
CCSS.MATH.CONTENT.HSA.REI.D.11
Transcript Introduction to Absolute Value
Phillip and Lara are saying hello from the Netherlands, where the topography is very flat. Most of the land is barely above sea level!
Since they're having so much fun on their vacation, Phillip and Lara are already thinking about where to go for their next trip. Lara loves to climb mountains, but Phillip loves to scuba dive.
Phillip and Lara might not agree on what to do, but they do agree on where to go. They both want to get as far away from sea level as possible. Wherever that place is, that's where they'll go.
Lara suggests Mount Everest, the point with the highest altitude on Earth, with an elevation of 29,000 feet above sea level. Phillip proposes a trip to visit the Mariana Trench, the deepest place on Earth, around negative 36,000 feet, or 36,000 feet below sea level. Let’s analyze the facts and help Phillip and Lara decide where to go on their next trip.
What is Absolute Value?
We know negative numbers are less than positive numbers. So, negative 36,000 feet, the depth of the Mariana Trench, is less than the elevation of Mount Everest, which reaches a height of 29,000 feet. So does that mean Mount Everest is the place to go?
Not necessarily. To solve this problem, we need to know the absolute value of the height and depth of each location. The absolute value of a number is the number's distance from zero, regardless of whether the number is positive or negative.
Absolute Value Example
- A depth of negative 36,000 feet is 36,000 feet from sea level. So the absolute value of negative 36,000 is 36,000.
- A height of 29,000 feet is 29,000 feet from sea level. So the absolute value of 29,000 is 29,000. Absolute values are always positive numbers. Always!
- The absolute value of negative 36,000 is greater than the absolute value of 29,000 because 36,000 is greater than 29,000.
So he lowest point of the Mariana Trench is farther from sea level than is Mount Everest's peak. We have a winner!
Before Phillip and Lara pack up their scuba gear and suntan lotion, let’s summarize the facts:
- The absolute value of a positive number is simply equal to the number.
- The absolute value of a negative number is equal to the opposite of that number, which is always positive, and the absolute value of zero is zero.
More Examples
Let's look at a few more situations:
- What's the negative of the absolute value of a positive number? It's a negative number.
- What's the negative of the absolute value of a negative number? A negative number also.
- What if there's an expression inside the absolute value bars? You must simplify the expression first then determine the absolute value. If the expression is a big one, remember to use PEMDAS.
In the Mariana Trench, Phillip is having the time of his life scuba diving in very deep water, but what about Lara?
How about that? She found a mountain to climb, after all. Uh oh. I don't think that's a mountain.
Introduction to Absolute Value exercise
-
Describe absolute value.
HintsNote
$|x| = \begin{cases} x& \text{if }x>0 \\ -x& \text{if }x<0\\ 0& \text{if }x=0 \end{cases}$
Negative numbers are smaller than positive numbers.
Absolute values are always positive numbers.
SolutionAs far away from sea level as possible:
- could be an elevation such as the peak of Mount Everest, or
- could as well the deepest point of the Mariana Trench.
- it's about 29000 feet to the peak of Mount Everest and
- about -36000 feet to the deepest point of the Mariana Trench.
But, to determine the distance from sea level, we have to look at the absolute values:
- $|29000|=29000$ and
- $|-36000|=36000$.
We get the largest distance from sea level:
$36000>29000$.
Therefore, Lara and Philip will spend their next holiday in the Mariana Trench.
-
Determine the absolute value of the numbers.
HintsNote
$|x| = \begin{cases} x& \text{if }x>0 \\ -x& \text{if }x<0\\ 0& \text{if }x=0 \end{cases}$
The absolute value is always positive. So, the negative of an absolute value is always negative.
Working with more complicated expressions: First, solve the expression that is between the absolute value bars, and then find the absolute value of the simplified expression.
SolutionThe absolute value of a positive number is simply equal to the number: $|3|=3$.
The absolute value of a negative number is equal to the opposite of that number and is always positive: $|-5|=5$.
The absolute value of zero is zero: $|0|=0$.
What is the negative of an absolute value?
- $-|3|=-(3)=-3$ as well as
- $-|-5|=-(5)=-5$
And to solve more complicated expressions, simplify the expression within the bars first then find the absolute value of the simplified expression:
- $|3+(-5)|$: We have to calculate $|3+(-5)|=|3-5|=|-2|=2$.
- $|2\times 3+(-5)|=|6+(-5)|=|6-5|=|1|=1$.
-
Determine the winner of the absolute value game.
HintsThe absolute value of a positive number is the number itself: $|32|=32$.
The absolute value of a negative number is the opposite of the number: $|-64|=64$.
The absolute value of zero is zero: $|0|=|0|$.
If you have to determine the absolute value of a more complicated expression, first simplify the expression.
Use the Distributive Property:
$a\times(b+c)=a\times b+ a\times c$.
SolutionThe absolute value of a positive number is the number itself: $|32|=32$. The absolute value of a negative number is the opposite of the number $|-64|=64$. The absolute value of zero is zero: $|0|=|0|$.
If we have to determine the absolute value of a more complicated expression, first simplify the expression.
For each of the following examples, we will determine the the absolute value. Afterwards we 'll be able to decide who wins the game.
- $|-23|=23$ and $|46|=46$. So $|-23|<|46|$. Philip wins.
- $|-46|=46$ and $|23|=23$. So $|-46|>|23|$. Lara wins.
- $|-23|=23$ as well as $|23|=23$. So $|-23|=|23|$. Draw.
- $|46|46$ as well as $|-46|=46$. So $|46|=|-46|$. Draw.
- $|23+46|=|69|=69$ and $|23-46|=|-23|=23$. So $|23+46|>|23-46|$. Lara wins.
- $|-23-46|=|-69|=69$ and $|46-23|=|23|=23$. So $|-23-46|>|46-23|$. Lara wins.
- $|-23+46\times2|=|-23+92|=|69|=69$ and $|3\times (-23)|=|-69|=69$. So $|-23+46\times2|=|3\times (-23)|$. Draw.
- $|2\times(-23+46)|=|2\times(-23)|=|-46|=46$ and $|2|\times(|-23|+|46|)=2\times(23+46)=2\times 69=138$. So $|2\times(-23+46)|<|2|\times(|-23|+|46|)$. Philip wins.
-
Decide which terms have the same absolute value.
HintsThe absolute value of a positive number is simply equal to the number.
The absolute value of a negative number is the opposite of the number.
First, determine the value of the expression between the absolute value bars.
For example:
$|2\times(-2+3)|=|2\times 1|=|2|=2$.
SolutionHere is cheat sheet for absolute value:
$|x| = \begin{cases} x& \text{if }x>0 \\ -x& \text{if }x<0\\ 0& \text{if }x=0 \end{cases}$
Here we have different expressions using absolute value:
- $|-6+9|=|3|=3$
- $|6|-|-9|=6-9=-3$
- $-|9-6|=-|3|=-3$
- $|-9+6|=|-3|=3$
- $|-9|-|-6|=9-6=3$
- $-|-9|+|-6|=-9+6=-3$
-
Decide which is further from sea level.
HintsFor example $|-3|=3$ as well as $|3|=3$.
The absolute value on a number line is the distance of any number to the zero point.
Look at the following example:
- $-6<4$, but
- $|-6|=6>4$.
SolutionLet's have a look at the information we're given:
- From sea level, it's about 29000 feet to the peak of Mount Everest and
- about -36000 feet to the deepest point of the Mariana Trench.
- $|29000|=29000$ and
- $|-36000|=36000$.
$36000>29000$.
So that's the decision: They will go to the Mariana Trench.
-
Find the absolute values.
HintsThe number of steps is always positive while the position on the number line can be negative.
For example: On this number line you can see two steps to the left, the red arrow, and one to the right, the blue arrow.
The position is $-1$ and the number of steps is $|-2|+|1|=2+1=3$.
Four steps to the left gives us
- the position $-4$ and
- $|-4|=4$ steps.
SolutionThe number line on the right shows
- Susan taking three steps to the left and then another step to the left.
- The resulting position is $-4$ and
- the number of steps is $|-3|+|-1|=3+1=4$.
- Seven steps to the right give us the position $7$ and five steps to the left the position $2$. The number of steps can be determined by $|7|+|-5|=7+5=12$.
- Eight steps to the left give us the position $-8$ and twelve steps to the right the position $4$. The number of steps can be determined by $|-8|+|12|=8+12=20$.














Informative, but unrealistic. Both of those situations are far more lethal than the video suggests.
great video helps a lot.