Exponents and Multiplication – Product of Powers Property


Basics on the topic Exponents and Multiplication – Product of Powers Property
If you are solving exponent multiplication problems by writing out equations in the long form, probably your fingers are cramping and you are using lots and lots of paper and sharpening your pencil again and again.
To learn how to save your fingers and some trees, watch this video. Rather than writing out exponent multiplication problems in the long form, use the Product of Powers Rule to make problems easier to solve and finish the work more quickly.
The Product of Powers Rule states: for same base exponents, add the exponents, and then simplify. So, for the problem 2 raised to the 20th power times 2 raised to the 10th power – rather than writing out all of those 2s - since the bases are the same, you can just add the exponents. The answer is 2 raised to the 30th power. Wow that was really fast and no trees had to die!
Now that you can finish your exponent multiplication homework so quickly, what can you do with all the time you will have left? Well since your fingers will no longer be cramped, you can take up knitting while you watch more Algebra I videos from sofatutor. Whatever you decide to do, have fun while learning, and you may be surprised how much fun it is to solve math problems!
Interpret the structure of expressions.
CCSS.MATH.CONTENT.HSA.SSE.A.1
Transcript Exponents and Multiplication – Product of Powers Property
While Ethan chills on the couch, he chats with a friend. Oh no! Let’s take a look at the assignment and see what Ethan needs to do… He needs to write an essay for his English class. Ethan's English teacher, who's also a math enthusiast, gave the students 10² days to write 10³ words EACH DAY about courage. Ethan doesn't think it's so bad. Is he right?
Exponents and multiplication
Using exponents and multiplication, let’s help Ethan figure out how many words he needs to write per day. To make your life easier when multiplying exponents, you can use the Product of Powers rule. When you have a number raised to a power, as in aⁿ, multiplied by another number with the same base, aᵐ, you can write it in long form as 'a' multiplied 'n' times multiplied by 'a' multiplied 'm' times. All together, we can write this product as 'a' multiplied 'n' plus 'm' times.
Add and simplify
Or simply, aⁿ⁺ᵐ. To multiply exponents with the same base, add the exponents, then simplify. So… to calculate the number of words Ethan needs to write in two days, multiply the number of days the teacher assigned to write the essay times the number of words Ethan has to write. (10²)(10³) If you want, you can write out all the tens in long form as we showed you before.
The product of Powers rule
As you can see the 10 is multiplied 2 + 3 times, or simplified 5 times. We can write this as 10⁵.... or you can use the Product of Powers rule and just add the exponents since the base is the same for the numbers we want to multiply. Either way, the answer is 10⁵...or 100,000 words.That’s words, not characters.
Uh oh, that’s way more than Ethan expected. When he got the assignment, the word count seemed small. Feeling a bit dejected, he starts to write. After several hours, he realizes that he can write 1,024 or 2¹⁰ words per hour, and so far, he's written about 25,000 words. He still has 2⁴, or 16, hours to go. Will he get to 100,000 words in time? To solve this, calculate (2⁴)(2¹⁰). You can list the 2s in long form and then multiply, if it helps.
Same bases
As you can see, the 2 is multiplied 10 + 4, or simply, 14 times. You can write this as 2¹⁴...or since the bases are the same, you can use the Product of Powers rule again. (2¹⁰)(2⁴) = 2¹⁴...and that's equal to 16,384 words. We can also write this as 1.6384E4. E4? You might be wondering, what the heck is E4? It's shorthand for 10⁴. Now Ethan understands how to use the Product of Powers rule, but that doesn’t solve his problem...
Solve the problem
With the time he has left to write, he will have about 40,000 words altogether. Oh no! He'll be short 60,000 words, but Ethan has an idea – it’s a power move for sure…Will it work? Probably it won’t, but who knows? Maybe..., just maybe...
Exponents and Multiplication – Product of Powers Property exercise
-
Find out the number of words Ethan has to write by using the Product of Powers Rule.
HintsA power can also be represented with multiplication.
For example, ${\large 2^4=2\times 2\times 2\times 2}$. So the base, ${\large 2}$, is written out as four factors that are multiplied.
${\large \begin{array}{rcl} a^n\times a^m&=&\underbrace{a\times\dots\times a}_{n\text{ times}}\times\underbrace{a\times\dots\times a}_{m\text{ times}}\\ &=&\underbrace{a\times\dots\times a}_{n+m\text{ times}}\\ &=&a^{n+m} \end{array}}$
If you have $10$ to any positive power, write it as $1$ with as many zeros following as the exponent shows.
SolutionWhen Ethan got the message from his teacher, he thought that $10^3$ words per day for $10^2$ days would be completely doable. Poor Ethan.
We have to multiply $10^3$ by $10^2$ to determine the total number of words.
- $10^3$ stands for $10\times 10\times 10$.
- $10^2$ stands for $10\times 10$.
- $10^3\times 10^2=10\times 10\times 10\times 10\times 10$.
This gives us $10^3\times 10^2=10^{3+2}=10^5=100,000$.
Ethan has to write $100,000$ words...like we said...poor Ethan.
-
Determine how many words Ethan will be able to write in the next $16$ hours.
Hints${\Large \begin{array}{rcl} a^n\times a^m&=&\underbrace{a\times\dots\times a}_{n\text{ times}}\times\underbrace{a\times\dots\times a}_{m\text{ times}}\\ &=&\underbrace{a\times\dots\times a}_{n+m\text{ times}}\\ &=&a^{n+m} \end{array}}$
SolutionAll we have to do here to multiply the two numbers, $2^{10}$ and $2^4$, is add the exponents:
$2^{10}\times 2^4=2^{14}$
$2^{14}$, or multiplying $2$ by itself fourteen times, is equal to $16,384$ words. This is the total number of words Ethan can write in $16$ hours.
-
Using the Product of Powers Property, identify the base-exponent pair(s) that are factors of the displayed base-exponent.
Hints$a=a^1$ for any base $a$.
To use the Product of Powers Rule, the bases must be the same, but the exponents can differ.
SolutionWe can only use the Product of Powers Property for exponents with the same base.
$\begin{array}{rcl} a^n\times a^m&=&\underbrace{a\times\dots\times a}_{n\text{ times}}\times\underbrace{a\times\dots\times a}_{m\text{ times}}\\ &=&\underbrace{a\times\dots\times a}_{n+m\text{ times}}\\ &=&a^{n+m} \end{array}$
It doesn't matter if the exponents differ.
So we can simplify as follows:
- ${\large x^2\times x^3=x^{2+3}=x^5}$
- ${\large x\times x^3=x^{1+3}=x^4}$
- ${\large x^5\times x^3=x^{5+3}=x^8}$
- ${\large 2^2\times 2^{16}=2^{2+16}=2^{18}}$
- ${\large 2^3\times 2^{16}=2^{3+16}=2^{19}}$
- ${\large 2^7\times 2^{16}=2^{7+16}=2^{23}}$
- ${\large 2\times 2^{16}=2^{1+16}=2^{17}}$
- ${\large 3^2\times 3^2=3^{2+2}=3^4}$
- ${\large 3^3\times 3^2=3^{3+2}=3^5}$
- ${\large 3^5\times 3^2=3^{5+2}=3^7}$
-
Find out how many animals Ethan has seen by using the Product of Powers Property.
Hints${\large 2=2^1}$
How do you multiply two powers with the same base?
SolutionHere we have always the same base, $2$.
We can apply the Product of Powers Property by adding the exponents of numbers with the same base to figure out the number of animals Ethan has seen sitting by the lake.
Ducks
$\large {2^2\times 2^2=2^{2+2}=2^4=16}$
Ethan has seen $16$ ducks.
Frogs
$\large {2\times 2^4=2^1\times 2^4=2^{1+4}=2^5=32}$
Ethan has also seen $32$ frogs.
Fish
$\large {2^2\times 2^5=2^{2+5}=2^7=128}$
There are $128$ fish in the lake.
Swans
$\large {2^2\times 2=2^2\times 2^1=2^{2+1}=2^3=8}$
$8$ swans passed by Ethan while he was relaxing.
-
Describe how to multiply powers with the same base according to the Power of Products Property.
HintsYou can write each power as a product.
Here is an example for the rule.
SolutionWe've illustrated the Product of Powers Property below. You can use this property when multiplying numbers with the same base raised to an exponent.
${\large \begin{array}{rcl} a^n\times a^m&=&\underbrace{a\times\dots\times a}_{n\text{ times}}\times\underbrace{a\times\dots\times a}_{m\text{ times}}\\ &=&\underbrace{a\times\dots\times a}_{n+m\text{ times}}\\ &=&a^{n+m} \end{array}}$
We can only apply this rule if we have two powers with the same base, for example $\large {a}$.
You multiply two powers with the same base, $\large {a^n}$ and $\large {a^m}$, by adding the exponents $\large {a^{n+m}}$, while keeping the base the same.
$~$
Let's check this with a few examples:
- $\large {2^2\times 2^3=(2\times 2)\times(2\times2\times2)=2^{2+3}=2^5}$
- $\large {4^3\times 4^1=(4\times 4\times 4)\times(4)=4^{3+1}=4^4}$
- $\large {5^2\times 5^4=(5\times 5)\times(5\times5\times5\times5)=5^{2+4}=5^6}$
-
Simplify the given products of powers by using the Product of Powers Property.
HintsIf you have more than two factors, you can generalize the rule:
${\Large \begin{array}{rcl} 4^3\times 4^2\times 4^5&=&4^{3+2}\times 4^5\\ &=&4^5\times 4^5\\ &=&4^{5+5}\\ &=&4^{10}\\ &=&4^{3+2+5} \end{array}}$
${\Large a^n\times a^m=a^{n+m}}$.
${\Large a=a^1}$
SolutionUsing the Product of Powers Rule, we can simplify the multiplication of powers with the same base.
If we have more than one factor, we can still apply the rule: $\large a^n\times a^m\times a^k=a^{n+m+k}$.
When applying the Product of Powers Property, we get:
- ${\large 3^5\times 3\times 3^2=3^{5+1+2}=3^8}$
- ${\large 2^{16}\times 2^4=2^{16+4}=2^{20}}$
- ${\large 10^3\times 10^2\times 10^4\times 10=10^{3+2+4+1}=10^{10}}$
- ${\large 5^5\times 5^5\times 5^5\times 5^5=5^{5+5+5+5}=5^{20}}$


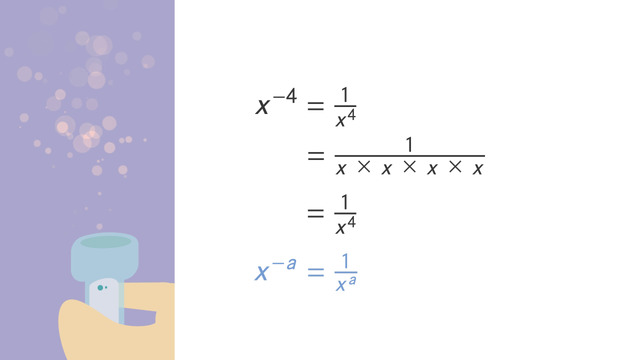













love the texting…relatable☺️