Exponents and Division – the Quotient of Powers Property


Basics on the topic Exponents and Division – the Quotient of Powers Property
The Quotient Property (Quotient of Powers Property, Quotient of Powers Rule) states that we can divide two powers with the same base by simply subtracting their exponents and retaining their common base. For example, dividing the algebraic expression y18 by y12 will give us a result equal to y18-12, or y6, where y can stand for any numerical value except 0; remember that the Quotient Property is only applicable if the expressions share a common base and that base must not be equal to zero. The base cannot be zero because it is not defined by the properties of arithmetic: if 12 could be divided by 0, for instance, then this would mean that the equation 0 times y = 12 would have a solution… which is not possible!
The Quotient Property works because if we do it the “long” way by expanding each expression, y18 = y•y•y•y•y•y•y•y•y•y•y•y•y•y•y•y•y•y and y12 = y•y•y•y•y•y•y•y•y•y•y•y, and then divide, we can see that the 12 y’s in the denominator will cancel out with 12 of the y’s in the numerator, leaving only 6 "y"s remaining in the numerator and no y’s (or the number 1) in the denominator.
We can now calculate, for instance, 225 / 215 = 225-15 = 210, or 1024, and that 0101 / 083 just does not make any sense.
The Quotient Property is very useful in simplifying complicated expressions and makes manipulation of large quantities less tedious and less time-consuming.
Know and apply the properties of integer exponents to generate equivalent numerical expressions. CCSS.MATH.CONTENT.8.EE.A.1
Transcript Exponents and Division – the Quotient of Powers Property
In the year 8008, data is the new money. The more you have, the more you control. We’re at the Schmoogle Headquarters at the lead data trader’s desk, model number AA-RN0, but everyone calls him Arn0. He seems really busy at his job as a data trader. Let’s take a closer look at what he’s working on.
He's talking to his head of engineering, Smicha, who needs to calculate the number of hard drives he needs in order to store all the data on the internet. AA-RN0 is making plans to backup the entire Internet, which is 10²⁵ brontobytes, to become the richest robot in the universe.
But Smicha only has 10¹⁵ brontobytes of space on each of his hard drives.
AA-RN0 has a problem. His calculator doesn’t show enough digits for an accurate calculation. Not knowing what to do, AA-RN0 asks Smicha if he has any ideas. Smicha knows a method to deal with really large numbers and thinks that his knowledge of dividing exponents might come in handy.
Division of Exponents
Smicha shows AA-RN0 that aᵐ / aⁿ = a⁽ᵐ⁻ⁿ⁾, but he warns AA-RN0 that the bases of both numbers have to be the same. Smicha shows AA-RN0 a quick example with numbers instead of letters to help him understand Exponents and Division.
2⁵ / 2³ = 2⁽⁵⁻³⁾ = 2². As you know, this is the same as 32 / 8, which is 4, the same answer we just got. AA-RN0 gives the calculation another try. If the internet has 10²⁵ brontobytes of space, and each of their Gen1 hard drives can hold 10¹⁵ brontobytes of space, AA-RN0 notices that his base is 10, so he writes that down. He then writes 10²⁵ / 10¹⁵ and knows that this equals 10⁽²⁵⁻¹⁵⁾ which is the same as 10¹⁰. Smicha tells AA-RN0 that they need 10¹⁰ hard drives to store all the data.
TEN BILLION ROBOTS!?!? THEY'LL NEVER FINISH!!!
Good news! Smicha just received the Beta model for the Gen2 hard drive. The new Gen2 hard drives can each hold 10¹⁸ brontobytes of data. Smicha now needs to know how many Gen2 hard drives he’ll need to store all the internet’s data. He writes 10²⁵ / 10¹⁸. Following the steps Smicha outlined for him earlier, AA-RN0 rewrites the division expression as 10⁽²⁵⁻¹⁸⁾, which gives him 10⁷ hard drives. They only need to produce 10 million hard drives! They'll be done in a jiffy!
Summary
In order to remember the steps for Exponents and Division, Smicha saves the equation in his memory. aᵐ / aⁿ = a⁽ᵐ⁻ⁿ⁾
When dividing exponents, if the bases are the same, you can simply subtract the exponents from the numerator and the denominator.
Smicha now has to make sure all the robots are built on time what’s this? I guess the future's not so different after all...
Exponents and Division – the Quotient of Powers Property exercise
-
Explain how to divide $2^5$ by $2^3$.
HintsRemember that $2^5=2\times 2\times 2\times 2\times 2$.
We can see that $2\times 2\times 2$ in the denominator of $\frac{2\times 2\times 2\times 2 \times 2}{2\times 2 \times 2}$ can cancel out three of the $2$'s in the numerator.
SolutionThe quotient of powers property says that dividing two powers with the same base is the same as subtracting the exponent of the denominator from the exponent of the numerator and raising the base to that power.
Generally, this can be stated as $\frac{a^m}{a^n}=a^{(m-n)}$.
$~$
Using the quotient of powers property with our example, we have:
$\frac{2^{\large 5}}{2^{\large 3}}=2^{(5-3)}=2^2$.
$~$
Looking at our example even more explicitly, we have that
${\large\frac{2^5}{2^3}}=\frac{2\times 2\times 2\times 2 \times 2}{2\times 2 \times 2}$.
Because we have the factor $2$ five times in the numerator and three times in the denominator we can cancel out three $2$'s in the denominator with three $2$'s in the numerator, giving us
$\frac{2\times 2\times 2\times 2 \times 2}{2\times 2 \times 2}=2^2$.
$~$
We can also come to the same conclusion by dividing $2^5=32$ by $2^3=8$:
$\frac{32}8=4=2^2$.
-
Determine the number of hard drives AA-RNO needs to store an entire copy of the internet.
HintsKeep the quotient of powers property in mind: subtract the exponents and raise the base to this power.
Here is an example:
Remember to subtract the exponent of the denominator from the exponent of the numerator... the order matters here!
Solutionthe quotient of powers property says that we should subtract the exponents and raise the common base to the result: $\frac{a^m}{a^n}=a^{(m-n)}$
$~$
So, if we have to divide the total brontobytes we need, $10^{25}$, by any decimal power with base 10, we only have to subtract the exponents and raise 10 to the resulting power.
$~$
For our hard drive options, we have:
$\frac{10^{\large 25}}{10^{\large 15}}=10^{(25-15)}=10^{10}$
and as well
${\large\frac{10^{25}}{10^{18}}}=10^{(25-18)}=10^{7}$
$~$
Pay attention to the order of subtraction: You have to subtract the exponent of the denominator from the exponent of the numerator, and not the other way around!
-
Decide which division the quotient of powers property can be used.
HintsThis power has basis $a$ and exponent $m$.
Keep in mind that the basis must match... not the exponents.
SolutionWe can apply the quotient of powers property to powers which have the same base. Then we only have to subtract the exponent of the denominator from the exponent of the numerator and raise the base to the result:
- ${\large\frac{10^{22}}{10^2}}=10^{(22-2)}=10^{20}$
- ${\large\frac{10^{22}}{10^{12}}}=10^{(22-12)}=10^{10}$
- ${\large\frac{10^{22}}{10^3}}=10^{(22-3)}=10^{19}$
- ${\large\frac{3^{17}}{3^5}}=3^{(17-5)}=3^{12}$
- ${\large\frac{3^{17}}{3^{10}}}=3^{(17-10)}=3^{7}$
- ${\large\frac{5^{19}}{5^{10}}}=5^{(19-10)}=5^{9}$
- ${\large\frac{5^{19}}{5^{3}}}=5^{(19-3)}=5^{16}$
- ${\large\frac{5^{19}}{5^{12}}}=5^{(19-12)}=5^{7}$
-
Examine the growth of the internet data volume between 3008 and 8008.
HintsIf you have powers with the same basis you can apply the quotient of powers property:
Subtract the exponent of the denominator from the exponent of the numerator, not the other way round.
Let's have a look at an example:
SolutionTo get the growth $g$ of the internet volume between 8008 and 3008, we have to solve the equation
$g\times 10^{12}=10^{25}$.
To get the factor $g$, we need to divide by $10^{12}$; so we have
$g={\large\frac{10^{25}}{10^{12}}}$.
Since we have two powers with the same basis, we can apply the quotient of powers property and subtract the exponents in the following way:
$g=10^{(25-12)}=10^{13}$.
Thus we can see that the internet data volume has grown by the factor of $10^{13}$.
Indeed, that is amazing growth!
-
Describe the quotient of powers property.
HintsRemember that $a^n=\underbrace{a\times ...\times a}_{\text{n times}}$
In this example, we can see that the two $3$'s in the denominator cancel out with two of the $3$'s in the numerator.
In this example, nothing in the denominator can cancel out with anything in the numerator.
SolutionThis is the formula for the quotient of powers property.
Let's talk about what it means. This property assists with simplifying powers, but only if they have the same basis.
When dividing powers with the same basis, you can simply subtract the exponent of the denominator from the exponent of the numerator and raise the common basis to the result.
-
Carry out the following divisions.
HintsKeep the common basis and subtract the exponents.
Pay attention to the order of subtraction. If you change the order of subtraction you'll get a negative exponent. This is also possible but wrong, for instance, for the following example:
The resulting exponent can also be zero.
$a^0=1$, as long as $a\neq 0$.
SolutionIf you have to divide two powers with the same basis, you only have to subtract the exponents in the right order: subtract the exponent of the denominator from the exponent of the numerator. The basis of the result stays the same.
- ${\large\frac{9^{12}}{9^{11}}}=9^{(12-11)}=9^1=9$
- ${\large\frac{3^{35}}{3^{33}}}=3^{(35-33)}=3^2=9$
- ${\large\frac{5^{5}}{5^{2}}}=5^{(5-2)}=5^3=125$
- ${\large\frac{4^{8}}{4^{8}}=4^{(8-8)}}=4^0=1$
- ${\large\frac{6^{13}}{6^{10}}}=6^{(13-10)}=6^3=216$
- ${\large\frac{7^{43}}{7^{21}}}=7^{(43-21)}=7^{22}$


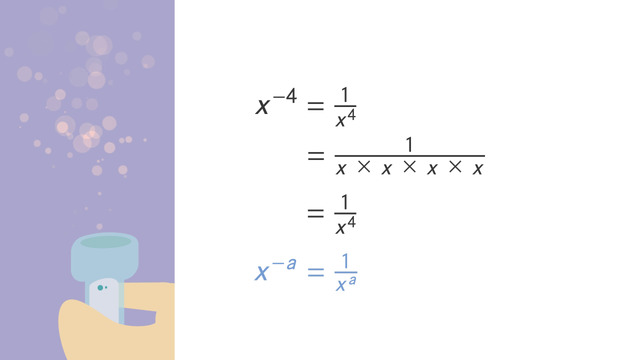













Very cool! And informative!