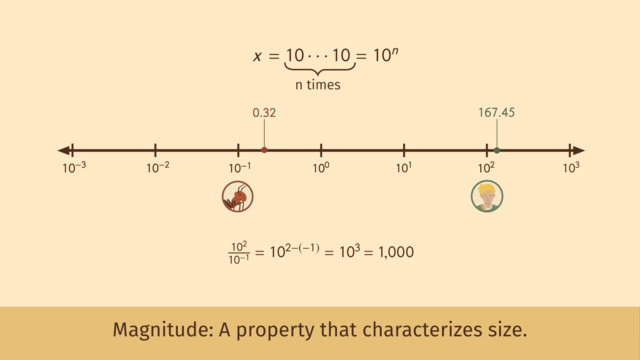
Estimating Quantities


Basics on the topic Estimating Quantities
After this lesson you will be able to compare and estimate quantities in the form of a single digit times a power of 10.
The lesson begins with rounding two values. It leads to converting the rounded numbers to their leading digit times a power of 10. It concludes with multiplying and dividing using the laws of exponents.
Learn how to estimate and compare quantities by helping Dr. Evil improve his dating chances on the Evil Match app!
This video includes key concepts, notation, and vocabulary such as: estimation or approximation (a value close enough to the right answer); precise estimate (derived by rounding so that only the leading digit remains); and leading digit (the first digit of the integer).
Before watching this video, you should already be familiar with the laws of exponents, simplifying expressions, and rounding numbers.
After watching this video, you will be prepared to use larger values and more ways of estimating and comparing the magnitudes of numbers, specifically scientific notation.
Common Core Standard(s) in focus: 8.EE.3 A video intended for math students in the 8th grade Recommended for students who are 13-14 years old
Transcript Estimating Quantities
Dr. Evil is a super-villian who loves spending time in his secret lair. But like everyone, Dr. E gets lonely sometimes. He signed up for the dating service Evil-Match but he still hasn't made any connections. Dr. E blames it on his bald head and hatches a devilish scheme. He will create a massive army of nano-bots that will destroy the hair of his competition. It's so crazy it just might work! To see if he can make his evil dream a reality, Dr. E will need to Estimate and Compare Quantities. Dr. E remembers the good old days, when he had a full head of hair. At his hair's peak, he had exactly one-hundred eighty-four thousand, three-hundred and sixty two hairs on his head. Now he only has seven thousand, eight-hundred and twenty. How many times more hair did he have back then compared to now? We can calculate that by dividing, but it would take a while to divide these numbers without a calculator. Since we don't need an exact answer, an estimate will be fine. Therefore, we can round each of the values to make the division simpler for us. Let's round 184,362 to the nearest hundred thousand. That's 200,000. But we can write this number in another form that makes division even simpler. The leading digit is 2. By factoring, we get that 200,000 is 2 times 100,000. Since there is a 1 followed by 5 zeroes, 100,000 is 10 to the fifth power. So our estimate for the hairs on young Dr. Evil's head is 2 times 10 to the 5th. Notice that it's equal to the leading digit times ten to the number of zeroes. Today, Dr. E only has 7,820 hairs on his head. Let's round that to the nearest thousand: 8,000. Because we see 3 zeros after the leading digit of the rounded number that's 8 times 10 to the 3rd. Let's calculate the ratio of Dr. E's hair back then to his hair now. That means we divide: 2 times 10 to the 5th, over 8 times 10 to the 3rd. Two over 8 reduces to 1 over 4. Using the laws of exponents, ten to the 5th over 10 to the 3rd is equal to ten to the quantity 5 minus 3. That's 10 to the second. Simplifying further gives us 100 over 4, which is equal to 25. Dr. E had about 25 times as much hair back then as he does now! Ah, those were the good old days! When he only need an estimate of the answer, we can round the numbers and write them as a digit times a power of ten, which makes our calculations simpler. Dr. E snaps out of his nostalgic daydream and gets back to work. Building a nano-bot army isn't going to be easy, so he first wants to estimate the scale of the challenge. About how many nano-bots will he need? First let's estimate the total number of hairs to be cut. Dr. Evil doesn't need an exact value, so he will round numbers in his calculation in order to simplify his work. First, Dr. Evil finds a value for the number of men on earth: three billion, seven-hundred-fifty-eight million, three-hundred thousand. Rounding to the nearest billion gives us 4 billion men. Because we count nine zeros after the leading digit of 4, we can write this as 4 times 10 to the 9th. That's a lot of people! So, how many hairs will Dr. E have to cut? There are 125,000 hairs on the average head. Rounding to the nearest hundred thousand gives us 100,000. Five zeros means 10 to the 5th. So altogether, about how many hairs will Dr. E's nanobots need to cut? Let's multiply the number of men, times the number of hairs per person. That's 4 times 10 to the 9th times 10 to the 5th. Using another law of exponents, 10 to the 9th times 10 to the 5th is equal to 10 to the quantity 9 plus 5, which equals 10 to the 14th. So Dr. E's army of nanobots will have to cut about 4 times 10 to the 14th individual hairs. That's a lot of hairs! What other information does Dr. Evil need to figure out the total number of nano-bots he'll have to produce? He needs to know how many hairs each nano-bot can cut before it expires, which is eight million, two hundred and fifty thousand. Let's round that to 8 million which can also be written 8 times 10 to the 6th hairs per bot. We divide the total number of hairs to cut by the hairs per bot in order to get the number of bots we'll need to complete the job. Four times 10 to the 14th divided by 8 times 10 to the 6th. Four over 8 reduces to 1 over 2. Ten to the 14th divided by 10 to the 6th is 10 to the 8th. That's one-half times 10 to the 8th. How do we simplify this? One half is 0.5. or 5 over 10. Cancelling this 10 with one 10 here gives us 10 to the 7th. He would need over 50 million nano-bots for his plan to suceed? That would be way too much work, even for Dr. Evil. But what can he do to improve his chances on the Evil-Match app? While Dr. Evil brainstorms other possibilities, let's review what we learned. When working with large numbers estimating can be an efficient and revealing method for completing calculations. When we encounter a large number we can estimate that number by rounding. We can then convert the number to the leading digit times a power of 10. By using the laws of exponents, numbers in this form can be multiplied and divided efficiently. Looks like Dr. E is back on the Evil-Match app. Or is he?