Determining a Unique Triangle Given Two Sides and a Non-included Angle.
Basics on the topic Determining a Unique Triangle Given Two Sides and a Non-included Angle.
After this lesson you will understand the conditions required for determining a unique triangle, given two sides and a non-included angle.
The lesson begins with a review of unique triangles and the different measurements that make up all triangles. It continues by showing three examples of constructing triangles given the measurements of two sides and a non-included angle (obtuse, acute, and right).
Learn about unique triangles by helping the Pharaoh (and his cat) build a waterslide!
This video includes key concepts, notation, and vocabulary such as: unique triangle (a triangle that can only be drawn one way); acute angle (an angle that is less than 90 degrees); right angle (an angle that measures 90 degrees); and obtuse angle (an angle that is greater than 90 degrees).
Before watching this video, you should already be familiar with the concept of unique triangles, and different kinds of angles.
After watching this video, you will be prepared to explore two-dimensional figures that result from slicing three-dimensional figures.
Common Core Standard(s) in focus: 7.G.A.2 A video intended for math students in the 7th grades Recommended for students who are 12-13 years old
Transcript Determining a Unique Triangle Given Two Sides and a Non-included Angle.
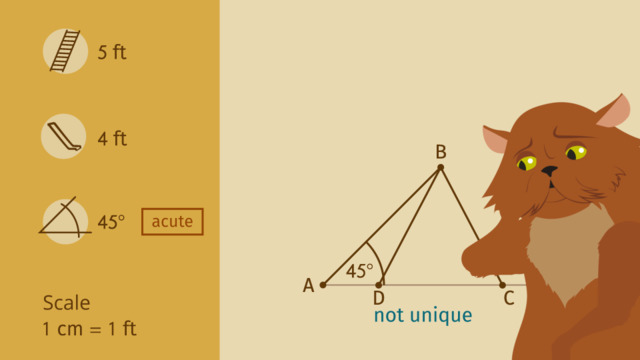
Pharaoh Ahmose has built a fabulous pool to cool himself from the Egyptian heat. But Khufu, the pharaoh's cat, needs a fun diversion. So, Pharoah Ahmose commands his architect to build a waterslide that meets Cat Khufu's high standards. In order to create a truly special waterslide, the architect will need to understand the conditions required for determining a unique triangle given two sides and a non-included angle. The waterslide creates a triangle with the ladder, slide, and ground. There are so many ways to construct the triangular slide. What measurements make up a triangle? Well, a triangle has three sides and three angles. That's a total of six measurements. But we've learned before that sometimes given just three measurements allows us to find a unique triangle. Recall that a unique triangle is a triangle that can only be drawn one way. Pharoah Ahmose's architect already has a ladder that is 5 feet long, and a slide that is 4 feet long. Therefore, Pharoah Ahmose commands that the ladder make a 45 degree angle, that's an acute angle, with the ground. Let's see by constructing a sketch of the triangular slide, using a ruler protractor and compass. To fit our drawing on paper, we'll scale our diagram so that 1 centimeter on paper represents 1 foot. First, let's start at point A and use a ruler to draw a ray representing the ground. Now we place our protractor on point A, and measure a 45 degree angle from the horizontal. We draw another ray to complete the angle and label it with 45 degrees. Next, let's measure 5 centimeters along this ray to represent the 5 foot ladder. Let's label the ladder part as segment 'AB'. We'll use our compass to capture the length of 4 centimeters from our ruler. Placing the needle of the compass on point 'B', we draw a circle with a radius of 4 centimeters. This shows us where we could possibly place the 4 foot slide. We can see that there are two places where the 4 foot slide can intersect with the ground to complete our triangle. There are two different triangles. Triangle ABC and triangle ABD These two triangles are clearly different. Notice the dimensions we were given are two side lengths and an angle and the angle is not in between them. The command from Pharaoh Ahmose did not specify a unique triangle. It is true that given measurements of two sides and a non-included, acute angle, do not specify a unique triangle. This result is quite unsatisfactory! Cat Khufu rejects this plan! Perhaps an obtuse angle will be more to Khufu's liking! Pharoah Ahmose commands that the slide must have the same 5 foot ladder that intersects with the ground now at an obtuse angle of 120 degrees. Additionaly, he wants to use the 10 foot slide to complete the project. Let's construct a sketch of the pharoah's new idea to see if the result is a unique triangle. Again, using a ruler as a straight edge draw a ray starting at point 'A' to represent the ground. From point 'A' we use our protractor to measure 120 degrees and construct another ray. With our ruler, we measure 5 centimeters along the ray and mark point B. Line segment 'AB' represents our 5 foot ladder. We'll use our compass to now capture the length of 10 centimeters from our ruler. Placing the needle of the compass on point 'B', we draw a circle with the radius of 10 cm to represent the new 10 foot slide. How many triangles can be constructed using these two sides and a non-included obtuse angle? Just one! The conditions of the pharaoh resulted in a unique triangle! We can see that given measurements for two sides and a non-included, obtuse angle, specify a unique triangle. But Cat Khufu is a clever cat, and he knows this slide just won't do. So, Pharoah Ahmose commands that the ladder stay 5 feet long and the slide 10 feet long but the non-included angle be 90 degrees, a right angle. This means we can just adjust the obtuse angle from our earlier sketch to be 90 degrees. How many triangles can be constructed using these two sides and a non-included right angle? Again, just one! Notice that given measurements for two sides and a non-included right angle also result in a unique triangle. Does this slide meet Cat Khufu's expectations? Yes! While the slide is being constructed, let's review the conditions for determining a unique triangle given two sides and a non-inluded angle. We know our measuremtnets give us a unique triangle when the triangle can only be drawn one way. Two sides and a non-included acute angle do not determine a unique triangle. But two sides and a non-included obtuse angle do determine a unique triangle. And two sides and a non-included right angle also determine a unique triangle. Cat Khufu is eager to test this unique slide! Right triangle, wrong cat.