Connections Between Adding and Subtracting, Multiplying and Dividing


Basics on the topic Connections Between Adding and Subtracting, Multiplying and Dividing
The inverse of addition is subtraction and vice versa. In other words, if a number, like 5, is added to another number, like 7 (to get 7+5=12), then the way to get back to the original number, 7, is to subtract 5 from 12. Similarly, if a number, like 5, is subtracted from another number, like 7 (to get 7-5=2), then the way to get back to the original number, 7, is to add 5 to 2. Similarly, multiplication and division are also inverses of each other. Learn more about the inverse relationships between addition and subtraction, and multiplication and division, by helping Jerome the Gnome figure out how he can vacation in Boca Raton without turning into stone. Common Core Reference: CCSS.MATH.CONTENT.5.NBT.B.6, CCSS.MATH.CONTENT.5.NBT.B.7
Transcript Connections Between Adding and Subtracting, Multiplying and Dividing
Jerome the Gnome sits in his home, with dreams of vacationing in Boca Raton. To confirm this fact, you should ask someone. Do gnomes turn to stone when kissed by the sun? In order for Jerome to elude this plight, he must do well to avoid the sunlight. Jerome'll visit a witch he can trust, he receives ingredients for a special pixie dust. He must collect all the items on the list to help him avoid this metamorphosis.
Connections Between Adding and Subtracting, Multiplying and Dividing
What a wonderful idea, it's got some traction! Use opposite operations like addition and subtraction! Also, though it may be difficult to envision, another pair of opposites are multiplication and division. Jerome needs to collect sunflower seeds, ladybugs and forget-me-not petals.
Sunflower seeds - The additive inverse property
While riding Dale the Snail through the forest, Jerome notices a hole in his napsack! After fixing the hole in his napsack Jerome needs to collect the same number of sunflower seeds he lost. Jerome had 200 sunflower seeds in his napsack, but lost 40 on the way leaving Jerome with 160 sunflower seeds. Jerome comes back with 40 sunflower seeds to replace the ones he lost. So 200 seeds minus the 40 seeds Jerome lost, PLUS the 40 seeds he collected gives him back the 200 seeds he needed. Whenever you add a number to its opposite, the result is always zero. This the Inverse Property of Addition.
Ladybugs - Multiplication
The next item on the list is 12 ladybugs. Jerome can only catch 4 ladybugs at a time. So how many times does Jerome have to hunt ladybugs in order to reach his goal of 12? Adding 4 three times gives you 12. Another way to write this is to use the definition of multiplication, giving us 4 times 3. When adding a number to itself multiple times, it may be easier to write it as a multiplication problem. Here, we see that 'a' is added n' times, giving us 'n' times 'a'.
Forget-me-not petals - The multiplication inverse property
The last items on the list are the forget-me-not petals. Each flower Jerome shakes yields 5 forget-me-not petals. Like before, this can be written with addition like this. Or since all the addends are the same, we can write this as a multiplication problem as well. Just like addition and subtraction are opposite operations, multiplication and division are also opposite operations. Since Jerome has 15 petals that he needs to divide into three jars Jerome puts an equal number of petals into each of the three jars. This process of splitting a number into equal parts is called division. Each flower yielded Jerome 5 forget-me-not petals and Jerome shook three flowers which he then needs to divide into three jars. This is the Inverse Property of Multiplication. If you multiply and then divide by the same number you get back your original number.
With the list now done, Jerome dreams of the sun. The witch keeps her promise and sprinkles the glitter, then Jerome celebrates with a twinkle and a flitter. Jerome planned to lie down just for a brief respite, no shade was welcome only sunlight. But all the day under the sun, Jerome willl learn quickly, sunburns just aren't fun.
Connections Between Adding and Subtracting, Multiplying and Dividing exercise
-
Explain how the Inverse Properties of Addition and Multiplication work.
HintsTo split $10$ pieces of cake between $5$ people, you have to divide $10$ by $5$:
$10\div 5=2$.
So each person gets $2$ pieces of cake.
Instead of adding a number, you can also use multiplication:
$4+4+4+4+4+4=6\times 4=4\times 6$.
If you have $5$ pieces of cake and you give away exactly this number of pieces, then you have no pieces of cake left over at all: $5-5=0$ or $5+-5=0$.
SolutionThis $\mathbf{+}$ is the sign for addition.
Let's have a look at the following example Sunflower seeds:
Jerome had $200$ seeds in his knapsack, but he lost $40$ seeds. So he has to collect $40$ seeds to get back to $200$ seeds.
This lead to
- $200-40=160$
- $200-40+40=200$
$a+-a=0$ or $-a+a=0$.
This $\mathbf{\times}$ is the sign for multiplication.
Once again let's have a look at Jerome and what he needs for his potion. He still needs forget-me-not petals.
Each flower Jerome shakes has $5$ petals. Together he gets
$5+5+5=5\times 3=15$ petals.
He splits the whole number on $3$ jars. So he has to put
$15\div3=5$
petals in each jar.
To figure this out, we used the inverse property of multiplication:
$a\times b=ab$ and $\frac{ab}b=a$.
-
Summarize your knowledge about the Definition of Multiplication.
HintsCompare the expressions:
- $3+3+3+3+3=?$
- $3\times 5=?$
- $3+5=?$
- $3^5=?$
One beagle plus one beagle, plus one beagle plus one beagle, is the same as four beagles.
$1+1+1+1=1\times 4=4$
SolutionJerome needs $12$ ladybugs.
He can catch $4$ ladybugs at a time. How many times does Jerome have to catch ladybugs to get $12$ ladybugs in total:
- $4+4=8$
- $4+4+4=12$
$4+4+4=4\times 3$.
In general, you can write the sum of $n$ times the summand $a$ as follows:
$a+a+\cdots+a=n\times a$.
-
Place the equations with the correct properties and definition.
HintsThe inverse property of addition is given by $a+-a=0$ or $-a+a=0$.
The inverse property of multiplication is given by $a\times b=ab$ and $\frac{ab}b=a$.
Multiplication is a shorter way to write a sum of repeating summands
$a+a+\cdots+a=n\times a$.
For example, $2+2+2+2+2+2=6\times 2=2\times 6=12$.
SolutionLet's start with the inverse property of addition:
$a+-a=0$ or $-a+a=0$.
- $4+-4=0$
- $27+3-3=27$
- $-b+b=0$
- $2\times 7=7+7$
- $k+k+k+k=4\times k$
- $3+3+3+3=4\times 3$
$a\times b=ab$ and $\frac{ab}b=a$.
- $5\times 3\div 3=5$
- $m\times 2\div 2=m$
- $(bc)\div c=b$
-
Complete the equations to make true statements. (+ multiplication)
HintsHere is an example for the inverse property of addition:
$27+5-5=27$.
Here is an example for the inverse property of multiplication:
$3\div 4\times 4=3$.
Instead of adding $5+5+5+5+5$ you can also write a product:
$5\times 5=25$.
SolutionHere we use...
- ...the inverse property of addition: $a+-a=0$ or $-a+a=0$.
- ...the inverse property of multiplication: $a\times b=ab$ and $\frac{ab}b=b$ or $a\times b\div b=a$.
- ...the definition of multiplication: $a+a+a+a+a=5\times a$ - just count the number of summands.
- $5\times 3\div 3 = 5$ - this is the inverse property of multiplication.
- Once again the inverse property of multiplication: $p\div p\times r=r$.
- The next three points are examples for the inverse property of addition $5+-5=0$.
- $-7+7=0$.
- $33+5-5=33$.
- The definition of multiplication: $6+6+6+6=4\times 6=24$.
-
Determine how many ladybugs Jerome found.
HintsJerome collects $4$ ladybugs each time:
- $4$ ladybugs one time
- $4+4$ ladybugs two times
- ...
You can also multiply $4$ by $3$.
Just add $4$ three times.
SolutionJerome collects $4$ ladybugs at one time:
So he collects
- $4+4=8$ ladybugs two times
- $4+4+4=12$ ladybugs three times
$4+4+4=4\times 3=12$.
Keep in mind that multiplication is a shorter way to write a sum with repeating summand $a$:
$a+a+\cdots+a=n\times a$.
-
Figure out which equations represent how many of each item Jerome has lost.
HintsThe inverse property of addition: $5+6-6=5$.
The definition of multiplication:
$6+6+6+6+6=5\times 6=6\times 5=30$.
The inverse property of multiplication: $7\times 3\div 3=7$.
Solution- Blueberries: Loosing $5$ blueberries can be written as $-5$. So, using the inverse property of addition, we conclude that $20-5+5=20$.
- Twigs: Once again we use the inverse property of addition: $25+-13+13=25$.
- Coffee beans: $3$ times $5$ can be written as $5+5+5=3\times 5=15$, using the definition of multiplication.
- Fish scales: Lastly, we use the inverse property of multiplication to examine the number of fish scales: $6\times 4\div 4=6$.



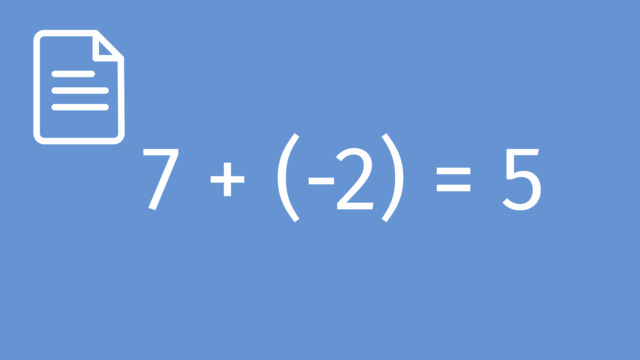










Hi @Hunter B.,
we are so happy that you enjoy our videos!
Let us know if you have any questions. We're always glad to help.
cool video, I learned a lot