Angles Created When Parallel Lines are Cut by a Transversal
- Angles Created When Parallel Lines are Cut by a Transversal – Introduction
- Angles Created When Parallel Lines are Cut by a Transversal – Definition
- Angles Created When Parallel Lines are Cut by a Transversal – Guided Practice
- Angles Created When Parallel Lines are Cut by a Transversal – Summary
- Angles Created When Parallel Lines are Cut by a Transversal – Frequently Asked Questions

Basics on the topic Angles Created When Parallel Lines are Cut by a Transversal
Angles Created When Parallel Lines are Cut by a Transversal – Introduction
Parallel lines cut by transversals form various angles with distinctive properties. In geometry, understanding these angle relationships is crucial as they establish the foundation for more complex concepts and real-world applications. This topic will explore how different angles relate to one another when parallel lines are cut by a transversal.
Angles Created When Parallel Lines are Cut by a Transversal – Definition
When two parallel lines are intersected by a transversal, eight angles are formed. Each set of angles has unique characteristics that can help to determine unknown angle measures.
Parallel lines are straight lines in a plane that do not intersect, no matter how extended. A transversal is a line that crosses at least two other lines. The angles formed when a transversal cuts through parallel lines can be categorized into several types, including corresponding, alternate interior, alternate exterior, same-side interior, and same-side exterior angles.
| Angle Relationship | Description | Example |
|---|---|---|
| Vertical Angles | Vertical angles are pairs of opposite angles made by two intersecting lines. They are always equal to each other. | (b, d), (a, c), (f, h), (e, g) |
| Corresponding Angles | Corresponding angles are pairs of angles that are in similar positions at each intersection where a straight line crosses two parallel lines. | (b, f), (c, g), (a, e), (d, h) |
| Alternate Interior Angles | Alternate interior angles are pairs of angles on opposite sides of the transversal but inside the two lines. These angles are equal when the lines are parallel. | (c, e), (d, f) |
| Alternate Exterior Angles | Alternate exterior angles are pairs of angles on opposite sides of the transversal but outside the two lines. These angles are equal when the lines are parallel. | (b, h), (a, g) |
| Supplementary Angles | Supplementary angles are pairs of angles whose sum is 180 degrees. They often appear adjacent to each other but can also be separated spatially. | (b, c), (c, d), (d, a), (a, b), (e, f), (f, g), (g, h), (h, e) |
Angles Created When Parallel Lines are Cut by a Transversal – Guided Practice
Let's guide through another example:
You're given two parallel lines, Line C and Line D, intersected by a transversal, Line E. If Angle 1 measures 50 degrees, can you find the measures of Angles 3, 5, and 7?
Angles Created When Parallel Lines are Cut by a Transversal – Summary
Key Learnings from this Text:
- The angles formed when a transversal cuts through parallel lines are categorized into corresponding, alternate interior, alternate exterior, same-side interior, and same-side exterior angles.
- Corresponding angles and alternate angles (both interior and exterior) are equal in measure.
- Same-side interior and same-side exterior angles are supplementary.
- Understanding these angle relationships is essential for solving geometric problems.
This knowledge is not only pivotal for classroom success but also for fields such as architecture and engineering. We encourage you to continue exploring with interactive practice problems and other resources on our platform.
Angles Created When Parallel Lines are Cut by a Transversal – Frequently Asked Questions
Transcript Angles Created When Parallel Lines are Cut by a Transversal
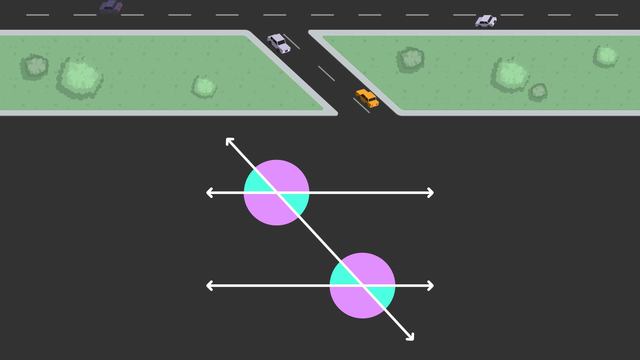
Angles created when parallel lines are cut by a transversal. These lines here are parallel and will never cross. A line that cuts through parallel lines is called a transversal. This grouping of lines has created eight angles which we can label with variables until we know the measurements. Each angle is related to another, some are congruent and some are supplementary. Remember, congruent means that the angles have the same measurement, so they are equal. Supplementary angles are two angles that have a sum of one hundred eighty degrees. These pairs can be any two angles directly next to one another since they are on a straight line which is one hundred eighty degrees. Angles g and h are supplementary, as well as e and f, and many other pairs. But, supplementary angles don't need to be next to each other. Any pair of angles that has a sum of one hundred eighty degrees is considered supplementary. For example, angles a and f are considered supplementary, because the angles have a sum of one hundred eighty. Vertical angles are a pair of angles opposite from one another, and they are congruent. Here, we have four pairs of vertical angles, a and c, b and d, e and g, and also f and h. Alternate exterior angles are a pair of angles on the outside of the parallel lines but are on opposite sides. These angle pairs are also congruent. A and g are an alternate exterior angle pair, as well as b and h. Alternate interior angles are a pair of angles on the inside of the parallel lines but on opposite sides of the transversal. The angle pairs of c and e, and d and f are congruent because they are alternate interior angles. Corresponding angles refer to angles that are in the same position but on a different parallel line of the two. These angles are congruent, and some of the pairs include b and f, or d and h, amongst other pairs. Let's practice applying what we learned by looking at this map that contains two parallel roads cut by a transversal road. What angle is d paired with to create vertical angles? Angle b is vertical with angle d and they are congruent. Name the angle that is an alternate exterior angle pair with angle x. Angle c and x are alternate exterior angles and therefore are congruent. What angle is corresponding with angle y? Angle b is because it is in the same position, therefore it is congruent. If angle w had a measurement of seventy degrees, what would be the measurement of angle y? Since this pair is vertical, they would both be seventy degrees. Once we know just one of these angles, we can actually find all of the remaining angles. If angle y is seventy degrees, then so is b since they are corresponding, and therefore d is as well since it is y's alternate exterior angle. The remaining angles must be supplementary with seventy degrees, and in order to find that we can subtract seventy from one hundred eighty to get one hundred ten. Let's summarize what we have learned. Two parallel lines cut by a transversal create eight angles, all of which are related to each other. Angles that are congruent have the same measurement, and angles that are supplementary add to one hundred eighty degrees. Understanding angle measurements and relationships is important when it comes to maps, architecture, and engineering.
Angles Created When Parallel Lines are Cut by a Transversal exercise
-
Vertically opposite angles.
HintsVertically opposite angles are congruent (the same size). They form an X shape.
These angles are vertically opposite.
- $x = x$
- $y = y$
Solution$c$ is vertically opposite to $a$, $a = c$.
The opposite angles in a cross (X shape) are the same size or congruent.
-
Find the supplemetary angles.
HintsSupplementary angles form a straight line as their sum is $180^\circ$. Therefore, we are looking for angles which would add to $a$ and make a straight line.
We can see on the image $x$ and $y$ are supplementary.
$x + y = 180$.
There are $3$ correct answers here.
SolutionThe supplementary angles to $a$ are $b$, $d$ and $f$.
- $a + b = 180$
- $a + d = 180$
- $a + f = 180$
-
What are the values of the angles?
HintsAngles in a straight line are supplementary and have a sum of $180^\circ$. We can find a missing angle by doing the calculation $180 - 50 = 130$
Interior alternate angles are congruent and can be found forming a Z shape on the opposite sides of the transversal line.
Solution- $110^\circ$ is corresponding with the angle of $110^\circ$ at the bottom.
- $70^\circ$ is in a straight line with $110^\circ$.
- $95^\circ$ is interior alternate with the angle of $95^\circ$.
- $85^\circ$ is a straight line with $95^\circ$.
-
What is the angle?
HintsAngles are congruent if they are the same. All the angles marked in green are congruent to $106^\circ$.
Angles are supplementary if their sum is $180^\circ$. All the angles marked in green are supplementary with $106^\circ$.
Solution$106^\circ$ (Exterior alternate angles)
- The angle is congruent to $106^\circ$
- Both angles are on the exterior of the parallel lines
- Both angles are on the opposite side of the transverse line.
-
Congruent angles
HintsAlternate angles are on the opposite side of the transverse line. The interior ones form a Z shape.
Corresponding angles are in the same position and can form an F shape with each other.
Exterior alternate angles are on the opposite side of the transverse line and the exterior of the parallel lines.
Vertically opposite angles are on the opposite side forming an X shape.
Solution- Interior alternate angles form a Z shape on the opposite side of the transverse line.
- Exterior alternate angles are on the exterior opposite sides of the transverse line.
- Corresponding angles angles form a F shape in the same positions.
- Vertically opposite angles form a X shape and are opposite each other.
-
Find the missing angle.
HintsTo help with this question we need to use the fact that the sum of angles in a triangle is $180^\circ$. For example, in the image here, we need to find the values of $b$ and $c$ in order to find $a$.
To find the angles at $b$ and $c$ we are using the angle facts we know. For example congruent angles, that have the same value as a given angle and supplementary angles which sum to $180^\circ$.
Solution$a = 32^\circ$
- $65^\circ$ is in a straight line with $115^\circ$, this is supplementary $(180^\circ - 115^\circ = 65^\circ)$
- $83^\circ$ is vertically opposite to $83^\circ$, this is congruent
- $a = 32^\circ$, a triangle with $65^\circ$ and $83^\circ$ (Angles in a triangle sum to $180^\circ$)
- $180^\circ - 65^\circ - 83^\circ = 32^\circ$