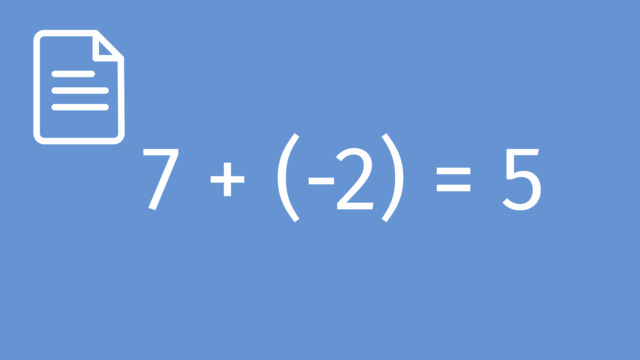Subtracting Rational Numbers by Adding the Inverse
- Subtracting Rational Numbers by Adding the Inverse
- Subtracting by Adding the Inverse – Explanation
- Subtracting Rational Numbers by Adding the Inverse – Example
- Subtracting Rational Numbers by Adding the Inverse – Guided Practice
- Subtracting Rational Numbers by Adding the Inverse – Summary
- Subtracting Rational Numbers by Adding the Inverse – Frequently Asked Questions
Learning text on the topic Subtracting Rational Numbers by Adding the Inverse
Subtracting Rational Numbers by Adding the Inverse
In this text, we're tackling a handy mathematical technique Subtracting Rational Numbers by Adding the Inverse. This method can simplify your calculations and save you time. Don't let the terminology intimidate you — we're going to explore this topic step by step, ensuring you grasp the concept and learn how to apply it effectively.
Subtracting by Adding the Inverse – Explanation
When we talk about subtracting rational numbers by adding the inverse, we're essentially discussing a more efficient way to perform subtraction.
A rational number is any number that can be expressed as the quotient or fraction $\frac{p}{q}$ of two integers, where $q \neq 0$. This includes integers, fractions, mixed numbers, and finite and repeating decimals.
The inverse of a number refers to its additive inverse, which is the number that, when added to the original number, results in zero. For example, the additive inverse of $7$ is $-7$ because $7 + (-7) = 0$.
Subtracting a negative rational number is particularly interesting because you effectively add the opposite of a negative, which is a positive. For instance, subtracting $-3$ is the same as adding $3$. This makes calculations easier because adding is often more straightforward than subtracting, especially when dealing with negatives.
Subtracting Rational Numbers by Adding the Inverse – Example
Let's go through an example to see this process in action.
Subtract $\frac{2}{3}$ from $3$ using the inverse.
- Identify the number to subtract: We want to subtract $\frac{2}{3}$ from $3$.
- Find the inverse: The inverse of $\frac{2}{3}$ is $-\frac{2}{3}$.
- Add the inverse: Perform the addition $3 + (-\frac{2}{3})$.
Illustration request: A number line with $3$ on it and then showing a move of $-\frac{2}{3}$ to the left, landing at $2\frac{1}{3}$.
- Result: $3 + (-\frac{2}{3}) = 2\frac{1}{3}$.
Let’s now take a look at subtracting a negative rational number.
Subtract $-\frac{4}{5}$ from $2$ using the inverse.
- Identify the number to subtract: We want to subtract $-\frac{4}{5}$ from $2$.
- Find the inverse: The inverse of $-\frac{4}{5}$ is $\frac{4}{5}$ because the additive inverse of a negative number is its positive counterpart.
- Add the inverse: Perform the addition $2 + \frac{4}{5}$.
Illustration request: A number line with $2$ on it and then showing a move of $\frac{4}{5}$ to the right, landing at $2\frac{4}{5}$.
- Result: $2 + \frac{4}{5} = 2\frac{4}{5}$.
Subtracting Rational Numbers by Adding the Inverse – Guided Practice
Now, let's do a guided practice together.
Now apply this to your independent practice!
Subtracting Rational Numbers by Adding the Inverse – Summary
Key Learnings from this Text:
- To subtract a rational number, add its additive inverse to the other number.
- The additive inverse of a number is what, when added to the original number, equals zero.
- This method can simplify the process, especially with fractions and negative numbers.
Keep practicing this technique, and you'll soon master subtracting rational numbers with ease. Don't forget to check out other interactive practice problems and learning materials on our platform!
Subtracting Rational Numbers by Adding the Inverse – Frequently Asked Questions
Subtracting Rational Numbers by Adding the Inverse exercise
-
Define the keywords.
Hints$3$ and $-3$ are additive inverses because $3 + -3 = 0$
Rational numbers include integers, fractions and decimals.
Examples of rational numbers include -
Integers: $5, 7, -4, 126$
Fractions: $\frac{3}{5}, \frac{9}{2}, 5\frac{7}{8}$
Decimals: $4.2, 7.0451, 0.\dot{1}\dot{7}$
Solution- An additive inverse is a pair of numbers that, when added together, equal zero.
- An integer is a whole number.
- A rational number is any number that can be expressed as the quotient or fraction $\frac{p}{q}$ of two integers, where $q \neq 0$.
- A fraction is a part of a whole.
-
Find the maths sentence that uses the additive inverse.
HintsAdditive inverses cancel each other out. The additive inverse of $11$ is $-11$.
Subtracting a number is the same as adding its inverse. For example $6 - 2 = 6 + -2$.
Example: $8 - -3$
- Identify the number to subtract: We want to subtract $-3$ from $8$.
- Find the inverse: The inverse of $-3$ is $+3$.
- Add the inverse: The equivalent math sentence is $8 + 3$.
The equals sign does not always mean find the answer, here $=$ means the two statements are equivalent to each other.
Solution$3 - 2 = 3 + -2$
$5 - -4 = 5 + 4$
$5 - 4 =5 + -4$
$6.1 - -2 =6.1 + 2$
-
Choose the correct answer for each calculation.
HintsFirst,
- Identify the number to subtract.
Then,
- Find the inverse.
Finally,
- Add the inverse
Solution$4 -2\frac{1}{2} = 4 + -2\frac{1}{2} =$ $\bf{1\frac{1}{2}}$
$9 - -3 = 9 + 3 =$ $\bf{12}$
$8 - -1.6 = 8 + 1.6 =$ $\bf{9.6}$
-
Solve the subtractions.
HintsTo subtract a rational number, add its additive inverse to the other number.
The additive inverse of a number is what, when added to the original number, equals zero.
An example:
$8 - -2\frac{2}{5} = 8 + 2\frac{2}{5} = 10\frac{2}{5}$
Solution$3 - 1.5 = 3 + -1.5 = \bf{1.5}$
$7 - -3\frac{1}{4} = 7 + 3\frac{1}{4} = \bf{10\frac{1}{4}}$
$9 - 5\frac{1}{4} = 9 + -5\frac{1}{4} = \bf{3\frac{3}{4}}$
$4 - - 0.5 = 4 + 0.5 = \bf{4.5}$
-
What is $5 - -2$?
HintsFind the additive inverse of $-2$.
Now add the additive inverse to $5$ to find the answer.
A similar example:
$8 - - 6 = 8 + 6 = 14$
Solution$5 - -2 = 5 + 2 = 7$
-
Solve the calculations and place in order from smallest to largest.
HintsSolve each subtraction first using additive inverses.
Write the solutions down and order them from the smallest answer to the largest answer.
SolutionThe correct order is:
$\bf{6- 4.9, 10 - 5\frac{1}{2}, 5 - -1.2, 8 - -1\frac{3}{5}}$
because
$6- 4.9 = 6 + -4.9 = 1.1$
$10 - 5\frac{1}{2} = 10 + -5\frac{1}{2} = 4\frac{1}{2}$
$5 - -1.2 = 5 + 1.2 = 6.2$
$8 - -1\frac{3}{5} = 8 + 1\frac{3}{5} = 9\frac{3}{5}$