Computing the Slope of a Line

Basics on the topic Computing the Slope of a Line
A non-vertical line has a steepness, known as its slope. Given any two points on a line, the slope is equal to the difference, or change, of their y-coordinates divided by the difference, or change, of their x-coordinates. The change in y over the change in x is always the same, no matter which two points are given, and thus characterizes a line. Find out how Grandpa Lindbergh uses this computation to determine how steep of a flight path can his airplane take after an upgrade. Common Core Reference: CCSS.MATH.CONTENT.8.FA.3
Transcript Computing the Slope of a Line
Grandpa Lindbergh is one of the most famous aviators ever. He's always on the look-out for things to buy for his favorite plane...
In the plane's cockpit, Grandpa just installed some of the latest and greatest technology that money can buy. Today, he's gonna finally test it out and see how steep he can fly the plane. To do this, Grandpa Lindbergh will need help computing the slope of a line. Up, up, and away!
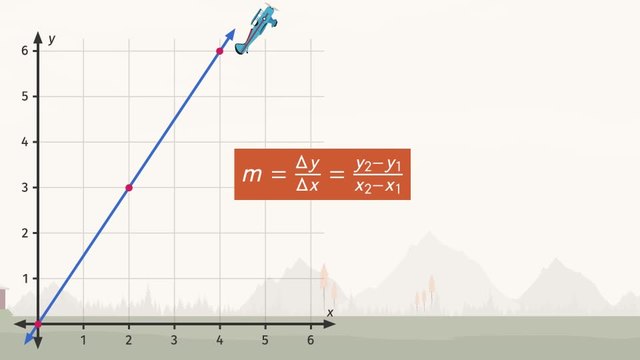
Looking at Grandpa’s flight path we can identify the coordinates of at least three points on the graph. Let’s take a look: To calculate the steepness of the flight path, we need to figure out the slope of the line. We can do this by using any two points on the line and plugging them into the slope formula. The slope formula is 'm' is equal to delta 'y' over delta 'x'. Delta is mathematical shorthand for change, or difference. That means it's the change in 'y' divided by the change in 'x'. The result, 'm', measures the steepness of the line connecting the two points.
Let’s plug in the coordinates for point 'a' and point 'b' into the slope formula. It doesn't matter which ordered pair you put first and which you put second just be consistent in how you order the 'x' and 'y' coordinates. Ok, we're going to use point 'a' as the first ordered pair and point 'b' as the second ordered pair. We plug in 3 for 'y' 2, 0 for 'y1', 2 for 'x2', and 0 for 'x1' which gives us the quantity '3 minus 0' divided by the quantity '2 minus 0' which is 3 over 2. This means for every increase of 2 unit on the x-axis there is an increase of 3 units on the y-axis.
A quick way to determine the slope is to draw a slope triangle on the line. Using line segment AB as the hypotenuse draw in a right triangle below the line. Remember, the hypotenuse is the longest side of a right triangle. It's also the side that's opposite the right angle. Just as we saw before, the change in 'y' is equal to 3 and the change in 'x' is 2. This is the same as what we calculated with the slope formula since it equals 3 over 2.
Let’s try two different points on the same line. This time, we’ll plug the coordinates for point 'a' and point 'c' into the formula. Once again, 'x1' is 0 and 'y1' is 0 but this time, 'x2' is 4 and 'y2' is 6. Subbing these values in gives us the quantity '6 minus 0' divided by the quantity '4 minus 0'. Simplifying like before, 'm' is equal to 3 over 2. How about that! The slope is the same as before. Don’t forget to draw in the slope triangle. Here, we can see that the change in 'y' is 6, and the change in 'x' is 4 and, 6 divided by 4 gives us, once again 3 over 2.
Let’s try it a third time but this time, we won’t use the ordered pair of point 'a' - just to check if that makes a difference. For point 'b' and point 'c', we again use the slope formula. Since we've already done it twice, let's go a bit more quickly. Once again, 'm' is equal to 3 over 2. And from the slope triangle we can see the slope is the same for these points too!
Let's summarize what we've learned. We know that the slope of a line can be calculated by plugging any two points of the line into the slope formula. We also know that the slope of a line is the same for ANY two points along that line. We can choose 'a' and 'b', 'b' and 'c', or 'a' and 'c'. We can extend what we've learned to write a rule about slope triangles. We learned that slope triangles created on one line, no matter what two points are used, will be similar triangles. Similar triangles share the same ratio between their sides, and always have the same angle measures.
Grandpa is really excited because everything seems to be working... Whoops! Wrong button...maybe he got a little too excited.
Computing the Slope of a Line exercise
-
Describe how to find the slope of the line given two points.
HintsKeep rise over run in mind to remember the order of division in the slope formula.
Pay attention to the order of subtraction.
SolutionThe slope of any non vertical line can be found using the slope formula.
Remember: rise over run.
The slope formula is given by dividing the change in $y$ by the change in $x$:
$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$.
We can now apply this formula to the two given points $A(0,0)$ and $B(2,8)$:
$m=\frac{8-0}{2-0}=\frac82=4$.
-
Find the slope of the line given a graph.
HintsThe slope tree helps you to remember the slope of different lines.
Use the slope formula: $m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
An increasing line has a positive slope and a decreasing line has a negative slope.
SolutionThe slope formula is given by
$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$.
With this we can determine the slopes of the given lines:
The red line:
You can read off the points $(1,2)$ and $(4,5)$:
$m=\frac{5-2}{4-1}=\frac{3}{3}=1$.
The blue line:
Here you can read off the points $(0,6)$ and $(1,3)$:
$m=\frac{3-6}{1-0}=\frac{-3}{1}=-3$.
The green line:
First, read off the points $(1,3)$ and $(4,3)$:
$m=\frac{3-3}{4-1}=\frac{0}{3}=0$.
The orange line:
The readable points are $(2,4)$ and $(4,3)$:
$m=\frac{3-4}{4-2}=\frac{-1}{2}=-0.5$.
-
Determine the slope of the lines given two points.
HintsUse the slope formula: $m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
Keep the order of subtraction in mind when using the slope formula.
Pay attention when subtracting negative numbers. Look at the example beside with the points $(-1,-1)$ and $(3,1)$.
SolutionThe slope formula is given by
$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
With this, we can determine the slopes of the given lines:
- $\mathbf{(3,1)}$ and $\mathbf{(5,7)}$ give a slope of $m=\frac{7-1}{5-2}=\frac{6}{3}=2$
- $\mathbf{(-1,7)}$ and $\mathbf{(3,5)}$ give a slope of $m=\frac{5-7}{3-(-1)}=\frac{-2}{4}=-0.5$
- $\mathbf{(4,3)}$ and $\mathbf{(3,4)}$ give a slope of $m=\frac{4-3}{3-4}=\frac{1}{-1}=-1$
- $\mathbf{(-1,-1)}$ and $\mathbf{(2,5)}$ give a slope of $m=\frac{5-(-1)}{2-(-1)}=\frac{6}{3}=2$
- $\mathbf{(2,2)}$ and $\mathbf{(4,9)}$ give a slope of $m=\frac{9-2}{4-2}=\frac{7}{2}=3.5$
-
Calculate the slope of the following situations.
HintsFor any two given points, use the slope formula:
$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
Pay attention to the order of subtraction when using the slope formula.
SolutionFirst, identify which value is independent (i.e. the $x$-axis) and which value is dependent (i.e. the $y$-axis).
Then, identify two points from the given information which we can use to plug into the slope formula,
$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
- Climber: $m=\frac{750-250}{7-2}=\frac{500}{5}=100$ feet per hour
- Mr. Miller: $m=\frac{450-0}{6-0}=\frac{450}{6}=75$ miles per hour
- Paul: $m=\frac{140-160}{10-0}=\frac{-20}{10}=-2$ lbs per week
- Luke: $m=\frac{27-25}{5-1}=\frac24=0.5$ dollars per day
-
Identify some points on the line.
HintsThe first coordinate of a point is the $x$-coordinate and the second is the $y$-coordinate.
Draw a line from the point parallel to the $x$-axis and read off the $y$-coordinate: this is where the line passes the $y$-axis.
Similarly, you get the $x$-coordinate.
SolutionTo get the coordinates of any point you proceed as follows:
- Draw a line from the point parallel to the x-axis and read off the y-coordinate: This is where the line passes the y-axis.
- Draw a line from the point parallel to the y-axis and read off the x-coordinate: This is where the line passes the x-axis.
- $(0,1)$
- $(2,2)$
- $(4,3)$
- $(8,5)$
-
Identify the equations for the given graphs in slope intercept form.
HintsFirst, you have to read off two points lying on the line.
Remember, the general form of a linear equation is $y=mx+b$.
You get the slope $m$ by using the slope formula,
$\quad~~~m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$.
The $y$-intercept $b$ is the point where the line intersects the $y$-axis.
- Increasing lines have a positive slope.
- Decreasing lines have a negative slope.
SolutionThe general form of a linear equation is $y=mx+b$.
- $b$ is the $y$-intercept, which is the point where the line intersects the $y$-axis.
- $m$ is the slope.
$m=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$.
Let's start with the green line and the points $(0,3)$ and $(2,7)$. We know from the point $(0,3)$ that $b=3$. Now we determine the slope:
$m=\frac{7-3}{2-0}=\frac{4}{2}=2$.
Thus we have the following equation: $y=2x+3$.
Now we take a look at the blue line and the points $(0,3)$ and $(2,0)$. Again we can read off $b=3$ directly. We still have to compute the slope:
$m=\frac{0-3}{2-0}=\frac{-3}{2}=-1.5$.
Together we get the equation: $y=-1.5x+3$.
The next one is the red line and the points $(0,2)$ and $(4,4)$. The first point with $x=0$ gives us $b=2$. Almost done: just the slope is left:
$m=\frac{4-2}{4-0}=\frac{2}{4}=\frac12$.
So we have that the equation is $y=0.5x+2$.
Last but not least, we have to handle the violet line and the points $(0,2)$ and $(4,-1)$. We can deduce from the point $(0,2)$ that $b=2$. So the slope is,
$m=\frac{-1-2}{4-0}=\frac{-3}{4}=-0.75$,
and the equation is given by: $y=-0.75x+2$.