Comparing Numbers Written in Scientific Notation


Basics on the topic Comparing Numbers Written in Scientific Notation
After this lesson you will be able to compare numbers written in scientific notation, using magnitude, decimals, and the laws of exponents.
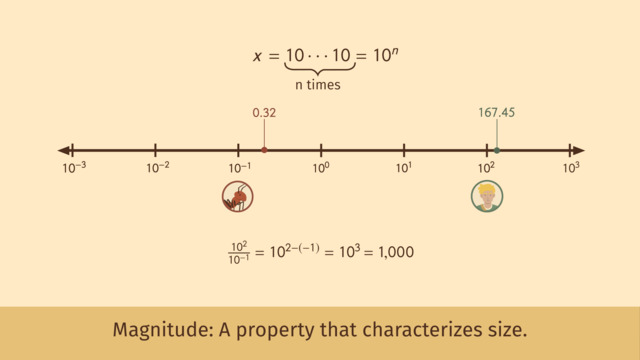
The lesson begins with a method for dividing out a common factor, in order to make a comparison between numbers written in scientific notation. It leads to a second method, which uses magnitude and exponents to make a comparison.
Learn how to compare numbers in scientific notation by helping Chad plan his interplanetary vacation!
This video includes key concepts, notation, and vocabulary such as: scientific notation (a mathematical expression which represents very large or very small numbers, by multiplying a decimal by a power of ten); the property of inequality (when two numbers in scientific notation have the same exponent, compare the decimals to find which is greater); and magnitude (the approximate size of a number, often written as a power of ten).
Before watching this video, you should already be familiar with scientific notation and basic arithmetic with numbers written in scientific notation.
After watching this video, you will be prepared to use scientific notation to solve higher-level mathematical problems.
Common Core Standard(s) in focus: 8.EE.A.4 A video intended for math students in the 8th grade Recommended for students who are 13-14 years old
Transcript Comparing Numbers Written in Scientific Notation
With billions and billions of possible planets to visit, planning a vacation can be quite confusing so many aliens get some guidance from this interstellar travel agency. It's run by Gladys Puffinsky, the planet pro. She knows the best vacation planets. Chad is here because he needs a break from his work at the gas station and wants to see more of his home galaxy. To pick the ideal destination, Chad will need to compare numbers in scientific notation. Gladys has two planets which she thinks are a perfect fit for Chad. Chad is worried about how crowded each planet will be so he asks Gladys: which planet has more inhabitants? On planet A there are 7.5 times 10 to the 9th inhabitants... and on planet B there are 5.2 times 10 to the 7th. How can we compare these numbers? Let's first take a look at the exponents notice they are different. One way to compare these numbers is to convert one of them so that the exponents are the same. Look at 7.5 times 10 to the 9th. Using the laws of exponents, we can write 10 to the 9th as the product of 10 to the 2nd and 10 to the 7th. That's 7.5, times 100, times 10 to the 7th which is equal to seven-hundred-fifty times 10 to the 7th. If we divide both sides by 10 to the 7th, we see that we are comparing seven-hundred fifty and five point two. We can see that seven hundred fifty is greater than five point two. Since we only divided by a positive number, the greater than or less than sign doesn't change. That means seven point five times ten to the ninth is greater than five point two times ten to the seventh. So it looks like planet A is more crowded than planet B but Chad isn't ready to decide yet. Since his home planet is bone dry, he wants to make sure there is plenty of water at his vacation spot. Gladys, which planet has more water? Planet A has 3.6 times 10 to the 20th gallons of water... and planet B has 2.52 times 10 to the 20th. Notice that these two numbers are in scientific notation. We can see this because each decimal part consists of a non-zero leading digit followed by a decimal. In this case, each decimal part is multiplied times ten to the 20th. Because the exponents are already the same here, we can just compare the decimal parts. Which is greater, 3.6 or 2 point fifty-two? Although 2 point fifty-two has more digits, 3.6 is the bigger number. Writing 3.6 as 3 point sixty makes that a little clearer. Three point six times 10 to the twentieth is greater than 2 point fifty-two times ten to the twentieth. So Chad knows planet A is wetter and more crowded than planet B. Hmm, that hasn't made the decision any easier. Chad always wears a baseball cap, so to feel right at home he'd ideally visit a planet with people who do the same! On planet A there are 3 times 10 to the 5th baseball cap wearers, and on planet B there are four point twenty one times 10 to the 7th. These numbers are in scientific notation, and have different exponents, so we have two options here. One option is to convert one of these numbers like before, so that the exponents are the same, then compare the decimal parts. But because these two numbers are in scientific notation, we can also just compare their magnitudes to determine which is bigger. The exponents of each are an expression of magnitude. Let's compare the exponents 5 and 7. Since 5 is less than 7...3 times 10 to the 5th is less than 4.21 times 10 to 7th. Remember, this only works when the numbers are in scientific notation. That means there are more baseball cap wearers on planet B than on planet A. Of course, Chad needs to think carefully before he makes this big decision. While he does that, let's review the ways we can compare numbers in scientific notation. If we encounter two numbers with different exponents we have two options. We can modify one of the numbers until both have the same exponent and then compare the decimal parts. Or, we can just compare the magnitudes directly, by comparing the exponents. The number with the greater exponent is bigger. If we encounter numbers with the same exponent we compare their decimal parts to see which is greater. When comparing decimal parts, the length is irrelevant. Sometimes, the shorter number is the greater number. Be sure that your numbers are in scientific notation before using these techniques. After careful consideration, Chad chooses planet B. He sure is excited about his upcoming vacation! Gladys, how much will this vacation cost? Hmm, looks like Chad is going to have to sell a lot more gas if he's going to be able to afford that.