What is a Function? The Difference between Functions and Relations


Basics on the topic What is a Function? The Difference between Functions and Relations
A relation is a way of expressing a connection or relationship between any two pieces of information.
A function is a particular kind of relation between sets. A function takes every element x in a starting set, called the domain, and tells us how to assign it to exactly one element y in an ending set, called the range.
For example, each person is in the following table is paired with a number representing his or her height:
Alex → 180 Claudia → 165 Gilbert → 204 Judith → 165
The given relation {(Alex, 180), (Claudia, 165), (Gilbert, 204), (Judith, 165)} is a function as every person is pairs with exactly one number, their height. The domain is (Alex, Claudia, Gilbert, Judith). The range is (165, 180, 204).
Remember that all functions are relations, but not all relations are functions. For instance, matching a person’s age with their height does not give a function: Say Claudia and Gilbert are both 15. In this case, 15 would get paired with both 165 and 204, meaning that every age is not paired with exactly one height.
Understand the concept of a function and use function notation. CCSS.MATH.CONTENT.HSF.IF.A.1
Transcript What is a Function? The Difference between Functions and Relations
Herman the German is at the end of his vacation in Japan, but he forgot to buy souvenirs! He decides to get a souvenir from one of the vending machines on one of the many touristy streets. Herman walks up to a pair of vending machines that look similar, but not exactly the same. The vending machines sell the same items and the keypads are the same.
Relations
Herman remembers that f(x) is math code for function notation and that the mark on the other vending machine is called a relation mapping diagram. What do functions and relations have to do with vending machines? Herman decides to go to the relation vending machine. He does feel lucky. Herman puts in 100 ¥. He chooses the Lap Pillow and enters E3 in the keypad.
What's happening? Why is the vending machine giving him a Noodle Eating Guard? that's also labeled E3? Upon closer inspection, Herman notices that there's something curious about this particular vending machine. There are several items that are labeled E3, there are also a few items labeled I3.
And look at that! S7 is the only item with that label. Herman decides to get a Rocketcroc Toaster. Again, he puts in money and enters in S7. Perfect! Herman decides to give the other items another try. After all, he does feel lucky! Once again, Herman puts in 100 ¥, chooses an item and enters the number in the keypad. This time, he chooses B3 since there are only two items labeled B3. Herman gets the square watermelon. Nice, but he wanted a Mommagotcha. So he tries again.
This time, he gets the Mommagotcha! But wait he didn't do anything differently, but got two different items. Herman thinks back to math class and remembers his teacher telling him that relations were when each element in the domain is related to one or more items in the range. When he enters in the code for an item, any one of the items with the same label could come out. With relations, an element in the domain of inputs can be related to one or more items in the range of outputs. Enough of this nonsense. Herman is pressed for time and he can't hope for a cool souvenir.
Functions
Herman decides to use the vending machine labeled with the function notation. Surely this will act like it should. Herman remembers that the function notation version of y = x is f(x) = x. And, although the name of this function is 'f', some other common letters used in function notation are 'g' or 'h', these would be read 'g' of 'x' and 'h' of 'x', respectively.
But no matter how a function is written, it has three main parts. First there is an input, 'x', that is chosen out of a set of starting points called the domain. Then, the function changes each input into a unique output, f(x), the artist formerly known as 'y'. The outputs create a set called the range.
Herman's sure he can get what he wants. He has his eye on AR2, which is the selfie stick. This'll make the perfect gift for his girlfriend! You've gotta be kidding the item's not coming out!
Herman's got an idea...Well, that didn't work. What's this? Herman catches a glimpse of a tool machine...Maybe...just maybe...NO...no...this is definitely worse.
What is a Function? The Difference between Functions and Relations exercise
-
Describe Herman's problems with the vending machine.
HintsEvery function is a relation, but not every relation is a function.
A function is a special kind of relation where for every input $x$ there is at most one output $y$.
SolutionHe puts 100 yen in the machine and inserts B3 for the Mammagotcha. But he gets a square melon instead.
That's because there are several items with the same label, like Mammagotcha and the square watermelon with B3. There is also a label with only one item: S7 and the rocket-toaster.
With relations, each element in the domain is related to one or more items in the range.
-
Explain the difference between functions and relations.
HintsThe following relation is a function:
you $\rightarrow$ number of brothers and sisters you have
The following relation is not a function:
you $\rightarrow$ the names of your brothers and sisters
Every function is a relation, but not the other way round.
SolutionBoth functions and relations have a set of inputs, called the domain, and a set of outputs, called the range.
For any relation, for each element of the domain you can have one or more elements in the range.
For a function, for each element of the domain you can have at most one element in the range.
-
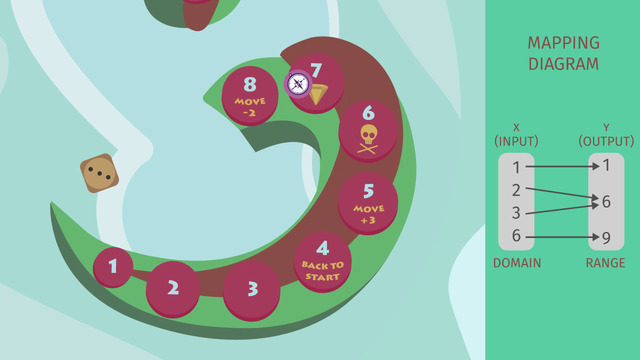
Decide which mapping diagrams represent a function.
HintsKeep the definition of a function in mind: for every element of the domain $x$ there exists at most one element in the range $y$ which is assigned to $x$.
You can imagine the definition of a function as follows: for each element in the domain there is at most one arrow.
If every $x$ in the domain is assigned to the same $y$, then the function is called a constant function.
Here is an example of a function:
SolutionThe kinds of diagrams we are looking at are called mapping diagrams. On the left of each picture we have the domain, the set of inputs, and on the right we have the range, the set of outputs.
If all inputs $x$ are assigned to at most one output $y$ then the mapping diagram in question is that of a function.
For any mapping diagram of a function, you see that only one arrow starts at any element of the domain. However many arrows lead to an element in the range doesn't matter.
Thus, from left to the right, we have a relation, a function, a function, a function, and a relation.
-
Identify which statements are describing a function.
HintsFor a function, we must have that each input $x$ is assigned at most one output $y$.
Remember the important facts about the town given above.
SolutionFor each house in town the address is uniquely assigned. Because of this, we can then view the assignment of addresses to houses as a function! This is how the postman knows where to deliver the mail.
Specifically, we have the function:
house $\rightarrow$ address,
where the address includes the street name, the house number, and the zip code.
If you leave out any of the three parts of the address, we don't have a function any longer, as the address no longer becomes unique. We know this from the given facts about the town.
For example:
- If we leave out the street name, then we know there exists more than one house with the number $30$ in town with the zip code 12345.
- If we leave out the house number, then we know there exists more than one house on a Beagle Street in the town with the zip code 12345.
- If we leave out the zip code, then we know there exists more than one house in town on Beagle Street with the house number 30.
-
Find three main facts about functions.
HintsEach element of the left set is assigned to one element of the right set.
The following is an example of a function:
you $\rightarrow$ your age.
Keep in mind that not every relation is a function. For example:
you $\rightarrow$ the names of all your friends.
SolutionThere are three main facts about functions:
- There is a set of all input values $x$, called the domain.
- A function $f(x)$ changes an input value $x$ into a unique output value $y$.
- The set of all output values $y$ is called the range.
-
Determine if the assignment is a function or relation.
HintsA person has a unique hair color but different people could have the same hair color.
For a function the assignment must be unique.
Here is an example for the difference between a relation and a function:
The assignment
Paul $\rightarrow$ date of his birthday
is unique and thus a function.
Turning this assignment around, we get
date $\rightarrow$ the person who was born on this date
which isn't unique at all.
Peter, Paul, and Mary drink just one soda each, but two of them could drink the same kind of soda.
SolutionThe difference of a relation and a function is the uniqueness of the assignment.
Hair color
Each person has a unique hair color, his own, so this assignment is a function. But the other way round you can surely find more than one person with the same color hair. Thus this is a relation.
Social security card
Each person has a unique the social security number. So this is a function.
Email
Paul has the email addresses paul_1@beagle.us, paul_2@dog.com, and paul_3@quitehungry.net. So three email addresses are assigned to Paul. This is a relation.
Soda
Each of the three drinks just one soda, so that's a function. Since two or three of them could order the same soda, this direction is just a relation.














LOL
"enough of this nonsense!" slayyyyy
bro got BOTH of his hands stuck :D