Inverse Functions

Basics on the topic Inverse Functions
A function takes every element x in a starting set, called the domain, and tells us how to assign it to exactly one element y in an ending set, called the range. Sometimes functions also have inverses. The inverse of a function f(x) is a function g(x) such that g(f(x)=x for any x in the domain of f(x).
For instance, the inverse of the function f(x)= (3/2) x + 2 is g(x)=(2/3) x - (4/3). Notice that g(f(x)) = g((3/2) x + 2) = (2/3)((3/2) x + 2) - (4/3) = ((2/3)(3/2) x + (2/3)*2) - (4/3) = (x + (4/3)) - (4/3) = x
How exactly did we find the inverse g(x) of f(x)? First we took f(x) = (3/2) x + 2.
Then we replaced f(x) with a variable y: y = (3/2) x + 2.
Then we switched all the x’s and y’s; so everywhere we saw a x, we replaced it with a y and everywhere we saw a y, we replaced it with an x: x = (3/2) y + 2.
We then isolated the y: x = (3/2) y + 2 x - 2 = (3/2) y 2x - 4 = 3y (2/3) x - (4/3) = y
Finally we replaced y with g(x) to get our inverse: g(x) = (2/3) x - (4/3).
Not every function has an inverse, for better or worse. You can check graphically if a function has an inverse function. Just as we can check if we have a function using the vertical line test, we can check if a function has an inverse function with the horizontal line test: if any horizontal line touches only one point of the graph, then an inverse function exists for the function which the graph represents.
It is interesting to notice that the function and its inverse graphically reflect each other on the coordinate system across the line x = y. Check it out with the example we computed above!
Build new functions from existing functions CCSS.MATH.CONTENT.HSF.BF.B.4
Transcript Inverse Functions
A not-so-long time ago, in a galaxy not too far away, two intrepid heroes are traveling across the universe. Hans Olus and his crew have received instructions on how to reach the inverse universe. Their instructions are in the form of a function; but, to get to the inverse universe, they need to find the inverse of the function. The crew can only initiate their ship's warp drive if the function and its inverse meet, so accuracy is paramount.
Inverse Functions
Some of the crew members do not know what an inverse function is, let alone how to find it. If you remember, for a function f(x), every ‘x’ value, produces one and only one ‘y’ value. Simply speaking, the inverse of a function is a way to “undo” a function. In other words, if you are given a 'y' value, an inverse function will give you back your original 'x' value. For every point, finding the inverse is easy. You just switch the positions of the ‘x’ and ‘y’ coordinates. So, for example, if we’re given the point 'P', (5, 3), the inverse of this point is P-1(3, 5). That was simple, but what about a function? Finding a function's inverse is just a tad bit trickier.
Vertical and Horizontal Line Test
First, you should know about the vertical line test. An equation is a function if it passes the vertical line test. Using a line parallel to the y-axis, if the line crosses the graph of your target equation at one and only one point for each 'x' value, then you can be sure the equation is a function. If an equation does not pass the vertical line test, then it is NOT a function.
Let's see if this equation passes the vertical line test. All linear equations, or equations with degree 1, pass the vertical line test. This linear equation is no different. It passes with flying colors. Now we can write this equation in function notation. In order to find out if the inverse of an equation also is a function, it has to pass the horizontal line test. Let's check this linear function to see if it'll pass. Yup! Looks good! So now we know that this function has an inverse function, but how do we find it?
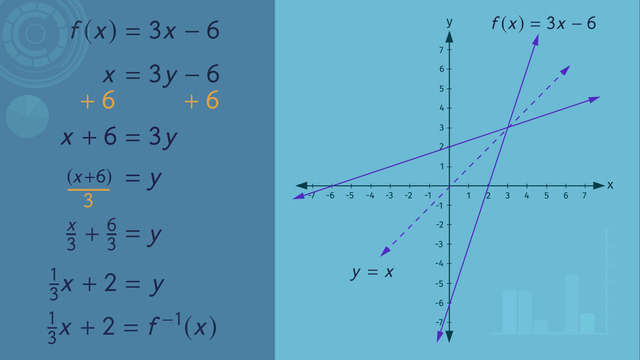
Finding the Inverse Function
We can do this algebraically by following some simple steps. Hans Olus and his crew have to find the inverse function of f(x) = 3x - 6. First, we'll put it into 'y =' notation. Next, we switch every 'x' in our original function with a 'y' and every 'y' with an 'x'. What happens next? You guessed it! We have to isolate 'y', just like we've done countless times before.
And there you have it, ladies and gentlemen! Our first inverse equation! There is an interesting fact about functions and their inverses. If y = x, you get the following graph. You will notice that the function and its inverse reflect about this line. Inverse functions are written using the following notation. This is read, "the inverse of F of X".
For our original equation, if we plug in values like 0, 1, 2, 3, 4 and so on we get the following values for 'y': If we plug these values into the inverse function we found, we should get back our original numbers. Let's do that now. The 'y' values for our original equation are -6, -3, 0, 3, and 6. Substituting these values into our inverse function we get...0, 1, 2, 3, 4! As you can see, the 'x' and 'y' values of the original and the inverse function are just interchanged.
Summary
To find the inverse function f-1(x) of a function f(x) you first have to replace f(x) with 'y' in the equation for f(x). Then you have to change all 'y's to 'x's and all 'x's to 'y's. Now you're ready to solve the equation for 'y'. Finally, replace the 'y=' notation with the inverse function notation, f⁻¹(x).
The crew pass their findings back to Hans Olus and he gets the warp drive ready to go to the parallel universe, Inversium. On no! What happened?! Seems like not only functions can have inverses in Inversium...
Inverse Functions exercise
-
Explain how to establish the inverse function.
HintsThe first step for finding the inverse function of $f(x)=x+5$ is:
$y=x+5$.
The next step is:
$x=y+5$.
Next, subtract $5$ to get $y=x-5$.
So $f^{(-1)}(x)=x-5$ is the inverse function of $f(x)=x+5$.
SolutionTo find the inverse function $f^{(-1)}(x)$ of a function $f(x)$, proceed as follows:
- Replace $f(x)$ with $y$ in the equation for $f(x)$.
- Interchange $y$ and $x$ in the equation.
- Solve the equation for $y$.
- Replace $y$ with $f^{(-1)}(x)$ in the resulting equation.
-
Find the inverse function of $f(x)=3x-6$.
HintsThe inverse of a given point $P(5,3)$ is $P^{-1}(3,5)$; just interchange $x$ and $y$.
The inverse function is like undoing the original function; you have to assign to each $y$ the corresponding $x$.
Let's look at another example: $f(x)=2x$:
- $y=2x$
- $x=2y$
- $y=\frac12x$
- $f^{(-1)}(x)=\frac12 x$
SolutionTo get the inverse function of $f(x)=3x-6$, we first replace $f(x)$ by $y$: $y=3x-6$.
Next we switch $x$ and $y$ to get $x=3y-6$.
We then solve this equation by isolating $y$:
$\begin{array}{rcl} x&=&3y-6\\ +6&&+6\\ x+6&=&3y\\ \color{#669900}{{~:3~}}&&\color{#669900}{{~:3~}}\\ \frac x3+\frac63&=&y\\ \frac13 x+2&=&y \end{array}$
Lastly, we replace $y$ by $f^{(-1)}(x)$ to get $f^{(-1)}(x)=\frac13 x+2$.
-
Verify that the following are inverses of each other.
HintsFor $x=2$, the function $y=2x+2$ gives us $2x+2=2 \cdot 2+2=6$.
For $x=6$, the function $y=\frac12 x-1$ gives us $\frac12 x-1=\frac12 6-1=2$.
If $g$ is the inverse of $y=2x+2$, then we have that the point $(12,g(12))=(12,5)$.
SolutionHere you see the value table for $y=\frac12x -1$ to the right.
We can quickly see that the columns of the table for $y=2x+2$ and the table for $y=\frac12x -1$ are interchanged.
This means that $y=2x+2$ and $y=\frac12x -1$ are inverses of each other!
$~$
Let's double-check:
- For $x=1$ we get $y=2\cdot 1+2=4$, and $y=\frac12\cdot 4-1=2-1=1$ gives us our $x$.
- For $x=2$, we get $y=2\cdot 2+2=6$, and $y=\frac12\cdot 6-1=3-1=2$ gives us our $x$.
- For $x=3$, we get $y=2\cdot 3+2=8$, and $y=\frac12\cdot 8-1=4-1=3$ gives us our $x$.
- For $x=4$ we get $y=2\cdot 4+2=10$, and $y=\frac12\cdot 10-1=5-1=4$ gives us our $x$.
- For $x=5$ we get $y=2\cdot 5+2=12$, and $y=\frac12\cdot 12-1=6-1=5$ gives us our $x$.
We can find the inverse of $y=2x+2$ algebraically as well:
- Interchange $x$ and $y$ to get $x=2y+2$.
- Solve $x=2y+2$ for $y$:
- Replace $y$ by $f^{(-1)}(x)$ to get the inverse function: $f^{(-1)}(x)=\frac12x-1$.
-
Determine the corresponding inverse function.
HintsUse the following steps:
- Replace $f(x)$ by $y$.
- Interchange $x$ and $y$.
- Solve the resulting equation for $y$.
- Replace $y$ by $f^{(-1)}(x)$.
Let's have a look at an example:
$\begin{array}{rcl} 3+y&=&x\\ -3&&-3\\ y&=&x-3 \end{array}$
SolutionTo find an inverse function just follow these steps:
- Replace $f(x)$ by $y$.
- Interchange $x$ and $y$.
- Solve the resulting equation for $y$.
- Replace $y$ by $f^{(-1)}(x)$.
Function 1: $f(x)=\frac12x-2$
- $y=\frac12x-2$
- $x=\frac12y-2$
- Adding $2$ leads to $x+2=\frac12y$ and multiplying with $2$ gives us $2x+4=y$.
- $f^{(-1)}(x)=2x+4$
- $y=\frac13x+1$
- $x=\frac13y+1$
- Subtracting $1$ leads to $x-1=\frac13y$ and multiplying with $3$ gives us $3x-3=y$.
- $f^{(-1)}(x)=3x-3$
- $y=-2x+4$
- $x=-2y+4$
- Subtracting $4$ leads to $x-4=-2y$ and dividing by $-2$ gives us $-\frac12x+2=y$.
- $f^{(-1)}(x)=-\frac12x+2$
- $y=5x-5$
- $x=5y-5$
- Adding $5$ leads to $x+5=5y$ and dividing by $5$ gives us $\frac15x+1=y$.
- $f^{(-1)}(x)=\frac15x+1$
-
Discuss how to decide if a relation is a function.
HintsEither of the line tests, vertical or horizontal, asks if any line parallel to one of the coordinate axis has only one point in common with the graph in question.
The difference between any relation and a function is the uniqueness of the $y$-value assigned to $x$.
The inverse function must be a function as well.
SolutionKeep in mind, that not every relation is also a function.
How can we decide if the graph of a relation is also graph of a function?
Use the vertical line test: if each line parallel to the $y$-axis has at most one point in common with the graph, then each $x$ is assigned to exactly one $y$ and we have a function. Otherwise, we don't have a function.
Is it also possible to check if a function is invertible?
Of course! You use the horizontal line test. If each line parallel to the $x$-axis has only one point in common with the graph, then there exists an inverse function.
-
Establish the corresponding inverse function.
HintsFirst replace $f(x)$ by $y$.
Then interchange $x$ and $y$ and solve the resulting equation for $y$.
Lastly, replace $y$ by $f^{(-1)}(x)$.
The sign of the slope of a function and its inverse is the same.
SolutionAll of the functions we are trying to find the inverse of are linear, so they are of the form $y=mx+b$. Keeping this in mind we can solve for each inverse by doing the following:
- Replace $f(x)$ by $y$. This gives us $y=mx+b$.
- Interchanging $x$ and $y$ leads to $x=my+b$.
- Solve $x=my+b$ for $y$ to get $y=\frac{x}{m}-\frac{b}{m}$.
- Replace $y$ by $f^{(-1)}(x)$ to get the inverse function $f^{(-1)}(x)=\frac{x}{m}-\frac{b}{m}$.
Function 1: $f(x)=-\frac12x+3$
- $m=-\frac12$
- $b=3$
- $f^{(-1)}(x)=\frac 1{-\frac12} x-\frac 3{-\frac12}=-2x+6$
- $m=-2$
- $b=3$
- $f^{(-1)}(x)=\frac 1{-2} x-\frac 3{-2}=-\frac12x+\frac32$
- $m=-3$
- $b=-2$
- $f^{(-1)}(x)=\frac 1{-3} x-\frac {-2}{-3}=-\frac13x-\frac23$
- $m=\frac14$
- $b=-1$
- $f^{(-1)}(x)=\frac 1{\frac14} x-\frac {-1}{\frac14}=4x+4$
- $m=-\frac13$
- $b=2$
- $f^{(-1)}(x)=\frac 1{-\frac13} x-\frac 2{-\frac13}=-3x+6$















Good job on it
Very well explained, but why do so many videos have to do with monsters, magic, aliens strenge galaxies and so on?
Very cool!