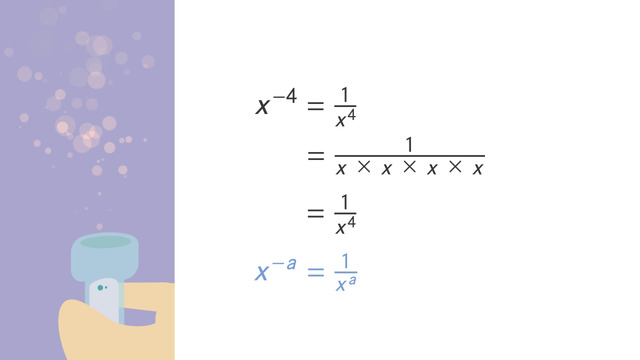Operations with Numbers in Scientific Notation
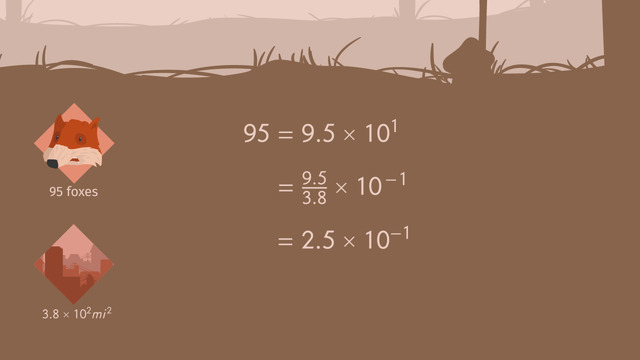

Basics on the topic Operations with Numbers in Scientific Notation
When dealing with numbers that are either very large or extremely small, knowing how to rewrite, and perform operations with, numbers in scientific notation can make handling such large or small numbers so much easier. The associative property and operations on exponents especially help when performing operations with numbers in scientific notation.
When multiplying numbers in scientific notation, like (a∙10m)∙(b∙10n), we can use the associative property to rewrite our multiplication, like (a∙b)∙(10m∙10n). The product (a∙b) is the product of two integers, and the product (10m∙10n), since they have the same base 10, will just follow the product property of exponents: (10m∙10n) = 10m+n. If the product c = (a∙b) is NOT greater than or equal to 1 and less than 10, then the answer c∙10m+n must be rewritten in scientific notation by moving the decimal point of c in the appropriate direction and adding or subtracting the appropriate amount from the exponent of 10m+n.
When dividing numbers in scientific notation, like (a∙10m)÷(b∙10n), we will also use the associative property to rewrite our operation, like (a÷b)∙(10m÷10n), where (10m÷10n) can be further simplified using the quotient property of exponents: (10m÷10n) = 10m-n. So we will then have (a÷b)∙(10m÷10n)=(a÷b)∙(10m-n). Again, we must have that (a÷b) is greater than or equal to 1, and less than 10.
Having the ability to perform operation with numbers in scientific notation will be like having a superpower in any scientific situation. Whether is is making calculations on Mars, measuring the effects of earthquakes, or just being in a lab, looking through a microscope.
Work with radicals and integer exponents. CCSS.MATH.CONTENT.8.EE.4
Transcript Operations with Numbers in Scientific Notation
Mr. and Mrs. Fox, who live in a village, need a new home. So they hire a real estate agent to help them. The agent only has listings of foxholes that are located in a nearby town. But the Foxes don't want to live in town because Mr. Fox thinks it will be crowded. He’s an artist, and he needs lots of space to work on his paintings, but with the addition of many baby foxes, they're practically bursting out of their current situation, so they can’t be too picky.
The real estate agent assures them that, although the new foxhole is located in town, it’s really nice and very family friendly. The real estate agent also tells them that the village where they currently live has population density of 750 foxes per mi.² and is much more crowded than the town. Mr. and Mrs. Fox are not so easily convinced of this, so they ask exactly how many foxes live in their area?
Calculating the Population
To calculate this information, we have to multiply the density by the area. First, write the population density in scientific notation, and then multiply the density times the area. To do this, we can apply the Commutative Property and rearrange the equation. Ok, that looks easier to manage. Order matters, so first calculate the product of 10² x 10³. Since the bases are the same, we can just add the exponents, so that’s equal to 10⁵. Next, multiply the coefficients together. 7.5(3.2) = 24, so you can write the equation as 24 x 10⁵, or you can write it in scientific notation as 2.4 x 10⁶, or you can write it in standard form as 2,400,000. 2,400,000 – that’s a lot of foxes.
Calculating the Population Density
To persuade the foxes to buy the foxhole that's located in the town, the real estate agent bombards them with facts and figures. He tells them the town has an area of 3.8 x 10² mi.². Although he’s sold apartments to 95 foxes so far, there's still lots of space, but they should move quickly before the best locations are sold. He tells the Foxes that to understand what a good deal the new foxhole is, they should calculate the population density of the town. Let's help the Foxes.
To do this, first write the population in scientific notation. 95 = 9.5 x 10¹ to find the polulation density, divide the population by the area.
Now rewrite the equation to make it easier to solve. That's better. Remember, order matters, so first simplify the exponents. When you divide bases raised to an exponent – subtract, this means subtract the exponent in the numerator from the exponent in the denominator: 1 - 2. now, divide the coefficients. Now we can write the equation in scientific notation: 2.5 x 10⁻¹
Since the exponent is negative, to write the number in standard form, move the decimal to the left one place value. The polpulation density of the nearby town is 0.25 foxes per square mile. Convinced the town is a good alternative to the village, the fox family packs up and moves. Although they have lots of space, the real estate agent forgot to mention just one small, but very important fact...
Operations with Numbers in Scientific Notation exercise
-
Calculate the fox population of Mr. and Mrs. Fox's village.
HintsThe commutative property of multiplication states that you can change the order of multiplication: $a\times b=b\times a$.
An example for multiplying powers with the same base is: $2^3\times 2^4=2^{(3+4)}=2^7$
The format of scientific notation is given by
$n\times 10^a$,
where $1\le n<10$, $n$ is the coefficient, $10$ the base, and $a$ the exponent.
SolutionMr. and Mrs. Fox are living in a village and they need a new home for their large family. They hire a real estate agent to help them, and the agent tries to convince them to move into town! But they aren't convinced that they should, as it sounds like the town will be too crowded for them.
The agent tells them that their current village has a fox density of 750 foxes per square mile. To calculate the fox population of their village we have to multiply the fox density with the area of the village.
First we write the fox density and the area of their village in scientific notation:
- The densitiy: $7.5\times 10^2$ foxes / mi$^2$
- The area: $3.2\times 10^3$ sqm
$(7.5\times 10^2)\times (3.2\times 10^3)$.
Next we use the commutative property the rearrange the multiplication
$(7.5\times 10^2)\times (3.2\times 10^3)=7.5\times 3.2\times 10^2\times 10^3$.
The decimal powers have the same base, so we add the exponents:
$7.5\times 3.2\times 10^2\times 10^3=7.5\times 3.2\times 10^{(2+3)}=7.5\times 3.2\times 10^5$.
Finally we multiply $7.5\times 3.2=24=2.4\times 10$ and add the exponents of the decimal powers once again to get
$7.5\times 3.2\times 10^5=2.4\times 10\times 10^5=2.4\times 10^6$.
We can then conclude that two million four hundred thousand foxes are living in their village.
-
Find the fox density of the town.
HintsThe format of scientific notation is given by
$n\times 10^a$,
where $1\le n<10$, $n$ is the coefficient, $10$ the base, and $a$ the exponent.
To divide powers with the same base just subtract the exponents, just as in this example:
SolutionWith the number of foxes and the area of the town, we can determine the density by dividing the number of foxes by the area.
$~$
First, write the number of foxes in a scientific notation:
$\large {95=9.5\times 10^1}$.
$~$
Then we divide the number of foxes by the area to get
${\large \frac{9.5\times 10^1}{3.2\times 10^2}=\frac{9.5}{3.8}\times\frac{10^1}{10^2}}$.
$~$
To divide two decimal powers, we subtract the exponents:
${\large \frac{9.5}{3.8}\times\frac{10^1}{10^2}=\frac{9.5}{3.8}\times 10^{(1-2)}=\frac{9.5}{3.8}\times 10^{-1}}$.
$~$
Lastly we divide $\frac{9.5}{3.8}=2.5$, and get the density of the town is $2.5\times10^{-1}=0.25$ foxes/mi$^2$.
-
Determine the fox population in Norway.
HintsThe commutative property of multiplication states that you can change the order of multiplication: $a\times b=b\times a$.
To multiply two numbers in scientific notation, just add the exponents of the decimal powers.
Here you see an example of multiplying two numbers written in scientific notation:
SolutionLet's figure out the population of Mr. Arctic-Fox's village in Norway.
Mr. Arctic-Fox says that 15 foxes per mi$^2$ live in an area of $4.5\times 10^3$ sqm.
We have to multiply the fox density by the area of the village, with both fox density and area expressed in scientific notation. We have: $(1.5\times 10^1)\times (4.5\times 10^3)$.
Using the commutative property of multiplication, we can rearrange our calculation to get
$(1.5\times 10^1)\times (4.5\times 10^3)=1.5\times 4.5\times 10^1\times 10^3$.
We can multiply the decimal powers with the same base by adding the exponents:
$1.5\times 4.5\times 10^1\times 10^3=6.75\times 10^4$.
So the population of Mr. Arctic-Fox's village is thus $6.75\times 10^4=67500$.
-
Examine the different population densities.
HintsYou have to divide the population by the area to get the density.
The format of scientific notation is given by
$n\times 10^a$,
where $1\le n<10$, $n$ is the coefficient, $10$ the base, and $a$ the exponent.
To divide decimal powers just subtract the exponents, like in the following example:
SolutionThe population density is the population in an area. Thus we have to divide the population by the area each time:
$~$
Wolves:
$\begin{array}{rclll} \frac{240}{300}&=&\frac{2.4\times 10^2}{3.0\times 10^2}\\ &=&\frac{2.4}{3.0}\times\frac{10^2}{10^2}&|&\text{subtract the exponents}\\ &=&0.8\times 10^{(2-2)}\\ &=&0.8\times 10^0\\ &=&8.0\times 10^{-1} \end{array}$
Deers:
$\begin{array}{rclll} \frac{230}{400}&=&\frac{2.3\times 10^2}{4.0\times 10^2}\\ &=&\frac{2.3}{4.0}\times\frac{10^2}{10^2}&|&\text{subtract the exponents}\\ &=&0.575\times 10^{(2-2)}\\ &=&0.575\times 10^0\\ &=&5.75\times 10^{-1} \end{array}$
Boars:
$\begin{array}{rclll} \frac{130}{125}&=&\frac{1.3\times 10^2}{1.25\times 10^2}\\ &=&\frac{1.3}{1.25}\times\frac{10^2}{10^2}&|&\text{subtract the exponents}\\ &=&1.04\times 10^{(2-2)}\\ &=&1.04\times 10^0 \end{array}$
Rabbits:
$\begin{array}{rclll} \frac{420}{300}&=&\frac{4.2\times 10^2}{3.0\times 10^2}\\ &=&\frac{4.2}{3.0}\times\frac{10^2}{10^2}&|&\text{subtract the exponents}\\ &=&1.4\times 10^{(2-2)}\\ &=&1.4\times 10^0 \end{array}$
-
Decide which numbers are written in scientific notation.
HintsKeep the definition of scientific notation above in mind.
The number $2016$ written in scientific notation is
$2016=2.016\times 10^3$.
SolutionThe fox density is given by $750$ foxes / mi$^2$.
To write $750$, or $750.0$, in scientific notation, we move the decimal place over two to the left to get $750=7.5\times 10^2$.
Remember that we do this as $n$ must be greater than or equal to $1$ and less than $10$.
The area of of the village, $3.8\times 10^3$, is already given in scientific notation.
We can also write $7.5\times 3.8=24$ in scientific notation: $24=2.4\times 10^1$.
-
Complete the following operations using scientific notation.
HintsKeep in mind that $1\le n<10$.
To multiply (or divide) decimal powers, just add (or subtract) the exponents.
Take a look at the following example:
SolutionTo multiply (or divide) numbers in scientific notation, first group like terms and then multiply (or divide) the like terms.
To multiply (or divide) the decimal powers we add (or subtract) the exponents.
Remember: if the product of the coefficients is not greater than or equal to $1$ and less than $10$, then we have to also write this number in scientific notation.
$~$
Problem 1:
$\begin{array}{rcl} 1.2\times 10^3\times 3.2\times 10^4&=&1.2\times 3.2\times 10^3\times 10^4\\ &=&3.84\times 10^7 \end{array}$$~$
Problem 2:
$\begin{array}{rcl} {\large \frac{1.44\times 10^{\large 4}}{1.2\times 10^{\large 5}}}&=& {\large \frac{1.44}{1.2}}\times{\large \frac{10^{\large 4}}{10^{\large 5}}}\\ &=&1.2\times 10^{-1} \end{array}$$~$
Problem 3:
$\begin{array}{rcl} 3.55\times 10^2\times 4.2\times 10^3&=&3.55\times 10^2\times 4.2\times 10^3\\ &=&14.91\times 10^5\\ &=&1.491\times 10^6 \end{array}$$~$
Problem 4:
$\begin{array}{rcl} {\large \frac{6.75\times 10^{\large 7}}{1.5\times 10^{\large 5}}}&=&{\large \frac{6.75}{1.5}}\times{\large \frac{10^{\large 7}}{10^{\large 5}}}\\ &=&4.5\times 10^2 \end{array}$