Exponential Growth and Decay

Basics on the topic Exponential Growth and Decay
Imagine you have a material, like gold or kryptonite, and you have to find out the amount of that material you have after a given percentage of change, after a certain period of time. Instead of doing multiple and repetitive multiplications and additions, there is a shorter and easier way to do it, using the formulas for exponential growth and decay.
The standard formula for exponential growth is X_t = X_0(1 + r)t/n, where: t is the period of time, expressed in units of time, X_t is the amount after the period of time t, X_0 is the original size or amount, r is the rate of growth, also called growth factor, n is the time needed for 1 growth factor.
Likewise, the standard formula for exponential decay is X_t = X_0(1 - r)t/n, where r is now the rate of decay, which is why it is being subtracted now instead of added.
Lets look at an example: a certain culture with 10,000 microorganisms in a petri dish were seemed to be increasing in quantity by 10% after 3 seconds. We can use the formula for exponential growth to find out how many organisms will be in the petri dish after 30 seconds. To do this we first see that X_0 = 10000, r = 10% or 0.1, t = 30 days, and n = 3 days
So, X_30 = 10000 * (1 + 0.1)30/3 X_30 = 10000 * (1.1)10 X_30 = 10000 * 2.5937 X_30 = 25,937 microorganisms
Knowing how to compute exponential growth and decay can be useful when you find yourself working in laboratory research, banking and financial analysis, and even agriculture and tech fields that require the use of meaningful statistics. These formulas then become powerful tools, in some sense, for predicting the future.
Analyze functions using different representations. CCSS.MATH.CONTENT.HSF.IF.C.8.B
Transcript Exponential Growth and Decay
The largest longhorn breeder’s competition is coming up and Old MacDonald is tired of coming in second place. His wife, Mrs. MacDonald, suggests that Old MacDonald create a formula using exponential growth and decay to feed his favorite longhorn, BEVO, so that his horns grow faster.
Exponential Growth
Old MacDonald's wife reminds him that the standard form of a growth equation is: x_t = x_0 * (1 + r)t/n and to be very careful with his calculations. 't' is the time in days, so ‘x sub t’ is the final size after ‘t’ days. ‘x naught’ is the original size, (1 + r) is the growth factor, where '1' represents 100%, and ‘n’ is the time it takes for the horns to grow by a full growth factor.
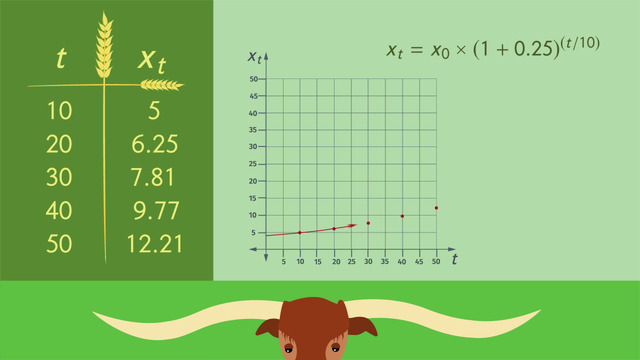
Old MacDonald comes up with a special vitamin mix that promises a horn growth of 25%, which can be written as 0.25, every 10 days. So the formula is: x_t = x_0 * (1 + 0.25)t/10. The initial length of BEVO’s horns, 'x naught', is 4 feet. In order to know how fast BEVO’s horns will grow, Old MacDonald plugs in the number of days for ‘t’. So, after 10 days, the equation for how long BEVO’s horns will be is 4 * (1.25)(10/10) feet, or simply, 5 feet.
Every day for 50 days, Old MacDonald plans to feed BEVO meals with specially-prepared vitamins mixed in. Let’s take a look at how much BEVO’s horns will grow: After 10 days, BEVO’s horns will be 5 feet long. After 20 days, they will be 6.25 feet long, and after 50 days, BEVO’s horns will be about 12.21 feet long and BEVO will be assured to win the competition!
Exponential Decay
BUT Old MacDonald makes a SLIGHT calculation error and writes 2.5 instead of 0.25. After just 20 days, BEVO’s horns are already at 49 feet! Since Old MacDonald isn’t allowed to enter a longhorn with horns longer than 12.5 feet into the competition, he has to reverse the process. But he only has 30 days left in which to do so. Old MacDonald’s wife helps him again and tells him that the equation for decay is similar to the equation for growth, BUT instead of adding 1 and 'r' to get the growth factor, 'r' is subtracted from 1 to get the decay factor.
Old MacDonald wants to have BEVO's horns close to 12.5 feet, so he concocts another vitamin mix that has a decay factor of 37%, which means that every 10 days, BEVO's horns will shrink by 37%.
BEVO's horns currently measure 49 feet from tip to tip. Let’s take a look at the length of the horns after 10 days and see if this new pill will fix Old MacDonald’s problem. After 10 days, BEVO’s horns should be 30.87 feet long; after 20 days, about 19.45 feet and 12.25 feet after 30 days.
It’s the day of the longhorn breeder’s competition! Old MacDonald is so excited! WHAT’S THIS!?!? I guess you could say Old MacDonald is “stumped” as to how this happened…
Exponential Growth and Decay exercise
-
Define exponential growth and decay.
HintsJust look at the basis of the power:
- $1+r>1$
- $1-r<1$
If you raise a number greater than $1$ by a positive power you get a value greater than $1$ as well.
Look at the example, consider $x_t=10\times 1.5^{t}$.
Here we have
- $x_1=15$
- $x_2=22.5$
- ...
SolutionHere you see the formula for an exponential process. We distinguish between exponential growth and exponential decay.
Let's have a look at the basis of the power, $(1\pm r)$. What does this mean?
For $(1+r)$ we have a basis greater than $1$ and thus a power which is greater than $1$ as well. So $x_t$ is bigger than $x_0$. We can then conclude that we have an exponential growth. $(1+r)$ is called the growth factor.
By the same argument we can determine an exponential decay for $(1-r)$. Here $(1-r)$ is called the decay factor.
What's the meaning of the other terms? The other terms are independent of exponential growth or decay.
- $\frac tn$ is the growing (or decaying) time in days by one growth (or decay) factor.
- $x_t$ is the size after $t$ days.
- $x_0$ is the original size, the starting size.
-
Determine the growth of Bevo's horns.
HintsJust put the given value for $t$ in the growth formula.
To round a decimal number, like $3.1415$ for example, proceed as follows:
- Look at the third decimal position; e.g. $1$ for $3.1415$.
- If this is less than $5$ you have to round down.
- Otherwise you have to round up.
For $t=100$, we have
$x_{100}=4\times 1.25^{\large \left(\frac {100}{10}\right)}=37.2529...\approx 37.25$.
SolutionWe can see all solutions in the table to the right.
How do we get these solutions?
We put each $t$-value in the formula $x_t=4\times 1.25^{\large \left(\frac t{10}\right)}$:
- $t=10$ gives us $x_{10}=4\times 1.25^{\large \left(\frac {10}{10}\right)}=5$.
- $t=20$ gives us $x_{20}=4\times 1.25^{\large \left(\frac {20}{10}\right)}=6.25$.
- $t=30$ gives us $x_{30}=4\times 1.25^{\large \left(\frac {30}{10}\right)}=7.8125\approx 7.81$.
- $t=40$ gives us $x_{40}=4\times 1.25^{\large \left(\frac {40}{10}\right)}=9.765625\approx 9.77$.
- $t=50$ gives us $x_{50}=4\times 1.25^{\large \left(\frac {50}{10}\right)}=12.2070...\approx 12.21$.
-
Calculate the size of Bevo's horns.
HintsPut the given value for $t$ in the formula
$x_t=4\times (1+2.5)^{\large \left(\frac t{10}\right)}$.
Have a look at the following example for rounding $2.71828$:
- Look at the third decimal position; e.g. $8$.
- If this is less than $5$ you have to round down.
- Otherwise you have to round up.
For $t=60$:
$x_{60}=4\times 3.5^{\large \left(\frac {60}{10}\right)}=7353.0625...\approx 7353.06$.
SolutionTo get the values for $x_t$, put each $t$ into the formula $x_t=4\times 3.5^{\left(\frac t{10}\right)}$:
- $t=10$ gives us $x_{10}=4\times 3.5^{\large \left(\frac {10}{10}\right)}=14$.
- $t=20$ gives us $x_{20}=4\times 3.5^{\large \left(\frac {20}{10}\right)}=49$.
- $t=30$ gives us $x_{30}=4\times 3.5^{\large \left(\frac {30}{10}\right)}=171.5$.
- $t=40$ gives us $x_{40}=4\times 3.5^{\large \left(\frac {40}{10}\right)}=600.25$.
- $t=50$ gives us $x_{50}=4\times 3.5^{\large \left(\frac {50}{10}\right)}=2100.875\approx 2100.88$.
-
Decide if either exponential growth or decay is given.
HintsThe factor for exponential decay (or growth) is less than (or greater than) $1$.
If we have a growth of $30\%$, we get the following growth factor: $1+30\%=1+0.3=1.3$.
SolutionFor all the examples above we have to determine the growth, or decay, factor as well as the original size $x_0$.
Water lilies - an exponential growing process:
- $1+r=1+0.2=1.2$
- $x_0=2$
- $x_t=2\times 1.2^t$, where $t$ stands for the time in months.
- $1-r=1-0.15=0.85$
- $x_0=2$
- $x_t=2\times 0.85^t$, where $t$ stands for the time in years.
- $1-r=1-0.2=0.8$
- $x_0=2$
- $x_t=2\times 0.8^t$, where $t$ stands for the time in $10$ years.
- $1+r=1+1=2$
- $x_0=2$
- $x_t=2\times 2^t$, where $t$ stands for the time in periods.
-
Establish the formula for Bevo's shrinking horns.
HintsWhat's the meaning of the terms in the formula?
- $\frac tn$ is the decaying time by one decay factor in days.
- $x_t$ is the size after $t$ days.
- $x_0$ is the original size, the starting size.
Keep in mind that you have to subtract the decay rate from $1$.
Distinguish between the original size, that's the size at the beginning, and the size at $t$, which must be smaller than the original size.
SolutionWe already know the formula for exponential decay, $x_t=x_0\times (1-r)^{\left(\frac t{10}\right)}$, so all we need to do is put in our known values.
The original size of the horns is 49 feet, so $x_0=49$.
The size at $t$ is unknown.
To get the decay factor we have to subtract the rate $r=0.37$ from $1$ to get $1-0.37=0.63$.
Putting all these values into the exponential decay equation, we get:
$x_t=49\times (1-0.37)^{\left(\frac t{10}\right)}=49\times 0.63^{\left(\frac t{10}\right)}$.
-
Decide the corresponding exponential function.
HintsPut in the corresponding $x$-value in the respective function equation.
You can find the starting value for each function; i.e. $f(0)$, $g(0)$, and $h(0)$.
Check each point $(x,y)$. It must satisfy either $y=f(x)$, $y=g(x)$, or $y=h(x)$.
SolutionTo check if any point belongs to a given function, put the $x$ value of the point into the function.
Let's start with $x=0$:
- $f(0)=3\times 1.2^0=3$ $\rightarrow$ $(0,3)$
- $g(0)=4\times 0.9^0=4$ $\rightarrow$ $(0,4)$
- $h(0)=5\times 0.5^0=5$ $\rightarrow$ $(0,5)$
- $f(4)=3\times 1.2^4\approx 6.2$ $\rightarrow$ $(4,6.2)$
- $g(4)=4\times 0.9^4\approx 2.6$ $\rightarrow$ $(4,2.6)$
- $h(4)=5\times 0.5^4\approx 0.3$ $\rightarrow$ $(4,0.3)$