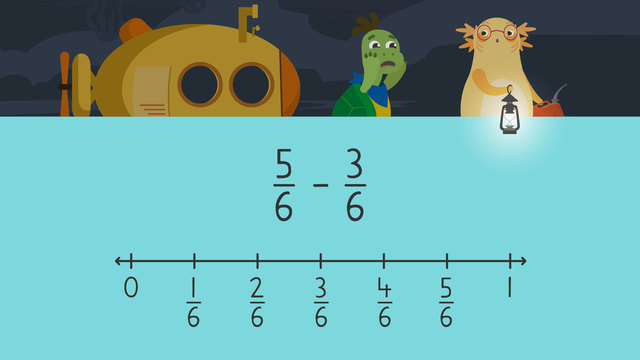Subtracting Fractions with Like Denominators
- Subtracting Fractions with Like Denominators
- Subtracting Fractions – Steps
- Subtracting Fractions – Example
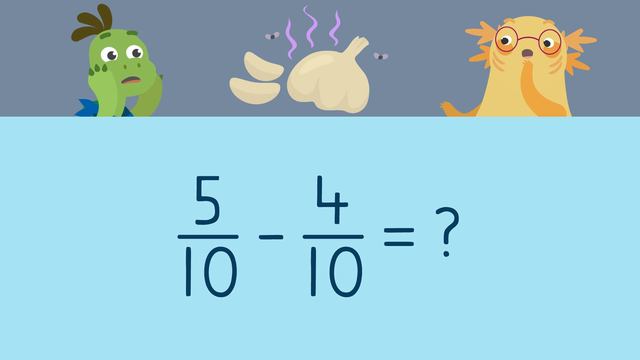

Basics on the topic Subtracting Fractions with Like Denominators
Subtracting Fractions with Like Denominators
What is subtracting fractions with common denominators? Subtracting fractions with same denominator is similar to subtraction with whole numbers, but instead we are subtracting simple fractions. When subtracting fractions with like or common denominators, there are some steps for subtracting fractions that need to be followed. What are the rules for subtracting fractions? In fact, the rules for adding and subtracting fractions are very similar, the only difference is the operation which in this case is subtraction.
Subtracting Fractions – Steps
| Step # | What to do |
|---|---|
| 1 | Check that the denominators are the same, and write it in the total. |
| 2 | Subtract the numerators. |
| 3 | Write the numerator above the denominator in the total. |
These steps are the rules for subtracting fractions with common denominators. Many have asked “when subtracting fractions do you subtract the denominator?” and the answer is no. The number of parts your whole is broken into does not change, so we never subtract the denominators when subtracting fractions with common denominators.
Subtracting Fractions – Example
Here are some examples for subtracting fractions with like denominators. Let’s take a look at an example of subtracting fractions with a same denominator. Here, we’ll subtract five-eighths minus two-eighths following the steps and rules for subtracting fractions with like denominators.
- Step 1: Check that the denominators are the same, and write it in the total
In this example, the denominators are eight, so the answer will have an eight as the denominator as well.
- Step 2: Subtract the numerators
Here, the numerators are five and two, so we subtract them.
- Step 3: Write the numerator above the denominator in the total
Five minus two is three, so the answer is three-eighths.
Subtracting Fractions with Like Denominators – Summary
If you forget what to do when subtracting fractions, always remember the steps for subtracting fractions that need to be followed. What are the rules for subtracting fractions? Below are the rules and steps to keep in mind when subtracting fractions with the same denominator.
- Step 1: Check that the denominators are the same, and write it in the total
- Step 2: Subtract the numerators
- Step 3: Write the numerator above the denominator in the total
Want some more subtracting fractions practice? In this video you can find subtracting fractions examples and on this website there are worksheets for subtracting fractions with denominators, along with other activities, and interactive exercises.
Transcript Subtracting Fractions with Like Denominators
Axel and Tank are using a magic recipe to make an invisible spray. "We're going to be mixing invisible ink, Joyful Unicorn Tears, and garlic." "Yeah, but there's just one problem..." "we have to subtract fractions in order to identify how much we need of each ingredient!" Let's help Axel and Tank by, "Subtracting Fractions with Like Denominators", so they can make invisible spray! A fraction describes a part of a whole OR (...) a part of a collection. The top number, or the NUMERATOR, represents how many equal parts of a whole we have. The bottom number, or the DENOMINATOR, represents how many equal parts our whole is divided into. (...) A COMMON or LIKE denominator refers to fractions (...) with the SAME denominators. To start, we will subtract five-eighths and two-eighths to see how much invisible ink they need. When you subtract fractions with LIKE denominators... the denominator ALWAYS stays the same since the number of parts in our whole does NOT change. That is why our first step is to double check that the denominators are the SAME. Since they are LIKE denominators we can write the denominator of our total HERE. The second step is to subtract the numerators. Five minus two is three, and we write it HERE. (...) Axel and Tank need three-eighths of a container of invisible ink. Next, they will use Joyful Unicorn Tears. To determine the amount of tears, we will solve nine-twelfths minus three-twelfths. What is the first step? (...) First, double check that the denominators are the same... and write it HERE. What is the second step? (...) The second step is to subtract the numerators. What is nine minus three? (...) Six, so the answer is six-twelfths... which can also be simplified to one half. Axel and Tank need one-half of a container of Joyful Unicorn Tears. Last, we will subtract five-tenths minus four-tenths to see how much garlic they need. This time, try subtracting on your own. Pause the video so you have time to work (...) and press play again when you're ready to see the steps for finding the answer! First, double check that the denominators are the same... and write ten HERE. Next, subtract five and four to get... one. Axel and Tank will use one-tenth of a garlic bulb to complete their recipe! Before we see if the invisible spray works, let's summarize. Remember, (...) when subtracting fractions with LIKE denominators... The first step is to "double check that the denominators are the same, and write it in the total". The second step is to "subtract the numerators". The third step is to write the numerator above the denominator, simplifying the fraction when you need to. Let's see if the invisible spray works! "Axel, I can't see you anymore (...) THIS IS AWESOME!" "Yeah! Wait (...) do you smell (...) garlic!?" "Ew gross!"
Subtracting Fractions with Like Denominators exercise
-
What are the steps to subtract like fractions?
HintsThe numerator is the top number in the fraction and the denominator is the bottom number.
To subtract fractions, they need to have the same denominator.
As long as fractions have the same denominator, their top numbers can be subtracted.
SolutionFirst, check that the denominators are the same and write it in the total.
- $\frac{5}{\textbf{8}} - \frac{3}{\textbf{8}} = \frac{}{\textbf{8}}$
- $5 - 3 = 2$
- * $\frac{5}{8} - \frac{3}{8} = \frac{\textbf{2}}{8}$
-
Which subtraction problems have like fractions?
HintsLike fractions have the same number in the denominator.
The denominator is the bottom number in the fraction.
SolutionLike fractions are fractions that have the same denominator, or bottom number. These problems have like fractions:
- $\frac{3}{4} - \frac{1}{4}$
- $\frac{2}{2} - \frac{1}{2}$
- $\frac{7}{8} - \frac{3}{8}$
- $\frac{3}{8} - \frac{3}{4}$
- $\frac{5}{6} - \frac{2}{3}$
- $\frac{2}{6} - \frac{2}{4}$
-
Which images model the subtraction problems?
HintsThe denominator is the total number of equal parts.
Count the number of shaded parts. This is the numerator.
SolutionFirst, look at the common denominator. That is the number of total pieces each rectangle is divided into.
Then, look at the numerators. That is the number of shaded parts of the rectangles.
2/3 - 1/3: each rectangle will have 3 parts. The first rectangle will have 2 shaded parts and the second will have 1 shaded part.
3/4 - 1/4: each rectangle will have 4 parts. The first rectangle will have 3 shaded parts and the second will have 1 shaded part.
5/6 - 2/6: each rectangle will have 6 parts. The first rectangle will have 5 shaded parts and the second will have 2 shaded parts.
5/8 - 2/8: each rectangle will have 8 parts. The first rectangle will have 5 shaded parts and the second will have 2 shaded parts.
-
Solve the subtraction problems.
HintsWhen subtracting like fractions, the denominator stays the same.
Subtract the numerators to find the new numerator.
SolutionWhen subtracting like fractions, find the solution by:
- Keeping the denominator the same
- Subtracting the numerators
$\frac{5}{6}$ - $\frac{3}{6}$ = $\frac{2}{6}$
$\frac{5}{8}$ - $\frac{1}{8}$ = $\frac{4}{8}$
$\frac{3}{4}$ - $\frac{2}{4}$ = $\frac{1}{4}$
-
Solve the subtraction problem using the model.
HintsFirst, check that the denominators are the same. Then, subtract the numerators.
- The numerator is the top number.
- The denominator is the bottom number.
SolutionFirst, check that the denominators are the same. They are both 8, so these fractions are like fractions.
Write 8 in the denominator of the total.
$\frac{7}{8} - \frac{5}{8} = \frac{?}{\textbf{8}}$
Next, subtract the numerators: 7 - 5 = 2.
Write 2 in the numerator of the total.
So, $\frac{7}{8} - \frac{5}{8} = \frac{\textbf{2}}{8}$.
-
Solve the subtraction problems and simplify.
HintsTo simplify, find a common factor of both the numerator and denominator. Then, divide both numbers by the common factor.
To subtract fractions with like denominators, keep the denominator the same and subtract the numerators.
SolutionFirst subtract the numerators and keep the denominators.
- For example, $\frac{5}{6} - \frac{2}{6} = \frac{3}{6}$.
- For example, both 3 and 6 are divisible by 3. So, $\frac{3}{6} = \frac{1}{2}$.
- $\frac{7}{8} - \frac{3}{8} = \frac{4}{8} \rightarrow \frac{4}{8} = \frac{\textbf{1}}{\textbf{2}}$
- $\frac{3}{4} - \frac{1}{4} = \frac{2}{4} \rightarrow \frac{2}{4} = \frac{\textbf{1}}{\textbf{2}}$
- $\frac{3}{3} - \frac{1}{3} = \frac{\textbf{2}}{\textbf{3}}$
- $\frac{5}{6} - \frac{1}{6} = \frac{4}{6} \rightarrow \frac{4}{6} = \frac{\textbf{2}}{\textbf{3}}$
- $\frac{3}{4} - \frac{2}{4} = \frac{\textbf{1}}{\textbf{4}}$
- $\frac{5}{8} - \frac{3}{8} = \frac{2}{8} \rightarrow \frac{2}{8} = \frac{\textbf{1}}{\textbf{4}}$
- $\frac{7}{8} - \frac{5}{8} = \frac{2}{8} \rightarrow \frac{2}{8} = \frac{\textbf{1}}{\textbf{4}}$